图源：文心一言

考研笔记整理~🥝🥝

在数据结构和算法中，查找是一种常见的操作，它的目的是在一个数据集合中找到一个满足条件的元素。本文将介绍三种常用的查找方法，分别是顺序查找、折半查找和分块查找~🥝🥝

第1版：查资料、写BUG、画配图~🧩🧩

参考用书：王道考研《2024年数据结构考研复习指导》

参考用书配套视频：7.1_查找的基本概念_哔哩哔哩_bilibili

协作： Chat GPT、BING AI、文心一言~

📇目录

🦮思维导图

🧵简介与对比

🌰举栗与代码

⌨️顺序查找

⌨️折半查找

⌨️分块查找

🔚结语

🦮思维导图

本篇仅涉及到顺序、折半、分块查找的代码；
思维导图为整理王道教材第7章查找的所有内容，其余学习笔记在以下博客~
- 🌸数据结构07：查找[C++][朴素二叉排序树BST]_梅头脑_的博客-CSDN博客
- 🌸数据结构07：查找[C++][平衡二叉排序树AVL]_梅头脑_的博客-CSDN博客
- 🌸数据结构07：查找[C++][红黑二叉排序树RBT]_梅头脑_的博客-CSDN博客
- 🌸数据结构07：查找[C++][B树Btree]_梅头脑_的博客-CSDN博客

🧵简介与对比

数据结构中有一个常见的问题，就是如何在一个数据集合中查找一个特定的元素。这个问题有不同的解决方法，其中比较常用的是顺序查找、折半查找和分块查找。

那么，它们有什么区别呢？

顺序查找：它对顺序表和链表都是适用的。对于顺序表，可通过数组下标递增来顺序扫描每个元素；对于链表，可通过指针next来依次扫描每个元素。
折半查找：仅适合有序的顺序表。首先比较给定值Key与中间位置元素的关系，若不相等，可以从中间元素以外的前半部分或者后半部分查找，重复此步骤直到找到指定元素或查找失败。
分块查找：适合索引表有序的顺序表和链表，尤其是链表可以较为方便地实现动态查询（就是允许数据的插入和删除），当然如果需要频繁地查找还是推荐树形结构。查询方式：在索引表中确定待查记录所在的块，可以顺序查找或是折半查找；(2)在块内顺序查找。

三种表的区别如下——

查找方式	适用数据类型	数据要求	搜索范围缩小速度	平均比较次数	额外空间开销
顺序查找	顺序表、链表	无要求	较慢	成功：(n+1)/2 失败：n+1	0或1
顺序查找	顺序表、链表	数据有序	较慢	成功：(n+1)/2 失败：n/2+n/(n+1)	0或1
折半查找	顺序表	数据有序	快速	成功：log(n+1)-1	0或1
分块查找	顺序表、链表	索引表有序块间可无序	快速	表顺序+块顺序： (b+1)/2+(s+1)/2	需要额外空间存储索引表
分块查找	顺序表、链表	索引表有序块间可无序	快速	表折半+块顺序： log(b+1)+(s+1)/2	需要额外空间存储索引表

备注

顺序、折半查找额外空间开销，实际上可能近似于0；不过有些大佬习惯将需要比较的元素放置在数组的0位，或者将需要查找的数放在内存中也算作1位~
平均查找次数概念如下，在博文的后面会举栗说明：

成功平均查找次数：Σ(查找第i个元素概率x找到第i个元素所需的比较次数）；
失败平均查找次数：Σ(第i个位置查找失败概率x找到第i个位置所需的比较次数）。

🌰举栗与代码

⌨️顺序查找

一般也可分为无序表的查找与有序表的查找，查找过程简而言之就是从头到尾查找。无序、有序两种表的差别仅体现在查找失败部分：

无序表查找失败：从头查到尾；
有序表查找失败：如果【当前查找的数字index < 数组的下一个数字target】，则停止查找~

以此数组为例{7,10,13,16,19,29,32,33,37,41,43}，分别查找11、32，如图所示：

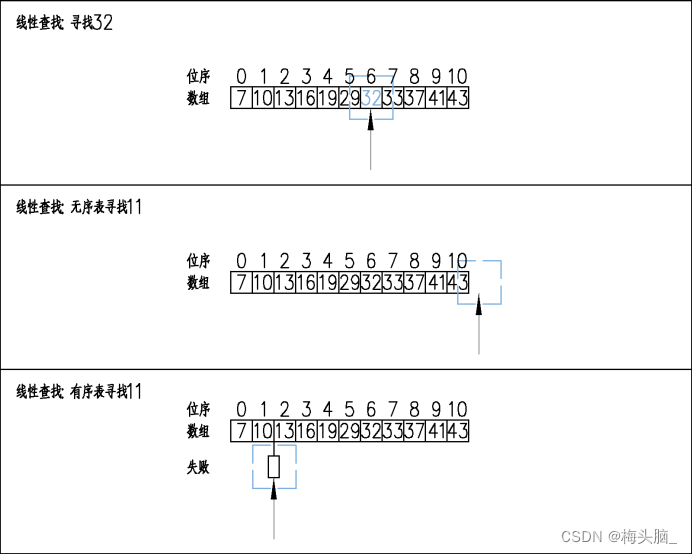
接下来我们分析二者查找次数的区别：例如这个11位数组，第0位要查1次，第1位要查2次，以此类推，越靠后的数字需要查询的次数也就越多~

无序查找的失败仅有1种情况，就是查找了队列的末尾；
有序查找的失败有n+1种情况，例如位序0前失败要查1次，位序1前失败要查2次...位序10前、后都有可能失败，即位序10要查11x2=22次~

无序|有序查找成功平均次数： $ASL_{succ}=\frac{1+2+...+n}{n}=\frac{n+1}{2}$
无序查找成功失败次数： $ASL_{fail}=n+1$
有序查找成功失败次数： $ASL_{fail}=\frac{1+2+...+n+n}{n+1}=\frac{n}{2}+\frac{n}{n+1}$

以下是有序查找和无序查找的代码，差别只有结束查找的判定的那一行~

#include <iostream>
#include <vector>
using namespace std;

// 顺序查找函数
int sequentialSearch(const vector<int>& vec, int target) {
    //for (int i = 0; i < vec.size(); i++) {   //  适用：普通数组
    for (int i = 0; i < vec.size() && vec[i] <= target; i++){    //  适用：有序数组
        if (vec[i] == target) {
            return i; // 返回目标元素在数组中的索引
        }
    }
    return -1; // 目标元素不存在，返回-1
}

// 输出查找结果的函数
void printSearchResult(int index, int target) {
    if (index != -1) {
        cout << "目标元素 " << target << " 在数组中的索引为：" << index << endl;
    } else {
        cout << "目标元素 " << target << " 不存在于数组中！" << endl;
    }
}

int main() {
    vector<int> vec = {7, 10, 13, 16, 19, 29, 32, 33, 37, 41, 43};

    int target1 = 32; // 要查找的目标元素
    int result1 = sequentialSearch(vec, target1);
    printSearchResult(result1, target1);

    int target2 = 11; // 要查找的目标元素
    int result2 = sequentialSearch(vec, target2);
    printSearchResult(result2, target2);

    return 0;
}

查询结果如下：

⌨️折半查找

线性查找又称二分查找，仅适合于有序的顺序表。查找的结果如下：

有两个指针框定查找的范围，左指针初始指向数组开头，右指针初始指向数组结尾；mid锁定需要查找的元素位置，是 [左指针+右指针]/2，结果向上取整；
判定查找：
元素mid = 被查找元素key，查找成功，完结撒花~
元素mid < 被查找元素key，查找失败；经过本轮的比较，已知mid≠key，那么就将右指针(right或high)指向mid-1,左指针(left或low)不变，mid依然是[左指针+右指针]/2，结果向下取整；
元素mid > 被查找元素key，查找失败；经过本轮的比较，已知mid≠key，那么就将右指针(right或high)指向mid+1,左指针(left或low)不变，mid依然是[左指针+右指针]/2，结果向下取整；

有关查找次数，举个王道书的栗子，我们寻找数字11：

第1轮 11<29	7	10	13	16	19	29	32	33	37	41	43
第1轮 11<29	左					中					右
第2轮 11<13	7	10	13	16	19	29	32	33	37	41	43
第2轮 11<13	左		中		右
第3轮 11>7	7	10	13	16	19	29	32	33	37	41	43
第3轮 11>7	左中	右
第4轮 11≠10	7	10	13	16	19	29	32	33	37	41	43
第4轮 11≠10		左中右

如何计算平均查找长度？首先我们要确定，成功结点与失败结点各需要查找的次数，在本栗中：

查29在第1轮就能被mid指针查到；
查13、37需要在第2轮才能被mid指针查到；
查7、16、32、41需要在第3轮才能被mid指针查到；
查10、19、33、43需要在第4轮才能被mid指针查到；
以上是成功的情况，还有失败的情况要考虑，例如<7是第3轮被查到，7~10是第4轮被查到；

这么傻傻地推算1个数组，费劲耗时且按下不表，关键越繁琐的步骤越容易出错，例如脑子迷糊，忘记下一轮需要mid-1，把数字10归到了第3轮怎么办呀？于是我们就可以通过二叉树画出各个结点成功与失败的查找次数，便于检查，如图——

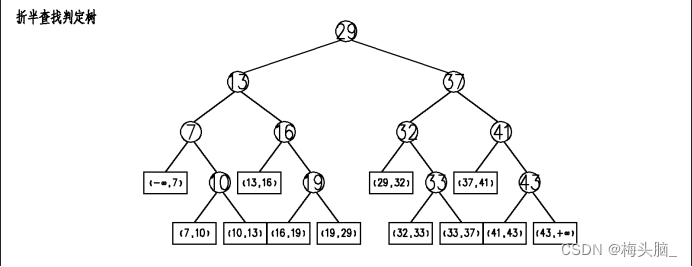
ASL成功：[Σ(层数x本层成功结点数)]/所有成功结点数=[1x1+2x2+3x4+4x4]/11=3次
ASL失败：[Σ((层数-1)x本层失败结点数)]/所有失败结点数=[3x4+4x8]/12=11/3次

失败结点层数要-1，因为在最后一轮比较时缩小为1个数字，可以确定查询是否成功或者失败~

根据二叉树高度的计算公式，这棵树在最理想的情况查找的时间复杂度是O(logn)；
忘记树高计算公式了？大胶布，可以看向这里🌸数据结构05：树与二叉树[C++]

代码如下：

#include <iostream>
#include <vector>
using namespace std;

// 折半查找函数
int binarySearch(const vector<int>& arr, int target) {
    int left = 0; // 左边界
    int right = arr.size() - 1; // 右边界

    while (left <= right) {
        int mid = left + (right - left) / 2; // 计算中间位置

        if (arr[mid] == target) {
            return mid; // 找到目标元素，返回索引
        } else if (arr[mid] < target) {
            left = mid + 1; // 目标在右半部分，更新左边界
        } else {
            right = mid - 1; // 目标在左半部分，更新右边界
        }
    }

    return -1; // 目标元素不存在，返回-1
}

// 输出查找结果的函数
void printSearchResult(int index, int target) {
    if (index != -1) {
        cout << "目标元素 " << target << " 在数组中的索引为：" << index << endl;
    } else {
        cout << "目标元素 " << target << " 不存在于数组中！" << endl;
    }
}

int main() {
    vector<int> arr = {7, 10, 13, 16, 19, 29, 32, 33, 37, 41, 43};

    int target1 = 32; // 要查找的目标元素
    int result1 = binarySearch(arr, target1);
    printSearchResult(result1, target1);

    int target2 = 11; // 要查找的目标元素
    int result2 = binarySearch(arr, target2);
    printSearchResult(result2, target2);

    return 0;
}

查询结果如下：

⌨️分块查找

适合顺序表、链表，索引表内通常取每个块的最大值，且索引表可能是需要单独占用空间的~

呃，关于这个我要备注一下：

块内的位序可以是无序的，因此在块内可以采用顺序查找；例如比较11时：
1. 第三轮块内查找：数组10、12、14、16，从开始遍历到末尾，4个元素失败查询共需遍历5次，执行到末尾后返回失败~
2. 第二轮索引表：11<16，可以锁定我们的元素在第二块(6,16]的位置；
3. 第一轮索引表：11>6，向后查询；
块间[也就是索引表]的位序必须是有序的，因此在块间既可以采用顺序查找，也可以采用折半查找，此处仅列成功的查找次数：
1. 块间顺序查找、块内顺序查找：(b+1)/2+(s+1)/2；
2. 块间折半查找、块内顺序查找：log(b+1)+(s+1)/2；

这是一个简化版代码，虽然能跑，但是怎么看也有点不像是很实用的样子，感兴趣的小伙伴也可以浏览一下~

#include <iostream>
#include <vector>
using namespace std;

// 块内顺序查找函数
int blockSequentialSearch(const vector<int>& block, int target) {
    for (int i = 0; i < block.size(); i++) {
        if (block[i] == target) {
            return i; // 返回目标元素在块内的索引
        }
    }
    return -1; // 目标元素不存在，返回-1
}

// 分块查找函数
int blockSearch(const vector<vector<int>>& blocks, const vector<int>& index, int target) {
    // 在索引表中查找目标所在的块
    int blockIndex = -1;
    for (int i = 0; i < index.size(); i++) {
        if (target <= index[i]) {
            blockIndex = i;
            break;
        }
    }

    // 在对应块内使用块内顺序查找
    if (blockIndex != -1) {
        return blockSequentialSearch(blocks[blockIndex], target);
    }

    return -1; // 目标元素不存在，返回-1
}

// 输出查找结果的函数
void printSearchResult(int index, int target) {
    if (index != -1) {
        cout << "目标元素 " << target << " 在数组中的索引为：" << index << endl;
    } else {
        cout << "目标元素 " << target << " 不存在于数组中！" << endl;
    }
}

int main() {
    vector<vector<int>> blocks = {{2, 4, 6}, {10, 12, 14, 16}, {20, 22, 24}, {30, 32, 34, 36, 38}};
    vector<int> index = {6, 16, 24, 38}; // 索引表，记录每个块的块内最大值

    int target1 = 12; // 要查找的目标元素
    int result1 = blockSearch(blocks, index, target1);
    printSearchResult(result1, target1);

    int target2 = 25; // 要查找的目标元素
    int result2 = blockSearch(blocks, index, target2);
    printSearchResult(result2, target2);

    return 0;
}

查询结果如下：