机器学习(课后作业–hw1)
本篇文章全文参考这篇blog
网上找了很多教程,这个是相对来说清楚的,代码可能是一模一样,只是进行了一些微调,但是一定要理解这个模型具体的处理方法,这个模型我认为最巧妙的它对于数据的处理,直接把前9天所有的参数参数当作变量,最简单粗暴的方法,,然后再是里面一些矩阵的运算,也很重要,可能直接看无法理解,那就手动创造几个数据,进行手动模拟,一定会有不小的收获的
作业介绍
题目要求:利用每天的前9个小时的18个特征(包括PM2.5),来预测第10个小时的PM2.5的值。
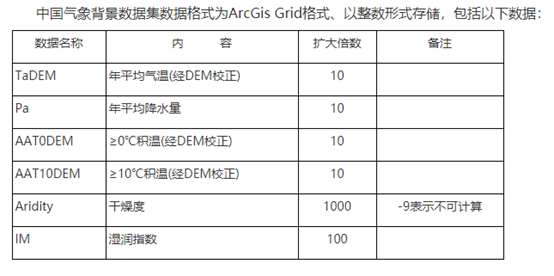
特征包括: AMB_TEMP, CH4, CO, NHMC, NO, NO2, NOx, O3, PM10, PM2.5, RAINFALL, RH, SO2, THC, WD_HR, WIND_DIREC, WIND_SPEED, WS_HR,总计18种。每一种都可以作为一个变量加入你的模型里面。
数据下载:Github链接
下载结束以后把文件放入对应的文件夹里面就好了
CSV文件,包含台湾丰原地区240天的气象观测资料(取每个月前20天的数据做训练集,12月X20天=240天,每月后10天数据用于测试,对学生不可见)
作业任务:根据每月的观测数据对未来进行预测
题目分析
Dataset里面我们要用的两个csv文件:数据集(train.csv)和测试集(test.csv)。
数据集中记录了12个月的前20天每天24个小时的18个物质浓度的资料,然后测试集就是剩余的数据中再取的。从上述我们可以得到以下结论:
- 模型的输入:前9个小时的观测数据,每小时18个数据,所以输入参数有9*18个参数值
- 模型的输出:预测第十个小时的PM2.5浓度
- 模型:回归模型(Regression Model)
- 要求:根据前面连续9个小时的观测数据,预测接下来一个小的PM2.5浓度
- 每一天的信息:(18,24)(18个指标,24个小时)
- 训练数据:
训练数据是连续9个小时的观测数据,接下来一个小时的PM2.5作为这个训练数据集的label
注意:每小时的数据可以作为训练数据,也可以作为label,一共12个月,每个月20天,一天24小时,每天18个观测数据,所以一共有(2024)x18个数据,而训练数据集有2024-9=471个(因为最开始的9个无法作为数据集的label)
代码解答
1. Data Preprocessing
我们需要做的第一件事就是数据的读入和预处理:
- 按照文件路径读入
- 去除无用数据
- 预处理
- 数据转化
# 引入必要的包
import pandas as pd
import numpy as np
# 读取数据保存到data中,路径根据你保存的train.csv位置而有变化
# 数据编码方式,这里选择big5,台湾是繁体字,使用utf-8可能会出现问题
data = pd.read_csv('Dataset/train.csv', encoding='big5')
# print(data)
# 行保留所有,列从第三列开始往后才保留,这样去除了数据中的时间、地点、参数等信息
data = data.iloc[:, 3:]
# print(data)
# 将所有NR的值全部置为0方便之后处理
data[data == 'NR'] = 0
# print(data)
# 将data的所有数据转换为二维数据并用raw_data来保存
raw_data = data.to_numpy()
# print(raw_data)
# 可以每一步都打印出结果,看到数据的变化
2. Feature Engineering
按照train.csv给出的数据,肯定是无法满足我们的使用,我们在进行提取数据集的时候,把一个月的数据全部放在一起,只取连续的9个小时,不管是那一天的,使用我们原先的
按天数竖着排列修改为每个月的数据按天数横着排放,这个代码进行实现其实不困,就是不好理解。
处理以后才更方便我们提取连续的9小时数据作为数据集和接下来1小时PM2.5作为对于数据集的label
month_data = {}
# month 从0-11 共12个月
# 返回一个18行480列的数组,保存一个月的data(一月20天,一天24小时)
# day从0-19 共20天
for month in range(12):
sample = np.empty([18, 480])
for day in range(20):
# raw的行每次取18行,列取全部列。送到sample中(sample是18行480列)
# 行给全部行,列只给24列,然后列往后增加
sample[:, day * 24: (day + 1) * 24] = raw_data[18 * (20 * month + day): 18 * (20 * month + day + 1), :]
month_data[month] = sample
- 创建字典,month为key,sample为value
- 循环遍历:sample和raw_data都是两个参数(行和列),行和列都在变化,但是我们都是优先是行,然后是列(这个建议自己手动演示一下,这个代码真的很奇妙)
- month = 0,day = 0
遍历raw_data的第0行(0到18-1)的每一列(一共24列),依次赋值给sample的第0行(一共18行)的第0到24-1列。- month = 0,day = 1
遍历raw_data的第18行(18到182-1)的每一列(一共24列),依次赋值给sample的第0行(一共18行)的第24到242-1列。
真的发现自己和zz一样,python最大的优点就是神奇,python可以直接实现矩阵对应块赋值,所以我们之间进行整块转移就好了,那就很好理解了,
raw_data其实每遍历一次就是去除一天的数据量,sample其实也就是取出前一天后面那一块。
经过上面的处理,数据已经横向转化为方便我们提取训练集的数据集了

# 每月共480个小时,每9个小时一个数据(480列最后一列不可以计入,如果取到最后一列那么最后一个数据
# 便没有了结果{需要9个小时的输入和第10个小时的第10行作为结果}),480-1-9+1=471。
# 12个月共12*471个数据按行排列,每一行一个数据;数据每小时有18个特征,而每个数据9个小时,共18*9列
x = np.empty([12 * 471, 18 * 9], dtype=float)
# 12个月共12*471个数据,每个数据对应一个结果,即第10小时的PM2.5浓度,也就是提取对应label
y = np.empty([12 * 471, 1], dtype=float)
for month in range(12): # month 0-11
for day in range(20): # day 0-19
for hour in range(24): # hour 0-23
if day == 19 and hour > 14: # 第20天的第23时
continue
# 取对应month:行都要取,列取9个,依次进行,最后将整个数据reshape成一行数据
# (列数无所谓)。然后赋给x,x内的坐标只是为了保证其从0-471*12
# vector dim:18*9
x[month * 471 + day * 24 + hour, :] = month_data[month][:, day * 24 + hour: day * 24 + hour + 9].reshape(1, -1)
# value,结果对应的行数一直是9行(即第10行PM2.5)然后列数随着取得数据依次往后进行
y[month * 471 + day * 24 + hour, 0] = month_data[month][9, day * 24 + hour + 9]
3. Data Normalization
数据的标准化我在另外一篇博客里面提到过
数据的标准化(normalization)是将数据按比例缩放,使之落入一个小的特定区间。去除数据的单位限制,将其转化为无量纲的纯数值,便于不同单位或量级的指标能够进行比较和加权。
这里我们采用的是最简单的标准化公式:
x* = (x - μ ) / σ
其中μ为所有样本数据的均值,σ为所有样本数据的标准差。
标准化其实是为了让模型更快收敛
mean_x = np.mean(x, axis=0) # 18 * 9 求均值,axis = 0表示对各列求值,返回 1* 列数 的矩阵
std_x = np.std(x, axis=0) # 18 * 9 求标准差,axis = 0表示对各列求值,返回 1* 列数 的矩阵
for i in range(len(x)): # 12 * 471
for j in range(len(x[0])): # 18 * 9
if std_x[j] != 0:
x[i][j] = (x[i][j] - mean_x[j]) / std_x[j]
4. Splitting Data
将训练数据按8:2拆成训练数据和验证数据。训练数据用于模型的训练,测试数据用于模型的检测,这样可以让我们了解自己建立的模型面对新的数据集的时候的表现。
x_train_set = x[: math.floor(len(x) * 0.8), :]
y_train_set = y[: math.floor(len(y) * 0.8), :]
x_validation = x[math.floor(len(x) * 0.8):, :]
y_validation = y[math.floor(len(y) * 0.8):, :]
5. Model Training:
5.1 Regression Model
采用最普通的线性回归模型,如下列公式所展示,我们在前面将每一组训练数据集进训练压缩,成为一行,所以这一行一共有9*18个变量,每个变量都有其对应的权重(参数),同时还设置了一个偏置(bias)
y = ∑ i = 0 9 ∗ 18 ω i ⋅ x i + b y = \sum_{i=0}^{9*18}{{\omega}_i} \cdot{x_i} + b y=i=0∑9∗18ωi⋅xi+b
xi为对应训练数据集中第i个变量,wi为其对应的权重值,b为偏置项,y为该数据帧样本的预测结果。
5.2 模型训练
数据在进行了前置的处理以后,,我们就要开始训练自己的模型了,我们这里使用的是损失函数Loss和Adagrad算法对参数进行优化。
均方根误差(Root Mean Square Error)
R M S E = 1 n ∑ i = 1 n ( y i − y ^ i ) 2 RMSE = \sqrt{\frac{1}{n}\sum_{i=1}^{n}(y_i - \hat{y}_i)^2} RMSE=n1i=1∑n(yi−y^i)2
Adagrad算法
ω t + 1 = ω t − η ∑ i = 0 t ( g i ) 2 + ϵ g t \omega^{t+1} = \omega^t - \frac{\eta}{\sqrt{\sum_{i=0}^t(g^i)^2 + \epsilon}}g^t ωt+1=ωt−∑i=0t(gi)2+ϵηgt
其中 η \eta η是学习率, g i g^i gi是第i次训练得到的梯度, ϵ \epsilon ϵ是一个极小正值,防止分母为0
这部分建议先对着代码看一遍,然后按照我写的过程理解一下,矩阵部分求导有点复杂,有兴趣的可以了解一下
# 用来做参数vector的维数,加1是为了对bias好处理(还有个误差项)。即h(x)=w1x1+w2x2+''+wnxn+b
dim = 18 * 9 + 1
# 生成一个dim行1列的数组用来保存参数值
w = np.ones([dim, 1])
# np.ones来生成12*471行1列的全1数组,np.concatenate,axis=1
# 表示按列将两个数组拼接起来,即在x最前面新加一列内容,之前x是12*471行
# 18*9列的数组,新加一列之后变为12*471行18*9+1列的数组'''
x = np.concatenate((np.ones([12 * 471, 1]), x), axis=1).astype(float)
learning_rate = 100 # 学习率
iter_time = 10000 # 迭代次数
# 生成dim行即163行1列的数组,用来使用adagrad算法更新学习率
adagrad = np.zeros([dim, 1])
# 因为新的学习率是learning_rate/sqrt(sum_of_pre_grads**2),
# 而adagrad=sum_of_grads**2,所以处在分母上而迭代时adagrad可能为0,
# 所以加上一个极小数,使其不除0
eps = 0.0000000001
for t in range(iter_time):
# rmse loss函数是从0-n的(X*W-Y)**2之和/(471*12)再开根号,
# 即使用均方根误差(root mean square error),具体可看公式,
# /471/12即/N(次数)'''
loss = np.sqrt(np.sum(np.power(np.dot(x, w) - y, 2)) / 471 / 12)
if (t % 100 == 0): # 每一百次迭代就输出其损失
print(str(t) + ":" + str(loss))
# dim*1 x.transpose即x的转置,后面是X*W-Y,即2*(x的转置*(X*W-Y))是梯度,
# 具体可由h(x)求偏微分获得.最后生成1行18*9+1列的数组。转置后的X,其每一行
# 是一个参数,与h(x)-y的值相乘之后是参数W0的修正值,同理可得W0-Wn的修正值
# 保存到1行18*9+1列的数组中,即gradient
# 计算梯度。梯度是损失函数对参数向量w的偏导数
gradient = 2 * np.dot(x.transpose(), np.dot(x, w) - y)
# adagrad用于保存前面使用到的所有gradient的平方,进而在更新时用于调整学习率
adagrad += gradient ** 2
w = w - learning_rate * gradient / np.sqrt(adagrad + eps) # 更新权重
np.save('weight.npy', w) # 将参数保存下来

6. Model Evaluation
在前面进行数据集划分的时候,我们将数据集划分为了两部分,按照8:2的比例,分别进行训练和测试。
但是我这里采用的是全部数据进行训练,然后使用我们分出来的那部分数据进行测试,这样效果相较于其他处理方式,效果较好。
一般来说,数据集的划分比较随意,我们也习惯多次划分尝试,然后对模型得到的参数进行评估,然后选择最好的数据集划分方式。
w = np.load('weight.npy')
# 使用x_validation和y_validation来计算模型的准确率,因为X已经normalize了,
# 所以不需要再来一遍,只需在x_validation上添加新的一列作为bias的乘数即可
x_validation = np.concatenate((np.ones([1131, 1]), x_validation), axis=1).astype(float)
ans_y = np.dot(x_validation, w)
loss = np.sqrt(np.sum(np.power(ans_y - y_validation, 2)) / 1131)
print(loss)
7. Test Data Prediction
7.1 测试数据预处理
测试数据的预处理和前面的训练数据预处理很类似,直接按部就班就好了
testdata = pd.read_csv('Dataset/test.csv', header=None, encoding='big5')
test_data = testdata.iloc[:, 2:] # 取csv文件中的全行数即第3列到结束的列数所包含的数据
test_data.replace('NR', 0, inplace=True) # 将testdata中的NR替换为0
test_data = test_data.to_numpy() # 将其转换为数组
# 创建一个240行18*9列的空数列用于保存textdata的输入
test_x = np.empty([240, 18 * 9], dtype=float)
for i in range(240): # 共240个测试输入数据
test_x[i, :] = test_data[18 * i: 18 * (i + 1), :].reshape(1, -1)
# 下面是Normalize,且必须跟training data是同一种方法进行Normalize
for i in range(len(test_x)):
for j in range(len(test_x[0])):
if std_x[j] != 0:
test_x[i][j] = (test_x[i][j] - mean_x[j]) / std_x[j]
# 在test_x前面拼接一列全1数组,构成240行,163列数据
test_x = np.concatenate((np.ones([240, 1]), test_x), axis=1).astype(float)
7.2 数据预测
单纯的矩阵相乘,原理很简单,得到一个列向量,分别对应每一组数据集未来一小时的PM2.5预测值
# 进行预测
w = np.load('weight.npy')
ans_y = np.dot(test_x, w) # test data的预测值ans_y=test_x与W的积
8. Saving Predictions
最后一步当然是把数据存入文件里
# 将预测结果填入文件当中
import csv
with open('submit.csv', mode='w', newline='') as submit_file:
csv_writer = csv.writer(submit_file)
header = ['id', 'value']
print(header)
csv_writer.writerow(header)
for i in range(240):
row = ['id_' + str(i), ans_y[i][0]]
csv_writer.writerow(row)
print(row)
完整代码
这是我文件的一些对应存放位置,调整好了应该就可以直接运行
# 引入必要的包
import pandas as pd
import numpy as np
# 读取数据保存到data中,路径根据你保存的train.csv位置而有变化
# 数据编码方式,这里选择big5,台湾是繁体字,使用utf-8可能会出现问题
data = pd.read_csv('Dataset/train.csv', encoding='big5')
# print(data)
# 行保留所有,列从第三列开始往后才保留,这样去除了数据中的时间、地点、参数等信息
data = data.iloc[:, 3:]
# print(data)
# 将所有NR的值全部置为0方便之后处理
data[data == 'NR'] = 0
# print(data)
# 将data的所有数据转换为二维数据并用raw_data来保存
raw_data = data.to_numpy()
# print(raw_data)
# 可以每一步都打印出结果,看到数据的变化
month_data = {}
# month 从0-11 共12个月
# 返回一个18行480列的数组,保存一个月的data(一月20天,一天24小时)
# day从0-19 共20天
for month in range(12):
sample = np.empty([18, 480])
for day in range(20):
# raw的行每次取18行,列取全部列。送到sample中(sample是18行480列)
# 行给全部行,列只给24列,然后列往后增加
sample[:, day * 24: (day + 1) * 24] = raw_data[18 * (20 * month + day): 18 * (20 * month + day + 1), :]
month_data[month] = sample
# 每月共480个小时,每9个小时一个数据(480列最后一列不可以计入,如果取到最后一列那么最后一个数据
# 便没有了结果{需要9个小时的输入和第10个小时的第10行作为结果}),480-1-9+1=471。
# 12个月共12*471个数据按行排列,每一行一个数据;数据每小时有18个特征,而每个数据9个小时,共18*9列
x = np.empty([12 * 471, 18 * 9], dtype=float)
# 12个月共12*471个数据,每个数据对应一个结果,即第10小时的PM2.5浓度,也就是提取对应label
y = np.empty([12 * 471, 1], dtype=float)
for month in range(12): # month 0-11
for day in range(20): # day 0-19
for hour in range(24): # hour 0-23
if day == 19 and hour > 14: # 第20天的第23时
continue
# 取对应month:行都要取,列取9个,依次进行,最后将整个数据reshape成一行数据
# (列数无所谓)。然后赋给x,x内的坐标只是为了保证其从0-471*12
# vector dim:18*9
x[month * 471 + day * 24 + hour, :] = month_data[month][:, day * 24 + hour: day * 24 + hour + 9].reshape(1, -1)
# value,结果对应的行数一直是9行(即第10行PM2.5)然后列数随着取得数据依次往后进行
y[month * 471 + day * 24 + hour, 0] = month_data[month][9, day * 24 + hour + 9]
mean_x = np.mean(x, axis=0) # 18 * 9 求均值,axis = 0表示对各列求值,返回 1* 列数 的矩阵
std_x = np.std(x, axis=0) # 18 * 9 求标准差,axis = 0表示对各列求值,返回 1* 列数 的矩阵
for i in range(len(x)): # 12 * 471
for j in range(len(x[0])): # 18 * 9
if std_x[j] != 0:
x[i][j] = (x[i][j] - mean_x[j]) / std_x[j]
# 将训练数据拆成训练数据:验证数据=8:2,这样用来验证
import math
x_train_set = x[: math.floor(len(x) * 0.8), :]
y_train_set = y[: math.floor(len(y) * 0.8), :]
x_validation = x[math.floor(len(x) * 0.8):, :]
y_validation = y[math.floor(len(y) * 0.8):, :]
# 用来做参数vector的维数,加1是为了对bias好处理(还有个误差项)。即h(x)=w1x1+w2x2+''+wnxn+b
dim = 18 * 9 + 1
# 生成一个dim行1列的数组用来保存参数值
w = np.ones([dim, 1])
# np.ones来生成12*471行1列的全1数组,np.concatenate,axis=1
# 表示按列将两个数组拼接起来,即在x最前面新加一列内容,之前x是12*471行
# 18*9列的数组,新加一列之后变为12*471行18*9+1列的数组'''
x = np.concatenate((np.ones([12 * 471, 1]), x), axis=1).astype(float)
learning_rate = 100 # 学习率
iter_time = 10000 # 迭代次数
# 生成dim行即163行1列的数组,用来使用adagrad算法更新学习率
adagrad = np.zeros([dim, 1])
# 因为新的学习率是learning_rate/sqrt(sum_of_pre_grads**2),
# 而adagrad=sum_of_grads**2,所以处在分母上而迭代时adagrad可能为0,
# 所以加上一个极小数,使其不除0
eps = 0.0000000001
for t in range(iter_time):
# rmse loss函数是从0-n的(X*W-Y)**2之和/(471*12)再开根号,
# 即使用均方根误差(root mean square error),具体可看公式,
# /471/12即/N(次数)'''
loss = np.sqrt(np.sum(np.power(np.dot(x, w) - y, 2)) / 471 / 12)
if (t % 100 == 0): # 每一百次迭代就输出其损失
print(str(t) + ":" + str(loss))
# dim*1 x.transpose即x的转置,后面是X*W-Y,即2*(x的转置*(X*W-Y))是梯度,
# 具体可由h(x)求偏微分获得.最后生成1行18*9+1列的数组。转置后的X,其每一行
# 是一个参数,与h(x)-y的值相乘之后是参数W0的修正值,同理可得W0-Wn的修正值
# 保存到1行18*9+1列的数组中,即gradient
# 计算梯度。梯度是损失函数对参数向量w的偏导数
gradient = 2 * np.dot(x.transpose(), np.dot(x, w) - y)
# adagrad用于保存前面使用到的所有gradient的平方,进而在更新时用于调整学习率
adagrad += gradient ** 2
w = w - learning_rate * gradient / np.sqrt(adagrad + eps) # 更新权重
np.save('weight.npy', w) # 将参数保存下来
w = np.load('weight.npy')
# 使用x_validation和y_validation来计算模型的准确率,因为X已经normalize了,
# 所以不需要再来一遍,只需在x_validation上添加新的一列作为bias的乘数即可
x_validation = np.concatenate((np.ones([1131, 1]), x_validation), axis=1).astype(float)
ans_y = np.dot(x_validation, w)
loss = np.sqrt(np.sum(np.power(ans_y - y_validation, 2)) / 1131)
print(loss)
testdata = pd.read_csv('Dataset/test.csv', header=None, encoding='big5')
test_data = testdata.iloc[:, 2:] # 取csv文件中的全行数即第3列到结束的列数所包含的数据
test_data.replace('NR', 0, inplace=True) # 将testdata中的NR替换为0
test_data = test_data.to_numpy() # 将其转换为数组
# 创建一个240行18*9列的空数列用于保存textdata的输入
test_x = np.empty([240, 18 * 9], dtype=float)
for i in range(240): # 共240个测试输入数据
test_x[i, :] = test_data[18 * i: 18 * (i + 1), :].reshape(1, -1)
# 下面是Normalize,且必须跟training data是同一种方法进行Normalize
for i in range(len(test_x)):
for j in range(len(test_x[0])):
if std_x[j] != 0:
test_x[i][j] = (test_x[i][j] - mean_x[j]) / std_x[j]
# 在test_x前面拼接一列全1数组,构成240行,163列数据
test_x = np.concatenate((np.ones([240, 1]), test_x), axis=1).astype(float)
# 进行预测
w = np.load('weight.npy')
ans_y = np.dot(test_x, w) # test data的预测值ans_y=test_x与W的积
# 将预测结果填入文件当中
import csv
with open('submit.csv', mode='w', newline='') as submit_file:
csv_writer = csv.writer(submit_file)
header = ['id', 'value']
print(header)
csv_writer.writerow(header)
for i in range(240):
row = ['id_' + str(i), ans_y[i][0]]
csv_writer.writerow(row)
print(row)