一、本周周赛总结

• 双周赛就是难，没打就对了。
• T1模拟。
• T2暴力。
• T3脑筋急转弯。
• T4贪心。

二、 [Easy] 6261. 数组中字符串的最大值

链接: 6261. 数组中字符串的最大值

1. 题目描述

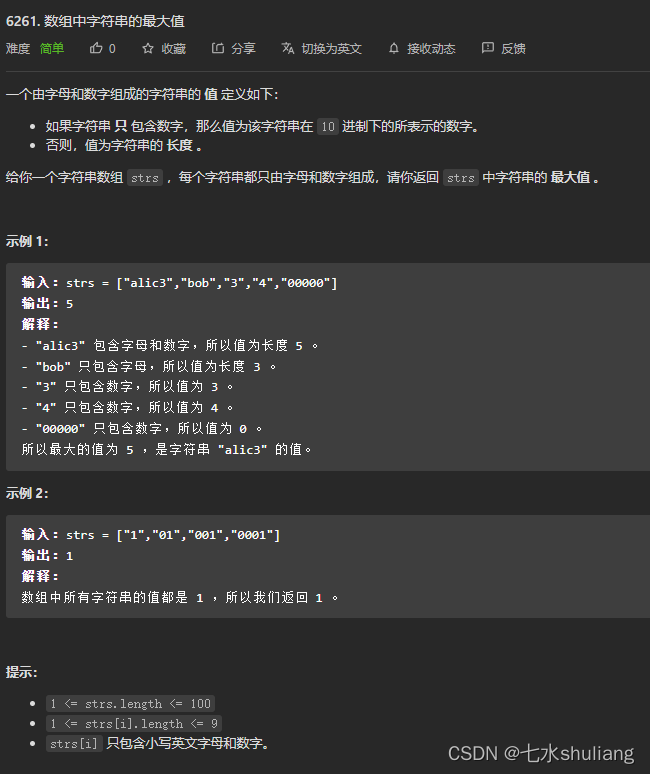
2. 思路分析

按题意模拟即可。

3. 代码实现

class Solution:
    def maximumValue(self, strs: List[str]) -> int:
        return max(int(s) if s.isdigit()  else len(s) for s in strs)

三、[Medium] 6262. 图中最大星和

链接: 6262. 图中最大星和

1. 题目描述

2. 思路分析

遍历每个节点作为中心。

• 注意负数的邻居不需要。

3. 代码实现

class Solution:
    def maxStarSum(self, vals: List[int], edges: List[List[int]], k: int) -> int:
        n = len(vals)
        g = [[] for _ in range(n)]
        for u,v in edges:
            if vals[v] >0:
                g[u].append(vals[v])
            if vals[u] > 0:
                g[v].append(vals[u])        
       
        return max(u +sum(nlargest(k,v)) for u,v in zip(vals,g) )

四、[Medium] 6263. 青蛙过河 II

链接: 6263. 青蛙过河 II

1. 题目描述

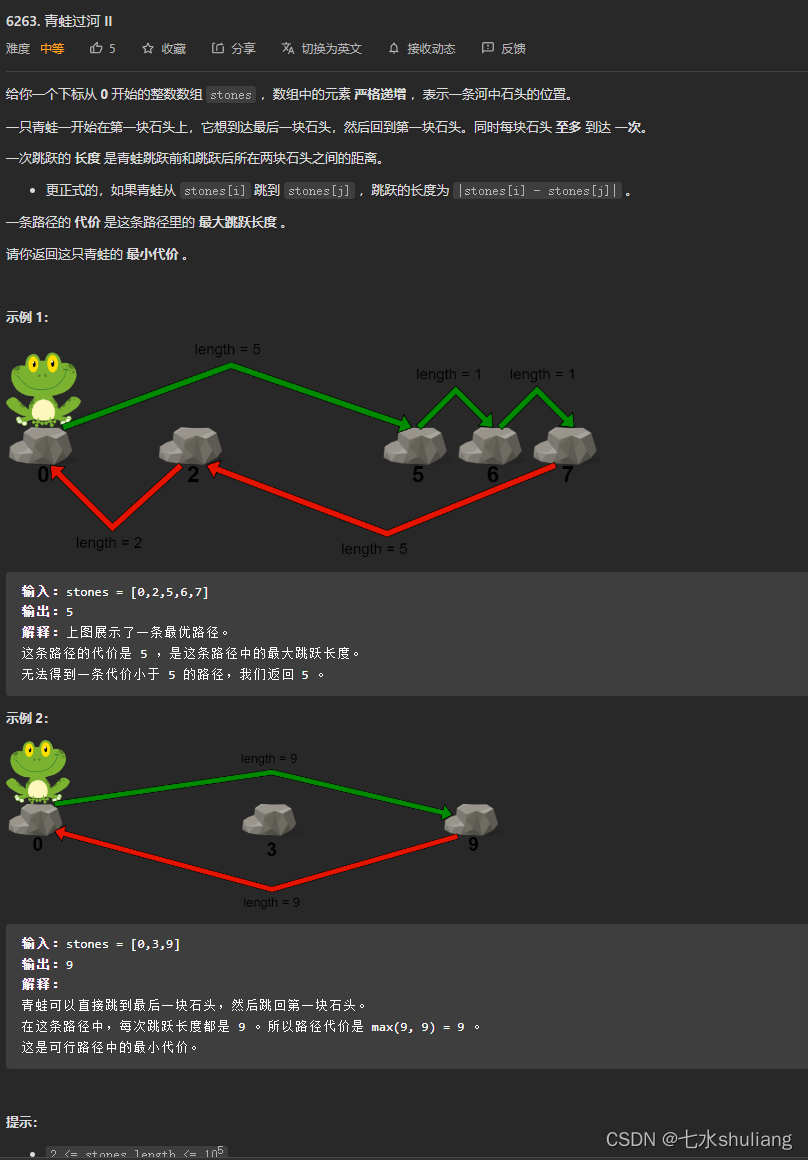
2. 思路分析

• 由于每个石头只能用一次，因此最少要间隔跳，模拟一下发现间隔跳一定是最优的，因为否则的话一定存在一个包含关系，超过间隔跳。

---

• 另外由于本题是最大值最小化，因此可以二分；
• 定义函数为在limit作为答案下，能否过河，每步选择最远那个最优。

3. 代码实现

class Solution:
    def maxJump(self, stones: List[int]) -> int:
        n = len(stones)

        ans = stones[1] - stones[0]
        for i in range(2,n):
            ans = max(ans,stones[i]-stones[i-2])
        return ans

五、[Hard] 6264. 让数组不相等的最小总代价

链接: 6264. 让数组不相等的最小总代价

1. 题目描述

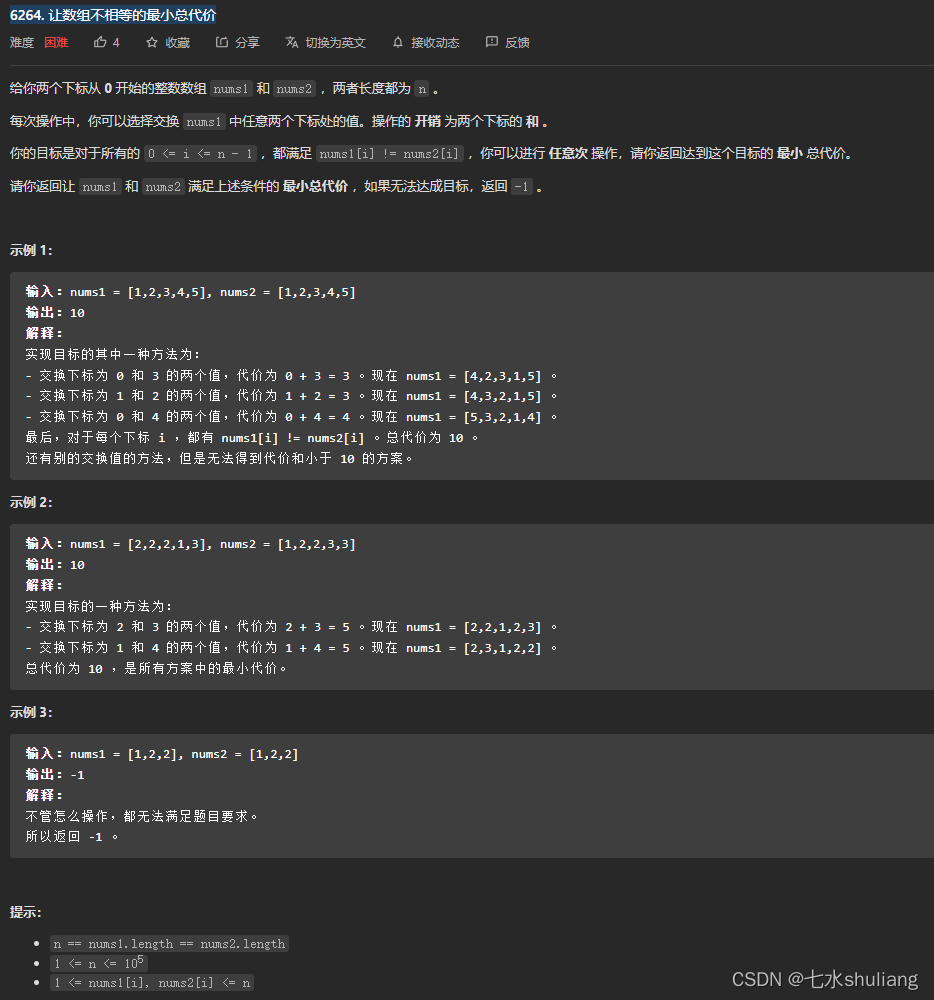
2. 思路分析

• 贪心。

---

• 先把下标分为两组swap组和keep组：需要交换位置（即num1[i]==num2[i]）和不需要交换的位置（即nums1[i]!=nums2[i]）。
• 计数需要交换的位置，有swap个，显然这些数无论如何至少参与答案一次，ans+=sum(i)。
• 我们希望代价最小，那么最好keep组别动，swap组内部交换即可；如果满足，那么可以return ans
• 什么时候满足呢，即swap组中的众数不超过组的一半：
  • 这时，如果swap是偶数，两两交换即可；
  • 如果是奇数，让nums[0]参与swap组，贡献不变。
• 如果不满足，需要让keep组中的数加入swap组，由于我们希望贡献尽可能小，因此从低位开始加入。直到满足。

3. 代码实现

class Solution:
    def minimumTotalCost(self, nums1: List[int], nums2: List[int]) -> int:
        n = len(nums1)
        # c1,c2 = Counter(nums1),Counter(nums2)
        cnt = Counter(nums1+nums2)
        if max(cnt.values())>n:
            return -1
        
        cnt = Counter()
        mode = 0
        same = 0
        ans = 0
        mode_cnt = 0
        for i,a,b in zip(range(n),nums1,nums2):
            if a == b:
                same += 1
                cnt[a] += 1
                ans += i
                if cnt[a]>cnt[mode]:
                    mode = a 
        mode_cnt = cnt[mode]
        # print(mode,cnt,mode_cnt,ans,same)
        for i,a,b in zip(range(n),nums1,nums2):
            if mode_cnt*2 <= same:
                return ans 
            if a!=mode!=b!=a:
                ans += i 
                same += 1
        return ans

六、参考链接