1. 基本思路

重投影误差表示为e, 相机的位姿表示为ξ (或者表示为T=(R,t))， 空间点表示为P, 则空间点投影到相机坐标系下的空间坐标点的相机坐标表示为P'=[X', Y', Z'], 则

重投影误差e对于相机的位姿ξ的雅克比矩阵表示为

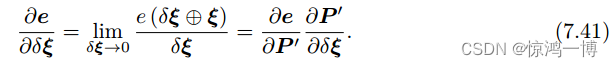
分别求等式右侧的两半部分（误差对空间点的相机坐标的导数，和 空间点的相机坐标对相机位姿的导数），然后相乘即可。

同理， 重投影误差e对于空间点的坐标P的雅可比矩阵，可以表示为

 分别求等式右侧的两半部分（误差对空间点的相机坐标的导数，和 空间点的相机坐标对空间点视觉坐标的导数），然后相乘即可。

最终结果，见下面的公式(7.45) 和 (7.47)

2. 具体推导过程

参考视觉slam十四讲，第7章

残差(重投影误差)对相机位姿的导数（雅克比矩阵）:

残差(重投影误差)对landmark的导数（雅克比矩阵）:

        于是，我们推导了观测相机方程关于相机位姿与特征点的两个导数矩阵。它们十分重要，能够在优化过程中提供重要的梯度方向，指导优化的迭代。

3. 拓展

那么由相机位姿(camera pose)和空间点（land mark）构成状态变量的，在最小重投影误差时的求解方程，对应的信息矩阵是什么呢？（信息矩阵H的一般构建形式： ）

参考vio课程：第4节 滑动窗口算法理论：VIO融合及其可观性与一致性

Eigen::Matrix<double,2,3> jacobian_uv_Pc; 
jacobian_uv_Pc<< fx/z, 0 , -x * fx/z_2,
        0, fy/z, -y * fy/z_2;

// 重投影误差对 landmark 的求导 对应上述公式(7.47)
Eigen::Matrix<double,2,3> jacobian_Pj = jacobian_uv_Pc * Rcw; 

// 重投影误差对 camera pose 的求导，
// SLAM十四讲中，基本对于上述公式(7.45): 这里的前三列在后，后三列在前
Eigen::Matrix<double,2,6> jacobian_Ti; 
jacobian_Ti << -x* y * fx/z_2, (1+ x*x/z_2)*fx, -y/z*fx, fx/z, 0 , -x * fx/z_2,
                -(1+y*y/z_2)*fy, x*y/z_2 * fy, x/z * fy, 0,fy/z, -y * fy/z_2;

// camera pose 和 camera pose 之间的信息矩阵： 
H.block(i*6,i*6,6,6) += jacobian_Ti.transpose() * jacobian_Ti;

// landmark 和 landmark 之间的信息矩阵
H.block(j*3 + 6*poseNums,j*3 + 6*poseNums,3,3) += jacobian_Tj.transpose() * jacobian_Tj;

// camera pose 和 landmark 之间的信息矩阵
H.block(i*6,j*3 + 6*poseNums, 6,3) += jacobian_Ti.transpose() * jacobian_Pj;

// landmark 和 camera pose 之间的信息矩阵
H.block(j*3 + 6*poseNums,i*6 , 3,6) += jacobian_Pj.transpose() * jacobian_Ti; 

相关文章：SLAM_BA中重投影误差e 关于相机位姿扰动量δξ 的雅克比矩阵J 公式推导_惊鸿一博的博客-CSDN博客