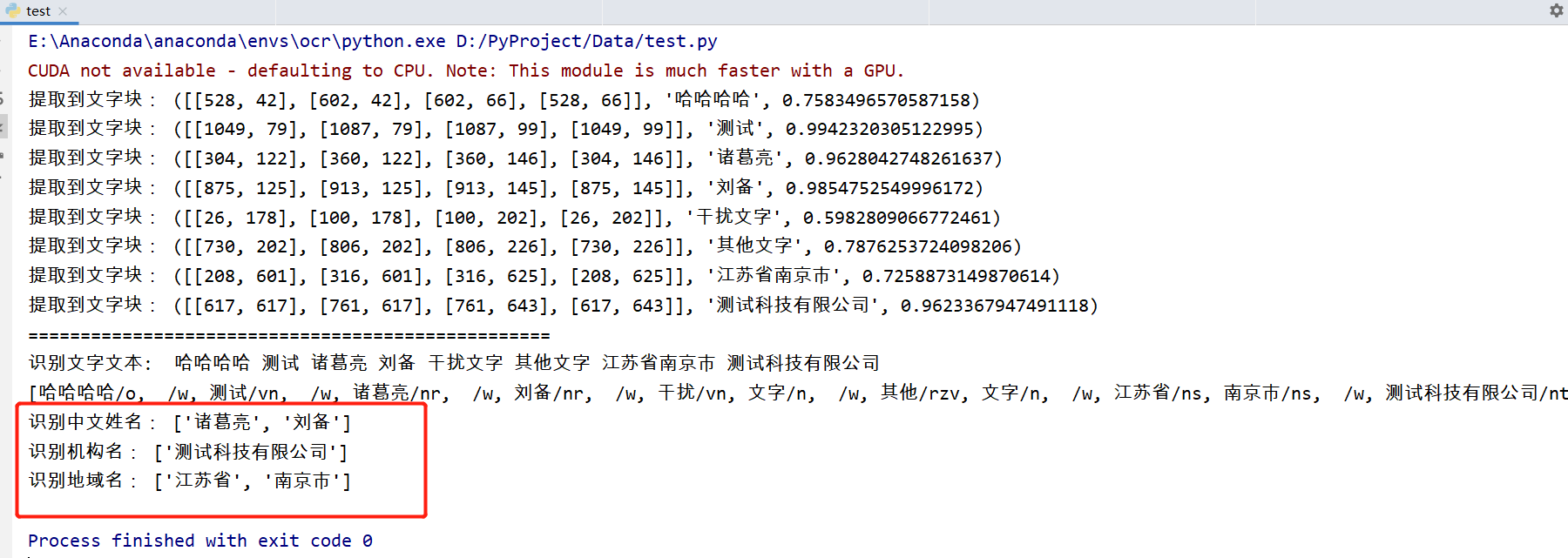
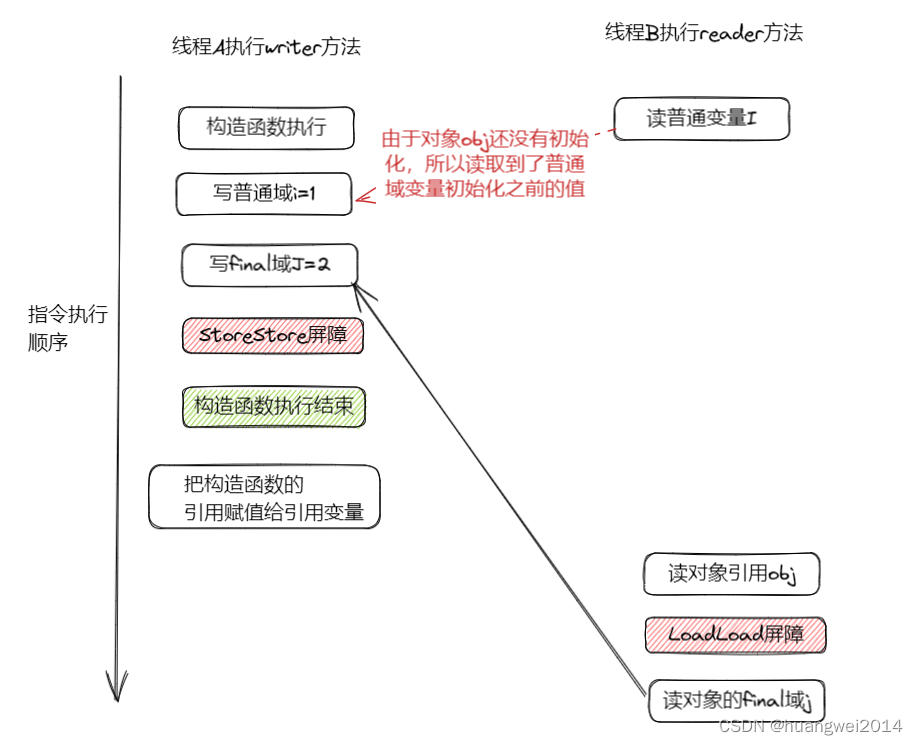
本文重点

前面我们学习了降维算法的两大应用场景，本节课程我们将学习具体的降维算法PCA，它是主成分分析法。

PCA要做什么？

将二维数据降维到一维，关键就是找到一个方向向量，然后把所有的数据都投射到该向量上，那么什么样的方向向量最好呢？

我们希望投射平均均方误差能尽可能的小，也就是说希望下图中的红色小线段（投影误差）的平方和达到最小值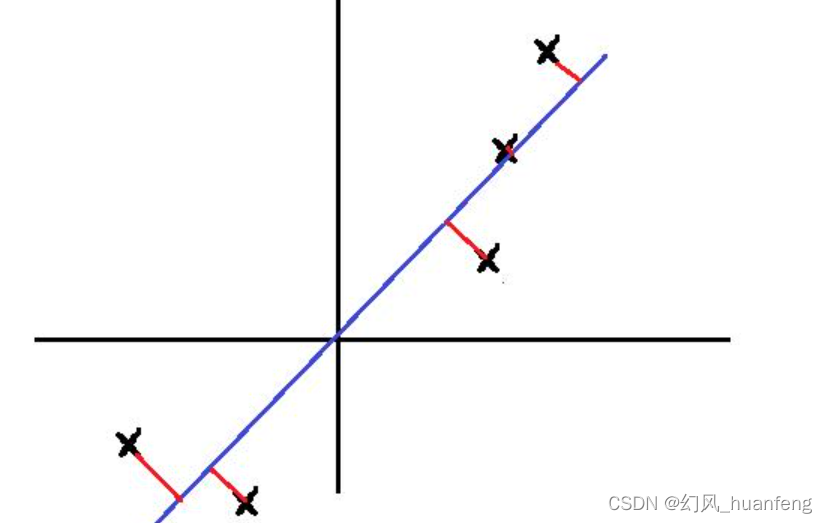

 

蓝色线就是方向向量

PCA就是要找到使得投影误差和最小的k维平面，然后样本对其做投影，从而达到降维的目的。需要注意的一点是在应用PCA之前，通常的做法是：先进行均值归一化和特征规范化，使得特征x1和x2均值为0，数值在可比较的范围之内。

n维降低到k维

数据从二维降到一维，那么我们需要找一个方向向量，更一般的是如果我们有n维的数据降到k维，那么这种情况下，我们需要找到k个方向向量来对数据进行投影，从而最小化投影误差。

比如三维降到二维，那么我们就要找到2个向量（组成平面），然后让所有的样本点映射到这个平面，所以n维降到k维，目标就是找到k个向量μ(1)、μ(2)、μ(3)…μ(k),我们要做的就是将数据投影到这k个向量展开的线性子空间上，使得总的投射误差最小。

主成分分析与线性回归的比较

主成分分析与线性回归是两种不同的算法。