首先可以将方程两边同时加上x,,这时候两边同时再除以1+x,就得到了
,变形为
。(变性后的迭代式不唯一,这里随便选取一个)
当x是准确值的时候,两边应该是相等的,如果x是近似值,x误差很小很小,我们变可以认为x是可接受的近似解。
因此可以构造迭代式:
根据上面的迭代式,可以得到一个x值的序列:,这个序列中的每一个值都应该比前面的值更加接近x的精确值, 关于什么是不动点迭代法这里大致介绍一下:


详细请参考:第四章:方程求根的迭代法 - 简书 (jianshu.com)中的4.2
#include<stdio.h>
#include<math.h>
#define PRECISION 0.000001
int main()
{
//用迭代法计算方程x^2=a的解,即计算根号a的值(不用库函数)
float a,x=1.0,temp;
int count=0;
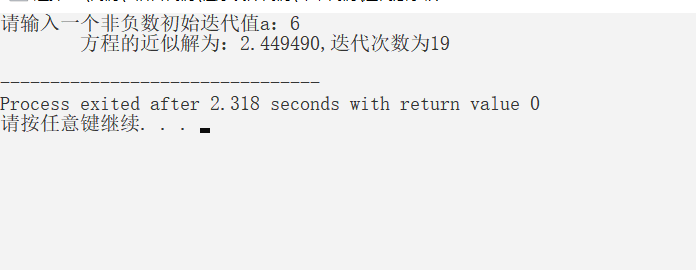
printf("请输入一个非负数初始迭代值a:");
scanf("%f",&a);
do
{
temp=x;
x=1+(a-1)/(x+1);
count++;
}while(fabs(x-temp)>=PRECISION);
printf("\t方程的近似解为:%f,迭代次数为%d\n",x,count);
return 0;
}