文章目录

KNN算法
- 前言距离度量
- - (1) 欧式距离
  - (2) 曼哈顿距离(Manhattan distance)
  - (3) 切比雪夫距离(Chebyshev distance)
  - (4) 闵可夫斯基距离(Minkowski distance)
  - (5) 汉明距离(Hamming distance)
  - (6) 余弦相似度(Cosine Similarity)
- KNN算法介绍
- - 1 数据的准备
  - 2 划分训练数据和测试数据
  - 3 通过K个近邻预测的标签的距离来预测当前样本的标签
  - 4 计算准确率
- 试试Scikit-learn
- - - sklearn.neighbors.KNeighborsClassifier
实验1 试试用KNN完成回归任务
- - 1 准备数据
  - 2 通过K个近邻预测的标签的距离来预测当前样本的标签
  - 3 通过R方进行评估

KNN算法

1． $k$ 近邻法是基本且简单的分类与回归方法。 $k$ 近邻法的基本做法是：对给定的训练实例点和输入实例点，首先确定输入实例点的 $k$ 个最近邻训练实例点，然后利用这 $k$ 个训练实例点的类的多数来预测输入实例点的类。

2． $k$ 近邻模型对应于基于训练数据集对特征空间的一个划分。 $k$ 近邻法中，当训练集、距离度量、 $k$ 值及分类决策规则确定后，其结果唯一确定，没有近似，他没有学习参数。

3． $k$ 近邻法三要素：距离度量、 $k$ 值的选择和分类决策规则。常用的距离度量是欧氏距离及更一般的pL距离。 $k$ 值小时， $k$ 近邻模型更复杂； $k$ 值大时， $k$ 近邻模型更简单。 $k$ 值的选择反映了对近似误差与估计误差之间的权衡，通常由交叉验证选择最优的 $k$ 。

常用的分类决策规则是多数表决，对应于经验风险最小化。

4． $k$ 近邻法的实现需要考虑如何快速搜索k个最近邻点。kd树是一种便于对k维空间中的数据进行快速检索的数据结构。kd树是二叉树，表示对 $k$ 维空间的一个划分，其每个结点对应于 $k$ 维空间划分中的一个超矩形区域。利用kd树可以省去对大部分数据点的搜索，从而减少搜索的计算量。

前言距离度量

在机器学习算法中，我们经常需要计算样本之间的相似度，通常的做法是计算样本之间的距离。

设 $x$ 和 $y$ 为两个向量，求它们之间的距离。

这里用Numpy实现，设和为ndarray <numpy.ndarray>，它们的shape都是(N,)

$d$ 为所求的距离，是个浮点数（float）。

(1) 欧式距离

欧几里得度量(euclidean metric)(也称欧氏距离)是一个通常采用的距离定义，指在 $m$ 维空间中两个点之间的真实距离，或者向量的自然长度(即该点到原点的距离)。在二维和三维空间中的欧氏距离就是两点之间的实际距离。

距离公式：

$d\left( x,y \right) = \sqrt{\sum_{i}^{}(x_{i} - y_{i})^{2}}$

代码实现：

def euclidean(x, y):
    return np.sqrt(np.sum((x - y)**2))

(2) 曼哈顿距离(Manhattan distance)

想象你在城市道路里，要从一个十字路口开车到另外一个十字路口，驾驶距离是两点间的直线距离吗？显然不是，除非你能穿越大楼。实际驾驶距离就是这个“曼哈顿距离”。而这也是曼哈顿距离名称的来源，曼哈顿距离也称为城市街区距离(City Block distance)。

距离公式：
$\sum_{i}^{}|x_{i} - y_{i}|$

代码实现：

def manhatan_distance(x,y):
    return np.sum(np.abs(x-y))

(3) 切比雪夫距离(Chebyshev distance)

在数学中，切比雪夫距离(Chebyshev distance)或是L∞度量，是向量空间中的一种度量，二个点之间的距离定义是其各坐标数值差绝对值的最大值。以数学的观点来看，切比雪夫距离是由一致范数(uniform norm)(或称为上确界范数)所衍生的度量，也是超凸度量(injective metric space)的一种。

距离公式：

$d\left( x,y \right) = \max_{i}\left| x_{i} - y_{i} \right|$

若将国际象棋棋盘放在二维直角座标系中，格子的边长定义为1，座标的 $x$ 轴及 $y$ 轴和棋盘方格平行，原点恰落在某一格的中心点，则王从一个位置走到其他位置需要的步数恰为二个位置的切比雪夫距离，因此切比雪夫距离也称为棋盘距离。例如位置F6和位置E2的切比雪夫距离为4。任何一个不在棋盘边缘的位置，和周围八个位置的切比雪夫距离都是1。

代码实现：

def chebysev_distance(x,y):
    return np.max(np.abs(x-y))

(4) 闵可夫斯基距离(Minkowski distance)

闵氏空间指狭义相对论中由一个时间维和三个空间维组成的时空，为俄裔德国数学家闵可夫斯基(H.Minkowski,1864-1909)最先表述。他的平坦空间(即假设没有重力，曲率为零的空间)的概念以及表示为特殊距离量的几何学是与狭义相对论的要求相一致的。闵可夫斯基空间不同于牛顿力学的平坦空间。 $p$ 取1或2时的闵氏距离是最为常用的， $p = 2$ 即为欧氏距离，而 $p = 1$ 时则为曼哈顿距离。

当 $p$ 取无穷时的极限情况下，可以得到切比雪夫距离。

距离公式：

$d\left( x,y \right) = \left( \sum_{i}^{}|x_{i} - y_{i}|^{p} \right)^{\frac{1}{p}}$

代码实现：

def minkowski(x, y, p):
    return np.sum(np.abs(x - y)**p)**(1 / p)

(5) 汉明距离(Hamming distance)

汉明距离是使用在数据传输差错控制编码里面的，汉明距离是一个概念，它表示两个(相同长度)字对应位不同的数量，我们以表示两个字,之间的汉明距离。对两个字符串进行异或运算，并统计结果为1的个数，那么这个数就是汉明距离。

距离公式：

$d\left( x,y \right) = \frac{1}{N}\sum_{i}^{}1_{x_{i} \neq y_{i}}$

def hamming(x,y):
    return np.sum(x!=y)/len(x)

(6) 余弦相似度(Cosine Similarity)

余弦相似性通过测量两个向量的夹角的余弦值来度量它们之间的相似性。0度角的余弦值是1，而其他任何角度的余弦值都不大于1；并且其最小值是-1。从而两个向量之间的角度的余弦值确定两个向量是否大致指向相同的方向。两个向量有相同的指向时，余弦相似度的值为1；两个向量夹角为90°时，余弦相似度的值为0；两个向量指向完全相反的方向时，余弦相似度的值为-1。这结果是与向量的长度无关的，仅仅与向量的指向方向相关。余弦相似度通常用于正空间，因此给出的值为0到1之间。

二维空间为例，上图的 $a$ 和 $b$ 是两个向量，我们要计算它们的夹角θ。余弦定理告诉我们，可以用下面的公式求得：

$\cos\theta = \frac{a^{2} + b^{2} - c^{2}}{2ab}$

假定 $a$ 向量是 $\left\lbrack x_{1},y_{1} \right\rbrack$ ， $b$ 向量是 $\left\lbrack x_{2},y_{2} \right\rbrack$ ，两个向量间的余弦值可以通过使用欧几里得点积公式求出：

$\cos\left( \theta \right) = \frac{A \cdot B}{\parallel A \parallel \parallel B \parallel} = \frac{\sum_{i = 1}^{n}A_{i} \times B_{i}}{\sqrt{\sum_{i = 1}^{n}(A_{i})^{2} \times \sqrt{\sum_{i = 1}^{n}(B_{i})^{2}}}}$

$\cos\left( \theta \right) = \frac{A \cdot B}{\parallel A \parallel \parallel B \parallel} = \frac{\left( x_{1},y_{1} \right) \cdot \left( x_{2},y_{2} \right)}{\sqrt{x_{1}^{2} + y_{1}^{2}} \times \sqrt{x_{2}^{2} + y_{2}^{2}}} = \frac{x_{1}x_{2} + y_{1}y_{2}}{\sqrt{x_{1}^{2} + y_{1}^{2}} \times \sqrt{x_{2}^{2} + y_{2}^{2}}}$

如果向量 $a$ 和 $b$ 不是二维而是 $n$ 维，上述余弦的计算法仍然正确。假定 $A$ 和 $B$ 是两个 $n$ 维向量， $A$ 是 $\left\lbrack A_{1},A_{2},\ldots,A_{n} \right\rbrack$ ， $B$ 是 $\left\lbrack B_{1},B_{2},\ldots,B_{n} \right\rbrack$ ，则 $A$ 与 $B$ 的夹角余弦等于：

$\cos\left( \theta \right) = \frac{A \cdot B}{\parallel A \parallel \parallel B \parallel} = \frac{\sum_{i = 1}^{n}A_{i} \times B_{i}}{\sqrt{\sum_{i = 1}^{n}(A_{i})^{2}} \times \sqrt{\sum_{i = 1}^{n}(B_{i})^{2}}}$

代码实现：

def square_rooted(x):
    return np.sqrt(np.sum(np.power(x,2)))

def cosine_similarity_distance(x,y):
    fenzi=np.sum(np.multiply(x,y))
    fenmu=square_rooted(x)*square_rooted(y)
    return fenzi/fenmu

import numpy as np
print(cosine_similarity_distance([3, 45, 7, 2], [2, 54, 13, 15]))

0.9722842517123499

KNN算法介绍

2． $k$ 近邻模型对应于基于训练数据集对特征空间的一个划分。 $k$ 近邻法中，当训练集、距离度量、 $k$ 值及分类决策规则确定后，其结果唯一确定。

3． $k$ 近邻法三要素：距离度量、 $k$ 值的选择和分类决策规则。常用的距离度量是欧氏距离。 $k$ 值小时， $k$ 近邻模型更复杂； $k$ 值大时， $k$ 近邻模型更简单。 $k$ 值的选择反映了对近似误差与估计误差之间的权衡，通常由交叉验证选择最优的 $k$ 。

常用的分类决策规则是多数表决，对应于经验风险最小化。

python实现，遍历所有数据点，找出 $n$ 个距离最近的点的分类情况，少数服从多数

1 数据的准备

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from collections import Counter

导入鸢尾花数据集

iris = load_iris()
iris

{'data': array([[5.1, 3.5, 1.4, 0.2],
        [4.9, 3. , 1.4, 0.2],
        [4.7, 3.2, 1.3, 0.2],
        [4.6, 3.1, 1.5, 0.2],
        [5. , 3.6, 1.4, 0.2],
        [5.4, 3.9, 1.7, 0.4],
        [4.6, 3.4, 1.4, 0.3],
        [5. , 3.4, 1.5, 0.2],
        [4.4, 2.9, 1.4, 0.2],
        [4.9, 3.1, 1.5, 0.1],
        [5.4, 3.7, 1.5, 0.2],
        [4.8, 3.4, 1.6, 0.2],
        [4.8, 3. , 1.4, 0.1],
        [4.3, 3. , 1.1, 0.1],
        [5.8, 4. , 1.2, 0.2],
        [5.7, 4.4, 1.5, 0.4],
        [5.4, 3.9, 1.3, 0.4],
        [5.1, 3.5, 1.4, 0.3],
        [5.7, 3.8, 1.7, 0.3],
        [5.1, 3.8, 1.5, 0.3],
        [5.4, 3.4, 1.7, 0.2],
        [5.1, 3.7, 1.5, 0.4],
        [4.6, 3.6, 1. , 0.2],
        [5.1, 3.3, 1.7, 0.5],
        [4.8, 3.4, 1.9, 0.2],
        [5. , 3. , 1.6, 0.2],
        [5. , 3.4, 1.6, 0.4],
        [5.2, 3.5, 1.5, 0.2],
        [5.2, 3.4, 1.4, 0.2],
        [4.7, 3.2, 1.6, 0.2],
        [4.8, 3.1, 1.6, 0.2],
        [5.4, 3.4, 1.5, 0.4],
        [5.2, 4.1, 1.5, 0.1],
        [5.5, 4.2, 1.4, 0.2],
        [4.9, 3.1, 1.5, 0.2],
        [5. , 3.2, 1.2, 0.2],
        [5.5, 3.5, 1.3, 0.2],
        [4.9, 3.6, 1.4, 0.1],
        [4.4, 3. , 1.3, 0.2],
        [5.1, 3.4, 1.5, 0.2],
        [5. , 3.5, 1.3, 0.3],
        [4.5, 2.3, 1.3, 0.3],
        [4.4, 3.2, 1.3, 0.2],
        [5. , 3.5, 1.6, 0.6],
        [5.1, 3.8, 1.9, 0.4],
        [4.8, 3. , 1.4, 0.3],
        [5.1, 3.8, 1.6, 0.2],
        [4.6, 3.2, 1.4, 0.2],
        [5.3, 3.7, 1.5, 0.2],
        [5. , 3.3, 1.4, 0.2],
        [7. , 3.2, 4.7, 1.4],
        [6.4, 3.2, 4.5, 1.5],
        [6.9, 3.1, 4.9, 1.5],
        [5.5, 2.3, 4. , 1.3],
        [6.5, 2.8, 4.6, 1.5],
        [5.7, 2.8, 4.5, 1.3],
        [6.3, 3.3, 4.7, 1.6],
        [4.9, 2.4, 3.3, 1. ],
        [6.6, 2.9, 4.6, 1.3],
        [5.2, 2.7, 3.9, 1.4],
        [5. , 2. , 3.5, 1. ],
        [5.9, 3. , 4.2, 1.5],
        [6. , 2.2, 4. , 1. ],
        [6.1, 2.9, 4.7, 1.4],
        [5.6, 2.9, 3.6, 1.3],
        [6.7, 3.1, 4.4, 1.4],
        [5.6, 3. , 4.5, 1.5],
        [5.8, 2.7, 4.1, 1. ],
        [6.2, 2.2, 4.5, 1.5],
        [5.6, 2.5, 3.9, 1.1],
        [5.9, 3.2, 4.8, 1.8],
        [6.1, 2.8, 4. , 1.3],
        [6.3, 2.5, 4.9, 1.5],
        [6.1, 2.8, 4.7, 1.2],
        [6.4, 2.9, 4.3, 1.3],
        [6.6, 3. , 4.4, 1.4],
        [6.8, 2.8, 4.8, 1.4],
        [6.7, 3. , 5. , 1.7],
        [6. , 2.9, 4.5, 1.5],
        [5.7, 2.6, 3.5, 1. ],
        [5.5, 2.4, 3.8, 1.1],
        [5.5, 2.4, 3.7, 1. ],
        [5.8, 2.7, 3.9, 1.2],
        [6. , 2.7, 5.1, 1.6],
        [5.4, 3. , 4.5, 1.5],
        [6. , 3.4, 4.5, 1.6],
        [6.7, 3.1, 4.7, 1.5],
        [6.3, 2.3, 4.4, 1.3],
        [5.6, 3. , 4.1, 1.3],
        [5.5, 2.5, 4. , 1.3],
        [5.5, 2.6, 4.4, 1.2],
        [6.1, 3. , 4.6, 1.4],
        [5.8, 2.6, 4. , 1.2],
        [5. , 2.3, 3.3, 1. ],
        [5.6, 2.7, 4.2, 1.3],
        [5.7, 3. , 4.2, 1.2],
        [5.7, 2.9, 4.2, 1.3],
        [6.2, 2.9, 4.3, 1.3],
        [5.1, 2.5, 3. , 1.1],
        [5.7, 2.8, 4.1, 1.3],
        [6.3, 3.3, 6. , 2.5],
        [5.8, 2.7, 5.1, 1.9],
        [7.1, 3. , 5.9, 2.1],
        [6.3, 2.9, 5.6, 1.8],
        [6.5, 3. , 5.8, 2.2],
        [7.6, 3. , 6.6, 2.1],
        [4.9, 2.5, 4.5, 1.7],
        [7.3, 2.9, 6.3, 1.8],
        [6.7, 2.5, 5.8, 1.8],
        [7.2, 3.6, 6.1, 2.5],
        [6.5, 3.2, 5.1, 2. ],
        [6.4, 2.7, 5.3, 1.9],
        [6.8, 3. , 5.5, 2.1],
        [5.7, 2.5, 5. , 2. ],
        [5.8, 2.8, 5.1, 2.4],
        [6.4, 3.2, 5.3, 2.3],
        [6.5, 3. , 5.5, 1.8],
        [7.7, 3.8, 6.7, 2.2],
        [7.7, 2.6, 6.9, 2.3],
        [6. , 2.2, 5. , 1.5],
        [6.9, 3.2, 5.7, 2.3],
        [5.6, 2.8, 4.9, 2. ],
        [7.7, 2.8, 6.7, 2. ],
        [6.3, 2.7, 4.9, 1.8],
        [6.7, 3.3, 5.7, 2.1],
        [7.2, 3.2, 6. , 1.8],
        [6.2, 2.8, 4.8, 1.8],
        [6.1, 3. , 4.9, 1.8],
        [6.4, 2.8, 5.6, 2.1],
        [7.2, 3. , 5.8, 1.6],
        [7.4, 2.8, 6.1, 1.9],
        [7.9, 3.8, 6.4, 2. ],
        [6.4, 2.8, 5.6, 2.2],
        [6.3, 2.8, 5.1, 1.5],
        [6.1, 2.6, 5.6, 1.4],
        [7.7, 3. , 6.1, 2.3],
        [6.3, 3.4, 5.6, 2.4],
        [6.4, 3.1, 5.5, 1.8],
        [6. , 3. , 4.8, 1.8],
        [6.9, 3.1, 5.4, 2.1],
        [6.7, 3.1, 5.6, 2.4],
        [6.9, 3.1, 5.1, 2.3],
        [5.8, 2.7, 5.1, 1.9],
        [6.8, 3.2, 5.9, 2.3],
        [6.7, 3.3, 5.7, 2.5],
        [6.7, 3. , 5.2, 2.3],
        [6.3, 2.5, 5. , 1.9],
        [6.5, 3. , 5.2, 2. ],
        [6.2, 3.4, 5.4, 2.3],
        [5.9, 3. , 5.1, 1.8]]),
 'target': array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
        0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
        0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
        1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
        1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
        2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
        2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2]),
 'frame': None,
 'target_names': array(['setosa', 'versicolor', 'virginica'], dtype='<U10'),
 'DESCR': '.. _iris_dataset:\n\nIris plants dataset\n--------------------\n\n**Data Set Characteristics:**\n\n    :Number of Instances: 150 (50 in each of three classes)\n    :Number of Attributes: 4 numeric, predictive attributes and the class\n    :Attribute Information:\n        - sepal length in cm\n        - sepal width in cm\n        - petal length in cm\n        - petal width in cm\n        - class:\n                - Iris-Setosa\n                - Iris-Versicolour\n                - Iris-Virginica\n                \n    :Summary Statistics:\n\n    ============== ==== ==== ======= ===== ====================\n                    Min  Max   Mean    SD   Class Correlation\n    ============== ==== ==== ======= ===== ====================\n    sepal length:   4.3  7.9   5.84   0.83    0.7826\n    sepal width:    2.0  4.4   3.05   0.43   -0.4194\n    petal length:   1.0  6.9   3.76   1.76    0.9490  (high!)\n    petal width:    0.1  2.5   1.20   0.76    0.9565  (high!)\n    ============== ==== ==== ======= ===== ====================\n\n    :Missing Attribute Values: None\n    :Class Distribution: 33.3% for each of 3 classes.\n    :Creator: R.A. Fisher\n    :Donor: Michael Marshall (MARSHALL%PLU@io.arc.nasa.gov)\n    :Date: July, 1988\n\nThe famous Iris database, first used by Sir R.A. Fisher. The dataset is taken\nfrom Fisher\'s paper. Note that it\'s the same as in R, but not as in the UCI\nMachine Learning Repository, which has two wrong data points.\n\nThis is perhaps the best known database to be found in the\npattern recognition literature.  Fisher\'s paper is a classic in the field and\nis referenced frequently to this day.  (See Duda & Hart, for example.)  The\ndata set contains 3 classes of 50 instances each, where each class refers to a\ntype of iris plant.  One class is linearly separable from the other 2; the\nlatter are NOT linearly separable from each other.\n\n.. topic:: References\n\n   - Fisher, R.A. "The use of multiple measurements in taxonomic problems"\n     Annual Eugenics, 7, Part II, 179-188 (1936); also in "Contributions to\n     Mathematical Statistics" (John Wiley, NY, 1950).\n   - Duda, R.O., & Hart, P.E. (1973) Pattern Classification and Scene Analysis.\n     (Q327.D83) John Wiley & Sons.  ISBN 0-471-22361-1.  See page 218.\n   - Dasarathy, B.V. (1980) "Nosing Around the Neighborhood: A New System\n     Structure and Classification Rule for Recognition in Partially Exposed\n     Environments".  IEEE Transactions on Pattern Analysis and Machine\n     Intelligence, Vol. PAMI-2, No. 1, 67-71.\n   - Gates, G.W. (1972) "The Reduced Nearest Neighbor Rule".  IEEE Transactions\n     on Information Theory, May 1972, 431-433.\n   - See also: 1988 MLC Proceedings, 54-64.  Cheeseman et al"s AUTOCLASS II\n     conceptual clustering system finds 3 classes in the data.\n   - Many, many more ...',
 'feature_names': ['sepal length (cm)',
  'sepal width (cm)',
  'petal length (cm)',
  'petal width (cm)'],
 'filename': 'iris.csv',
 'data_module': 'sklearn.datasets.data'}

iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df["target"]=iris.target
df.columns=iris.feature_names+["target"]
df

	sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)	target
0	5.1	3.5	1.4	0.2	0
1	4.9	3.0	1.4	0.2	0
2	4.7	3.2	1.3	0.2	0
3	4.6	3.1	1.5	0.2	0
4	5.0	3.6	1.4	0.2	0
...	...	...	...	...	...
145	6.7	3.0	5.2	2.3	2
146	6.3	2.5	5.0	1.9	2
147	6.5	3.0	5.2	2.0	2
148	6.2	3.4	5.4	2.3	2
149	5.9	3.0	5.1	1.8	2

150 rows × 5 columns

df.head()

	sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)
0	5.1	3.5	1.4	0.2
1	4.9	3.0	1.4	0.2
2	4.7	3.2	1.3	0.2
3	4.6	3.1	1.5	0.2
4	5.0	3.6	1.4	0.2

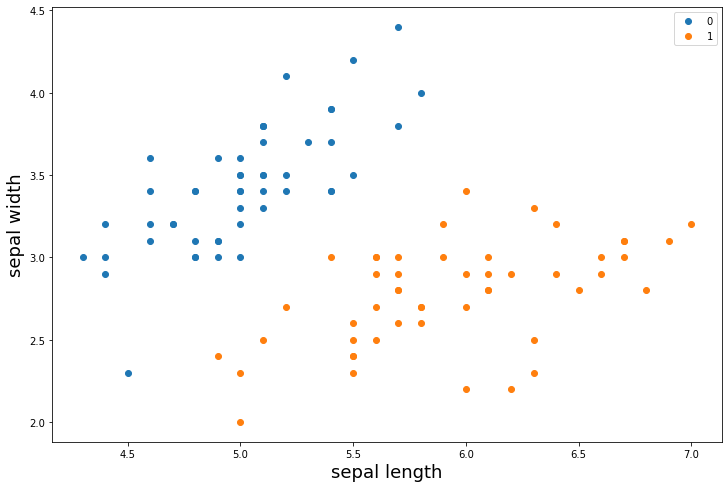
选择长和宽的数据进行可视化

#选取前100行数据进行可视化
plt.figure(figsize=(12, 8))
plt.scatter(df[:50]["sepal length (cm)"], df[:50]["sepal width (cm)"], label='0')
plt.scatter(df[50:100]["sepal length (cm)"], df[50:100]["sepal width (cm)"], label='1')
plt.xlabel('sepal length', fontsize=18)
plt.ylabel('sepal width', fontsize=18)
plt.legend()
plt.show()

2 划分训练数据和测试数据

from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test=train_test_split(df.iloc[:100,:2].values,df.iloc[:100,-1].values)
X_train.shape,X_test.shape,y_train.shape,y_test.shape

((75, 2), (25, 2), (75,), (25,))

X_train,y_train

(array([[5. , 3.3],
        [4.6, 3.4],
        [5.2, 4.1],
        [5.7, 2.8],
        [5.1, 3.4],
        [4.8, 3. ],
        [5.9, 3.2],
        [5.7, 3.8],
        [4.8, 3.4],
        [5.3, 3.7],
        [5.1, 3.8],
        [5.5, 2.4],
        [6. , 2.2],
        [5.5, 4.2],
        [5.5, 2.6],
        [5.4, 3.4],
        [4.4, 2.9],
        [6. , 2.9],
        [5.8, 2.7],
        [4.4, 3.2],
        [5.6, 2.9],
        [5.8, 2.7],
        [6.7, 3.1],
        [6. , 2.7],
        [5.7, 2.9],
        [4.6, 3.2],
        [4.9, 3.1],
        [7. , 3.2],
        [4.7, 3.2],
        [5.1, 2.5],
        [6.3, 2.3],
        [4.6, 3.1],
        [6.4, 3.2],
        [6.6, 3. ],
        [4.6, 3.6],
        [5.5, 2.4],
        [5.6, 3. ],
        [5.1, 3.7],
        [6.1, 2.8],
        [5.6, 2.7],
        [4.8, 3.1],
        [4.8, 3. ],
        [5. , 3.5],
        [6.2, 2.2],
        [6. , 3.4],
        [5.1, 3.3],
        [5.4, 3.9],
        [5.7, 2.6],
        [6.7, 3.1],
        [4.5, 2.3],
        [4.8, 3.4],
        [4.9, 2.4],
        [5.8, 4. ],
        [5. , 3. ],
        [6.6, 2.9],
        [6.1, 2.9],
        [5. , 3.5],
        [6.8, 2.8],
        [5. , 2.3],
        [5.4, 3. ],
        [4.3, 3. ],
        [4.9, 3.1],
        [4.9, 3. ],
        [5.1, 3.8],
        [5.1, 3.5],
        [5.5, 2.5],
        [5. , 3.6],
        [5. , 3.4],
        [5.4, 3.9],
        [5.1, 3.8],
        [5.1, 3.5],
        [5.2, 3.5],
        [5.8, 2.6],
        [6.4, 2.9],
        [6.1, 2.8]]),
 array([0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 1,
        1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1,
        1, 0, 0, 1, 1, 0, 0, 1, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1,
        0, 0, 0, 0, 0, 0, 1, 1, 1]))

3 通过K个近邻预测的标签的距离来预测当前样本的标签

#定义邻居数量
from collections import Counter
K=3

KNN_x=[]

for i in range(X_train.shape[0]):
    if len(KNN_x)<K:
        KNN_x.append((euclidean(X_test[0],X_train[i]),y_train[i]))

KNN_x

[(0.6324555320336757, 0), (0.9219544457292889, 0), (1.3999999999999995, 0)]

count=Counter([item[1] for item in KNN_x])
count

Counter({0: 3})

count.items()

dict_items([(0, 3)])

sorted(count.items(),key=lambda x:x[1])[-1][0]

#返回任意一个样本x的标签
def calcu_distance_return(x,X_train,y_train):
    KNN_x=[]
    #遍历训练集中的每个样本
    for i in range(X_train.shape[0]):
        if len(KNN_x)<K:
            KNN_x.append((euclidean(x,X_train[i]),y_train[i]))
        else:
            KNN_x.sort()
            for j in range(K): 
                if (euclidean(x,X_train[i]))< KNN_x[j][0]:
                    KNN_x[j]=(euclidean(x,X_train[i]),y_train[i])
                    break
    knn_label=[item[1] for item in KNN_x]           
    counter_knn=Counter(knn_label) 
    return sorted(counter_knn.items(),key=lambda item:item[1])[-1][0]

#对整个测试集进行预测
def predict(X_test):
    y_pred=np.zeros(X_test.shape[0])
    for i in range(X_test.shape[0]):
        y_hat_i=calcu_distance_return(X_test[i],X_train,y_train) 
        y_pred[i]=y_hat_i
    return y_pred

4 计算准确率

#输出预测结果
y_pred= predict(X_test).astype("int32")

y_pred

array([1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 1,
       1, 1, 0])

y_test=y_test.astype("int32")
y_test

array([1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 1,
       1, 1, 0])

#计算准确率
np.sum(y_pred==y_test)/X_test.shape[0]

1.0

试试Scikit-learn

sklearn.neighbors.KNeighborsClassifier

n_neighbors: 临近点个数，即k的个数，默认是5
p: 距离度量，默认
algorithm: 近邻算法，可选{‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’}
weights: 确定近邻的权重
n_neighbors ： int，optional(default = 5)
默认情况下kneighbors查询使用的邻居数。就是k-NN的k的值，选取最近的k个点。
weights ： str或callable，可选(默认=‘uniform’)
默认是uniform，参数可以是uniform、distance，也可以是用户自己定义的函数。uniform是均等的权重，就说所有的邻近点的权重都是相等的。distance是不均等的权重，距离近的点比距离远的点的影响大。用户自定义的函数，接收距离的数组，返回一组维数相同的权重。
algorithm ： {‘auto’，‘ball_tree’，‘kd_tree’，‘brute’}，可选
快速k近邻搜索算法，默认参数为auto，可以理解为算法自己决定合适的搜索算法。除此之外，用户也可以自己指定搜索算法ball_tree、kd_tree、brute方法进行搜索，brute是蛮力搜索，也就是线性扫描，当训练集很大时，计算非常耗时。kd_tree，构造kd树存储数据以便对其进行快速检索的树形数据结构，kd树也就是数据结构中的二叉树。以中值切分构造的树，每个结点是一个超矩形，在维数小于20时效率高。ball tree是为了克服kd树高纬失效而发明的，其构造过程是以质心C和半径r分割样本空间，每个节点是一个超球体。
leaf_size ： int，optional(默认值= 30)
默认是30，这个是构造的kd树和ball树的大小。这个值的设置会影响树构建的速度和搜索速度，同样也影响着存储树所需的内存大小。需要根据问题的性质选择最优的大小。
p ：整数，可选(默认= 2)
距离度量公式。在上小结，我们使用欧氏距离公式进行距离度量。除此之外，还有其他的度量方法，例如曼哈顿距离。这个参数默认为2，也就是默认使用欧式距离公式进行距离度量。也可以设置为1，使用曼哈顿距离公式进行距离度量。
metric ：字符串或可调用，默认为’minkowski’
用于距离度量，默认度量是minkowski，也就是p=2的欧氏距离(欧几里德度量)。
metric_params ： dict，optional(默认=None)
距离公式的其他关键参数，这个可以不管，使用默认的None即可。
n_jobs ： int或None，可选(默认=None)
并行处理设置。默认为1，临近点搜索并行工作数。如果为-1，那么CPU的所有cores都用于并行工作。

# 1导入模块
from sklearn.neighbors import KNeighborsClassifier
# 2创建KNN近邻实例
knn=KNeighborsClassifier(n_neighbors=4)
# 3 拟合该模型
knn.fit(X_train,y_train)
# 4 得到分数
knn.score(X_test,y_test)

1.0

试试其他的近邻数量

# 1导入模块
from sklearn.neighbors import KNeighborsClassifier
# 2创建KNN近邻实例
knn=KNeighborsClassifier(n_neighbors=2)
# 3 拟合该模型
knn.fit(X_train,y_train)
# 4 得到分数
knn.score(X_test,y_test)

1.0

# 1导入模块
from sklearn.neighbors import KNeighborsClassifier
# 2创建KNN近邻实例
knn=KNeighborsClassifier(n_neighbors=6)
# 3 拟合该模型
knn.fit(X_train,y_train)
# 4 得到分数
knn.score(X_test,y_test)

1.0

#5 搜索一下什么样的邻居个数K是最好的，K的范围这里设置为1,10
from sklearn.model_selection import train_test_split
def getBestK(X_train,y_train,K):
    best_score=0
    best_k=1
    best_model=knn=KNeighborsClassifier(1)
    X_train_set,X_val,y_train_set,y_val=train_test_split(X_train,y_train,random_state=0)
    for num in range(1,K):
        knn=KNeighborsClassifier(num)
        knn.fit(X_train_set,y_train_set)
        score=round(knn.score(X_val,y_val),2)
        print(score,num)
        if score>best_score:
            best_k=num
            best_score=score
            best_model=knn
    return best_k,best_score,best_model

best_k,best_score,best_model=getBestK(X_train,y_train,11)

#5采用测试集查看经验风险
best_model.score(X_test,y_test)

1.0

上面选择的k是在一次对训练集的划分的验证集上选的参数，具有一定的偶然性，使得最后根据最高验证分数选出来的在测试集上的效果不佳

#6 试试交叉验证误差
from sklearn.model_selection import RepeatedKFold
rkf=RepeatedKFold(n_repeats=10,n_splits=5,random_state=42)
for i,(train_index,test_index) in enumerate(rkf.split(X_train)):
    print("train_index",train_index)
    print("test_index",test_index)
#     print("新的训练数据为",X_train[train_index],y_train[train_index])
#     print("新的验证数据为",X_train[test_index],y_train[test_index])

train_index [ 1  2  3  5  6  7  8 11 13 14 15 16 17 19 20 21 22 23 24 25 26 27 29 30
 31 32 33 36 37 38 39 40 41 43 44 45 46 47 48 50 51 52 53 54 55 56 57 58
 59 60 62 65 66 67 68 70 71 72 73 74]
test_index [ 0  4  9 10 12 18 28 34 35 42 49 61 63 64 69]
train_index [ 0  1  2  3  4  6  8  9 10 11 12 13 14 15 17 18 19 20 21 23 24 25 26 27
 28 29 32 34 35 36 37 38 41 42 43 46 48 49 50 51 52 53 54 55 57 59 60 61
 62 63 64 65 67 68 69 70 71 72 73 74]
test_index [ 5  7 16 22 30 31 33 39 40 44 45 47 56 58 66]
train_index [ 0  1  2  4  5  7  9 10 11 12 14 15 16 18 20 21 22 23 24 26 27 28 29 30
 31 32 33 34 35 37 39 40 41 42 43 44 45 46 47 48 49 51 52 55 56 57 58 59
 60 61 63 64 65 66 67 68 69 70 71 73]
test_index [ 3  6  8 13 17 19 25 36 38 50 53 54 62 72 74]
train_index [ 0  1  2  3  4  5  6  7  8  9 10 12 13 14 16 17 18 19 20 21 22 23 25 28
 29 30 31 33 34 35 36 37 38 39 40 42 44 45 47 49 50 51 52 53 54 56 58 59
 60 61 62 63 64 65 66 69 70 71 72 74]
test_index [11 15 24 26 27 32 41 43 46 48 55 57 67 68 73]
train_index [ 0  3  4  5  6  7  8  9 10 11 12 13 15 16 17 18 19 22 24 25 26 27 28 30
 31 32 33 34 35 36 38 39 40 41 42 43 44 45 46 47 48 49 50 53 54 55 56 57
 58 61 62 63 64 66 67 68 69 72 73 74]
test_index [ 1  2 14 20 21 23 29 37 51 52 59 60 65 70 71]
train_index [ 0  2  3  4  6  7  8  9 10 11 12 13 14 16 18 19 21 22 23 24 25 26 27 28
 30 32 33 34 35 36 37 38 39 40 41 42 43 44 47 48 50 52 53 54 55 56 57 58
 59 61 62 64 65 66 67 68 70 71 72 73]
test_index [ 1  5 15 17 20 29 31 45 46 49 51 60 63 69 74]
train_index [ 0  1  2  4  5  6  7  8 10 11 13 14 15 16 17 20 21 22 23 25 26 27 28 29
 31 32 33 34 35 36 38 39 40 41 43 44 45 46 49 50 51 52 53 54 55 56 57 59
 60 61 62 63 64 65 66 69 70 71 73 74]
test_index [ 3  9 12 18 19 24 30 37 42 47 48 58 67 68 72]
train_index [ 0  1  3  4  5  6  7  8  9 10 11 12 14 15 16 17 18 19 20 23 24 25 27 28
 29 30 31 32 34 37 38 40 41 42 43 44 45 46 47 48 49 50 51 52 56 57 58 59
 60 62 63 64 65 67 68 69 70 72 73 74]
test_index [ 2 13 21 22 26 33 35 36 39 53 54 55 61 66 71]
train_index [ 0  1  2  3  5  7  8  9 10 12 13 14 15 17 18 19 20 21 22 23 24 25 26 28
 29 30 31 33 35 36 37 39 40 42 43 44 45 46 47 48 49 51 52 53 54 55 58 59
 60 61 63 64 66 67 68 69 71 72 73 74]
test_index [ 4  6 11 16 27 32 34 38 41 50 56 57 62 65 70]
train_index [ 1  2  3  4  5  6  9 11 12 13 15 16 17 18 19 20 21 22 24 26 27 29 30 31
 32 33 34 35 36 37 38 39 41 42 45 46 47 48 49 50 51 53 54 55 56 57 58 60
 61 62 63 65 66 67 68 69 70 71 72 74]
test_index [ 0  7  8 10 14 23 25 28 40 43 44 52 59 64 73]
train_index [ 0  1  2  3  4  5  7  8 10 11 14 16 18 19 20 21 22 23 24 25 26 27 28 29
 31 32 35 36 38 39 40 41 42 43 45 46 47 48 49 50 51 52 53 54 55 56 57 58
 61 62 63 64 66 67 68 69 71 72 73 74]
test_index [ 6  9 12 13 15 17 30 33 34 37 44 59 60 65 70]
train_index [ 0  1  2  5  6  7  8  9 11 12 13 14 15 16 17 18 20 22 23 26 27 29 30 31
 32 33 34 36 37 38 40 41 43 44 45 47 48 50 51 53 54 55 56 57 58 59 60 61
 63 64 65 66 67 68 69 70 71 72 73 74]
test_index [ 3  4 10 19 21 24 25 28 35 39 42 46 49 52 62]
train_index [ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 17 19 21 23 24 25 26 27
 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 46 49 50 51 52 53 59
 60 61 62 63 65 66 68 69 70 71 73 74]
test_index [16 18 20 22 45 47 48 54 55 56 57 58 64 67 72]
train_index [ 0  2  3  4  5  6  7  9 10 12 13 15 16 17 18 19 20 21 22 24 25 26 27 28
 29 30 33 34 35 37 38 39 42 43 44 45 46 47 48 49 52 54 55 56 57 58 59 60
 61 62 64 65 66 67 68 69 70 72 73 74]
test_index [ 1  8 11 14 23 31 32 36 40 41 50 51 53 63 71]
train_index [ 1  3  4  6  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 28 30
 31 32 33 34 35 36 37 39 40 41 42 44 45 46 47 48 49 50 51 52 53 54 55 56
 57 58 59 60 62 63 64 65 67 70 71 72]
test_index [ 0  2  5  7 26 27 29 38 43 61 66 68 69 73 74]
train_index [ 0  1  2  3  4  6  7  8 10 11 13 15 17 18 19 20 21 22 23 24 25 27 28 29
 30 31 32 33 34 36 37 38 39 40 41 44 45 46 47 48 49 51 52 53 54 55 56 57
 59 60 61 66 67 68 69 70 71 72 73 74]
test_index [ 5  9 12 14 16 26 35 42 43 50 58 62 63 64 65]
train_index [ 0  1  2  4  5  6  7  8  9 10 11 12 14 15 16 18 19 22 23 24 25 26 29 30
 31 32 34 35 36 37 38 39 40 41 42 43 44 47 48 49 50 51 55 56 57 58 59 62
 63 64 65 66 67 68 69 70 71 72 73 74]
test_index [ 3 13 17 20 21 27 28 33 45 46 52 53 54 60 61]
train_index [ 0  1  3  4  5  6  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 25 26 27
 28 29 30 31 32 33 34 35 36 38 39 41 42 43 45 46 47 48 49 50 51 52 53 54
 55 56 58 60 61 62 63 64 65 67 70 71]
test_index [ 2  7 23 24 37 40 44 57 59 66 68 69 72 73 74]
train_index [ 0  2  3  5  7  9 10 12 13 14 16 17 18 19 20 21 22 23 24 26 27 28 29 30
 32 33 35 37 38 39 40 41 42 43 44 45 46 49 50 51 52 53 54 56 57 58 59 60
 61 62 63 64 65 66 68 69 70 72 73 74]
test_index [ 1  4  6  8 11 15 25 31 34 36 47 48 55 67 71]
train_index [ 1  2  3  4  5  6  7  8  9 11 12 13 14 15 16 17 20 21 23 24 25 26 27 28
 31 33 34 35 36 37 40 42 43 44 45 46 47 48 50 52 53 54 55 57 58 59 60 61
 62 63 64 65 66 67 68 69 71 72 73 74]
test_index [ 0 10 18 19 22 29 30 32 38 39 41 49 51 56 70]
train_index [ 0  1  2  3  4  5  7  8  9 13 14 16 17 18 20 21 22 23 24 25 26 27 28 29
 30 31 32 34 35 36 37 38 40 41 42 43 44 45 46 47 48 50 53 54 56 59 60 61
 63 64 65 66 67 68 69 70 71 72 73 74]
test_index [ 6 10 11 12 15 19 33 39 49 51 52 55 57 58 62]
train_index [ 2  3  4  5  6  7 10 11 12 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
 30 31 32 33 34 36 37 39 40 42 43 45 46 47 48 49 50 51 52 53 55 56 57 58
 59 60 61 62 63 64 65 66 67 69 72 74]
test_index [ 0  1  8  9 13 14 35 38 41 44 54 68 70 71 73]
train_index [ 0  1  3  4  5  6  7  8  9 10 11 12 13 14 15 16 18 19 20 26 27 28 29 32
 33 34 35 36 37 38 39 40 41 43 44 45 47 48 49 50 51 52 53 54 55 56 57 58
 59 60 62 63 65 66 68 69 70 71 73 74]
test_index [ 2 17 21 22 23 24 25 30 31 42 46 61 64 67 72]
train_index [ 0  1  2  4  6  7  8  9 10 11 12 13 14 15 17 19 20 21 22 23 24 25 26 27
 29 30 31 32 33 35 37 38 39 41 42 44 46 49 50 51 52 53 54 55 57 58 59 60
 61 62 63 64 67 68 69 70 71 72 73 74]
test_index [ 3  5 16 18 28 34 36 40 43 45 47 48 56 65 66]
train_index [ 0  1  2  3  5  6  8  9 10 11 12 13 14 15 16 17 18 19 21 22 23 24 25 28
 30 31 33 34 35 36 38 39 40 41 42 43 44 45 46 47 48 49 51 52 54 55 56 57
 58 61 62 64 65 66 67 68 70 71 72 73]
test_index [ 4  7 20 26 27 29 32 37 50 53 59 60 63 69 74]
train_index [ 0  1  3  4  5  7  8 11 12 13 14 15 16 18 19 20 21 22 23 24 25 26 27 28
 29 30 31 32 34 35 36 37 38 39 41 42 43 44 45 46 48 50 51 52 54 56 57 58
 59 60 62 63 64 65 66 67 69 70 73 74]
test_index [ 2  6  9 10 17 33 40 47 49 53 55 61 68 71 72]
train_index [ 2  3  4  5  6  7  9 10 12 13 14 15 16 17 18 19 21 24 25 27 29 31 32 33
 34 35 36 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 55 57 58 59 60
 61 62 63 64 65 66 67 68 69 70 71 72]
test_index [ 0  1  8 11 20 22 23 26 28 30 37 54 56 73 74]
train_index [ 0  1  2  5  6  7  8  9 10 11 13 14 15 17 19 20 21 22 23 24 26 28 30 31
 32 33 35 36 37 40 41 42 43 44 46 47 48 49 50 51 53 54 55 56 57 58 59 60
 61 62 63 64 65 67 68 70 71 72 73 74]
test_index [ 3  4 12 16 18 25 27 29 34 38 39 45 52 66 69]
train_index [ 0  1  2  3  4  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
 25 26 27 28 29 30 31 33 34 35 37 38 39 40 44 45 47 49 50 52 53 54 55 56
 57 61 62 64 65 66 68 69 71 72 73 74]
test_index [ 5 32 36 41 42 43 46 48 51 58 59 60 63 67 70]
train_index [ 0  1  2  3  4  5  6  8  9 10 11 12 16 17 18 20 22 23 25 26 27 28 29 30
 32 33 34 36 37 38 39 40 41 42 43 45 46 47 48 49 51 52 53 54 55 56 58 59
 60 61 63 66 67 68 69 70 71 72 73 74]
test_index [ 7 13 14 15 19 21 24 31 35 44 50 57 62 64 65]
train_index [ 0  1  2  3  4  6  7  8  9 10 11 12 13 15 16 17 18 19 22 23 24 26 27 28
 30 31 32 33 34 35 36 37 38 39 43 44 45 46 47 48 51 52 53 54 55 56 57 59
 60 61 62 65 66 67 68 69 70 72 73 74]
test_index [ 5 14 20 21 25 29 40 41 42 49 50 58 63 64 71]
train_index [ 0  1  2  3  4  5  7  9 11 14 15 18 19 20 21 22 23 25 26 27 28 29 30 31
 32 33 34 35 36 37 38 39 40 41 42 44 46 47 48 49 50 51 52 53 55 56 57 58
 60 61 62 63 64 65 67 68 69 70 71 72]
test_index [ 6  8 10 12 13 16 17 24 43 45 54 59 66 73 74]
train_index [ 0  1  3  4  5  6  8  9 10 12 13 14 15 16 17 18 20 21 22 23 24 25 28 29
 30 31 32 33 35 38 40 41 42 43 44 45 46 47 48 49 50 51 53 54 56 57 58 59
 60 61 62 63 64 66 68 69 71 72 73 74]
test_index [ 2  7 11 19 26 27 34 36 37 39 52 55 65 67 70]
train_index [ 2  4  5  6  7  8  9 10 11 12 13 14 15 16 17 19 20 21 22 24 25 26 27 28
 29 32 34 36 37 38 39 40 41 42 43 45 46 47 49 50 52 53 54 55 56 57 58 59
 61 63 64 65 66 67 68 70 71 72 73 74]
test_index [ 0  1  3 18 23 30 31 33 35 44 48 51 60 62 69]
train_index [ 0  1  2  3  5  6  7  8 10 11 12 13 14 16 17 18 19 20 21 23 24 25 26 27
 29 30 31 33 34 35 36 37 39 40 41 42 43 44 45 48 49 50 51 52 54 55 58 59
 60 62 63 64 65 66 67 69 70 71 73 74]
test_index [ 4  9 15 22 28 32 38 46 47 53 56 57 61 68 72]
train_index [ 2  3  4  6  8  9 10 11 12 13 14 15 16 18 19 20 21 22 23 24 26 27 29 30
 32 33 34 35 36 37 38 39 40 42 44 45 46 47 48 49 50 51 53 54 56 59 60 61
 62 63 64 65 66 67 68 70 71 72 73 74]
test_index [ 0  1  5  7 17 25 28 31 41 43 52 55 57 58 69]
train_index [ 0  1  3  4  5  6  7  8 11 12 13 15 16 17 18 19 20 21 22 23 24 25 27 28
 29 30 31 32 34 35 36 40 41 43 44 45 47 48 50 52 53 54 55 56 57 58 59 60
 61 63 64 65 67 68 69 70 71 72 73 74]
test_index [ 2  9 10 14 26 33 37 38 39 42 46 49 51 62 66]
train_index [ 0  1  2  5  7  9 10 11 12 14 16 17 18 19 21 22 23 24 25 26 28 29 31 33
 34 35 36 37 38 39 40 41 42 43 46 47 48 49 50 51 52 54 55 56 57 58 59 61
 62 63 65 66 67 68 69 70 71 72 73 74]
test_index [ 3  4  6  8 13 15 20 27 30 32 44 45 53 60 64]
train_index [ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 17 20 22 23 24 25 26 27
 28 30 31 32 33 34 35 36 37 38 39 41 42 43 44 45 46 48 49 51 52 53 54 55
 57 58 60 61 62 63 64 66 68 69 72 73]
test_index [16 18 19 21 29 40 47 50 56 59 65 67 70 71 74]
train_index [ 0  1  2  3  4  5  6  7  8  9 10 13 14 15 16 17 18 19 20 21 25 26 27 28
 29 30 31 32 33 37 38 39 40 41 42 43 44 45 46 47 49 50 51 52 53 55 56 57
 58 59 60 62 64 65 66 67 69 70 71 74]
test_index [11 12 22 23 24 34 35 36 48 54 61 63 68 72 73]
train_index [ 0  2  3  4  5  7  8  9 10 12 13 14 15 16 17 18 19 20 22 24 25 26 27 28
 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 46 47 48 49 51 52 53 57 58
 59 60 61 62 63 64 65 66 67 69 73 74]
test_index [ 1  6 11 21 23 29 45 50 54 55 56 68 70 71 72]
train_index [ 0  1  2  3  4  5  6  7  9 10 11 12 15 16 18 19 20 21 23 24 25 26 27 28
 29 30 31 32 34 35 36 37 38 39 40 43 44 45 46 48 49 50 51 52 53 54 55 56
 57 59 60 63 64 65 66 68 69 70 71 72]
test_index [ 8 13 14 17 22 33 41 42 47 58 61 62 67 73 74]
train_index [ 1  2  3  4  5  6  7  8  9 11 12 13 14 16 17 18 19 21 22 23 25 26 27 28
 29 30 33 35 36 37 38 41 42 43 44 45 47 48 50 53 54 55 56 57 58 59 60 61
 62 64 65 66 67 68 69 70 71 72 73 74]
test_index [ 0 10 15 20 24 31 32 34 39 40 46 49 51 52 63]
train_index [ 0  1  3  4  5  6  7  8 10 11 13 14 15 16 17 18 20 21 22 23 24 28 29 30
 31 32 33 34 35 36 37 39 40 41 42 44 45 46 47 49 50 51 52 54 55 56 58 59
 61 62 63 64 65 67 68 70 71 72 73 74]
test_index [ 2  9 12 19 25 26 27 38 43 48 53 57 60 66 69]
train_index [ 0  1  2  6  8  9 10 11 12 13 14 15 17 19 20 21 22 23 24 25 26 27 29 31
 32 33 34 38 39 40 41 42 43 45 46 47 48 49 50 51 52 53 54 55 56 57 58 60
 61 62 63 66 67 68 69 70 71 72 73 74]
test_index [ 3  4  5  7 16 18 28 30 35 36 37 44 59 64 65]
train_index [ 0  1  2  4  5  9 10 12 15 16 17 18 19 20 21 22 24 25 26 27 28 29 30 31
 32 33 34 36 38 39 40 41 42 44 45 46 47 48 49 50 51 52 54 55 56 57 58 59
 60 61 62 63 64 65 66 68 69 71 72 73]
test_index [ 3  6  7  8 11 13 14 23 35 37 43 53 67 70 74]
train_index [ 0  1  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 20 21 22 23 24 25 26
 27 28 29 31 32 33 34 35 37 40 42 43 44 45 46 47 49 50 53 54 55 56 57 58
 59 60 61 62 63 65 67 68 69 70 72 74]
test_index [ 2 18 19 30 36 38 39 41 48 51 52 64 66 71 73]
train_index [ 0  1  2  3  4  5  6  7  8  9 11 12 13 14 16 17 18 19 23 24 26 27 28 29
 30 32 34 35 36 37 38 39 40 41 43 44 45 46 48 49 50 51 52 53 56 57 58 59
 60 62 63 64 65 66 67 70 71 72 73 74]
test_index [10 15 20 21 22 25 31 33 42 47 54 55 61 68 69]
train_index [ 2  3  6  7  8 10 11 12 13 14 15 16 18 19 20 21 22 23 25 26 27 28 30 31
 32 33 34 35 36 37 38 39 40 41 42 43 45 47 48 49 51 52 53 54 55 57 59 60
 61 62 63 64 66 67 68 69 70 71 73 74]
test_index [ 0  1  4  5  9 17 24 29 44 46 50 56 58 65 72]
train_index [ 0  1  2  3  4  5  6  7  8  9 10 11 13 14 15 17 18 19 20 21 22 23 24 25
 29 30 31 33 35 36 37 38 39 41 42 43 44 46 47 48 50 51 52 53 54 55 56 58
 61 64 65 66 67 68 69 70 71 72 73 74]
test_index [12 16 26 27 28 32 34 40 45 49 57 59 60 62 63]

from sklearn.model_selection import cross_validate
cross_validate(knn,X_train,y_train,cv=rkf,scoring="accuracy",return_estimator=True)

{'fit_time': array([0.00099969, 0.        , 0.00099897, 0.        , 0.        ,
        0.00100088, 0.00100112, 0.        , 0.        , 0.        ,
        0.        , 0.        , 0.00099134, 0.00101256, 0.00099635,
        0.        , 0.        , 0.        , 0.00099874, 0.        ,
        0.00105643, 0.        , 0.        , 0.        , 0.        ,
        0.        , 0.        , 0.        , 0.        , 0.        ,
        0.        , 0.        , 0.        , 0.        , 0.00100422,
        0.        , 0.        , 0.        , 0.        , 0.        ,
        0.        , 0.        , 0.        , 0.        , 0.        ,
        0.        , 0.        , 0.        , 0.        , 0.        ]),
 'score_time': array([0.00099945, 0.00100017, 0.        , 0.00099826, 0.0010016 ,
        0.00099826, 0.00112462, 0.00212598, 0.00103188, 0.00099683,
        0.0009737 , 0.00103641, 0.        , 0.        , 0.        ,
        0.00097394, 0.00102925, 0.00099778, 0.        , 0.00100136,
        0.        , 0.        , 0.        , 0.        , 0.        ,
        0.00100565, 0.00099897, 0.        , 0.00099373, 0.00099897,
        0.00100088, 0.00106072, 0.00103712, 0.00107408, 0.        ,
        0.        , 0.        , 0.        , 0.        , 0.        ,
        0.        , 0.        , 0.        , 0.        , 0.        ,
        0.        , 0.00101113, 0.0010767 , 0.00099373, 0.00093102]),
 'estimator': [KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6),
  KNeighborsClassifier(n_neighbors=6)],
 'test_score': array([1.        , 1.        , 1.        , 1.        , 0.93333333,
        1.        , 1.        , 1.        , 1.        , 1.        ,
        1.        , 1.        , 1.        , 1.        , 1.        ,
        1.        , 1.        , 1.        , 1.        , 1.        ,
        0.93333333, 1.        , 1.        , 1.        , 1.        ,
        1.        , 1.        , 1.        , 1.        , 1.        ,
        1.        , 1.        , 1.        , 1.        , 1.        ,
        1.        , 1.        , 1.        , 1.        , 1.        ,
        1.        , 1.        , 1.        , 1.        , 1.        ,
        1.        , 1.        , 1.        , 1.        , 1.        ])}

#5 搜索一下什么样的邻居个数K是最好的，K的范围这里设置为1,10
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_validate
def getBestK(X_train,y_train,K):
    best_score=0
    best_k=1
#     X_train_set,X_val,y_train_set,y_val=train_test_split(X_train,y_train)
    rkf=RepeatedKFold(n_repeats=5,n_splits=5,random_state=42)
    for num in range(1,K):
        knn=KNeighborsClassifier(num)
        result=cross_validate(knn,X_train,y_train,cv=rkf,scoring="f1")
        score=result["test_score"].mean()
        score=round(score,2)
        print(score,num)
        if score>best_score:
            best_k=num
            best_score=score
    return best_k,best_score

best_k,best_score=getBestK(X_train,y_train,15)
best_k,best_score

knn=KNeighborsClassifier(best_k)
knn.fit(X_train,y_train)
knn.score(X_test,y_test)

1.0

自动调参吧，试试循环，找到最优的k值

实验1 试试用KNN完成回归任务

1 准备数据

import numpy as np
x1=np.linspace(-10,10,100)
x2=np.linspace(-5,15,100)

#手动构造一些数据
w1=5
w2=4
y=x1*w1+x2*w2
y

array([-70.        , -68.18181818, -66.36363636, -64.54545455,
       -62.72727273, -60.90909091, -59.09090909, -57.27272727,
       -55.45454545, -53.63636364, -51.81818182, -50.        ,
       -48.18181818, -46.36363636, -44.54545455, -42.72727273,
       -40.90909091, -39.09090909, -37.27272727, -35.45454545,
       -33.63636364, -31.81818182, -30.        , -28.18181818,
       -26.36363636, -24.54545455, -22.72727273, -20.90909091,
       -19.09090909, -17.27272727, -15.45454545, -13.63636364,
       -11.81818182, -10.        ,  -8.18181818,  -6.36363636,
        -4.54545455,  -2.72727273,  -0.90909091,   0.90909091,
         2.72727273,   4.54545455,   6.36363636,   8.18181818,
        10.        ,  11.81818182,  13.63636364,  15.45454545,
        17.27272727,  19.09090909,  20.90909091,  22.72727273,
        24.54545455,  26.36363636,  28.18181818,  30.        ,
        31.81818182,  33.63636364,  35.45454545,  37.27272727,
        39.09090909,  40.90909091,  42.72727273,  44.54545455,
        46.36363636,  48.18181818,  50.        ,  51.81818182,
        53.63636364,  55.45454545,  57.27272727,  59.09090909,
        60.90909091,  62.72727273,  64.54545455,  66.36363636,
        68.18181818,  70.        ,  71.81818182,  73.63636364,
        75.45454545,  77.27272727,  79.09090909,  80.90909091,
        82.72727273,  84.54545455,  86.36363636,  88.18181818,
        90.        ,  91.81818182,  93.63636364,  95.45454545,
        97.27272727,  99.09090909, 100.90909091, 102.72727273,
       104.54545455, 106.36363636, 108.18181818, 110.        ])

x1=x1.reshape(len(x1),1)
x2=x2.reshape(len(x2),1)
y=y.reshape(len(y),1)

import pandas as pd
data=np.hstack([x1,x2,y])

# 给数据加点噪声
np.random.seed=10
data=data+np.random.normal(0.1,1,[100,3])
data

array([[-9.80997918e+00, -4.47671228e+00, -6.86113562e+01],
       [-9.07863100e+00, -3.29030887e+00, -6.75412089e+01],
       [-8.17535392e+00, -4.85515660e+00, -6.56682184e+01],
       [-9.33603110e+00, -4.67304042e+00, -6.39943055e+01],
       [-8.31454149e+00, -3.61401814e+00, -6.15552168e+01],
       [-9.35462761e+00, -3.99216837e+00, -6.16450829e+01],
       [-7.35641032e+00, -5.10713257e+00, -5.80574405e+01],
       [-7.75808720e+00, -2.81374154e+00, -5.72785817e+01],
       [-7.85420726e+00, -3.25192460e+00, -5.58260703e+01],
       [-7.79785201e+00, -4.59268755e+00, -5.46208629e+01],
       [-9.90411101e+00, -7.55985286e-01, -5.19239440e+01],
       [-4.91167456e+00, -1.48242138e+00, -5.06778041e+01],
       [-9.25608953e+00, -1.12391146e+00, -4.80701720e+01],
       [-6.92987717e+00, -3.58106474e+00, -4.58459514e+01],
       [-7.19890084e+00, -2.10260074e+00, -4.46497119e+01],
       [-8.56812108e+00, -2.45314063e+00, -4.19130070e+01],
       [-6.97527315e+00, -3.25615055e+00, -4.15373469e+01],
       [-6.09201512e+00, -1.07060626e+00, -4.05034362e+01],
       [-5.94248008e+00,  6.42232477e-01, -3.64281226e+01],
       [-5.99567467e+00, -2.26531046e+00, -3.32873129e+01],
       [-7.56906953e+00, -6.81005515e-01, -3.42368449e+01],
       [-6.54272630e+00, -7.32829423e-01, -3.18556358e+01],
       [-4.68241322e+00, -1.55653397e+00, -2.99105801e+01],
       [-5.61148642e+00, -1.96269845e+00, -2.80144819e+01],
       [-4.64818297e+00,  2.21684956e-01, -2.56420739e+01],
       [-5.64237828e+00, -5.05215614e-02, -2.44150985e+01],
       [-4.77269716e+00,  3.12543954e-01, -2.35962190e+01],
       [-3.93579614e+00,  3.14368041e-01, -2.04078436e+01],
       [-4.67599369e+00,  1.38646098e+00, -1.95569688e+01],
       [-4.56613680e+00,  2.18761537e-01, -1.76443732e+01],
       [-4.12462083e+00,  7.81731566e-01, -1.55500903e+01],
       [-5.00893448e+00,  8.43167883e-01, -1.37904298e+01],
       [-3.32575389e+00,  8.87284515e-01, -1.16870554e+01],
       [-4.60962500e+00,  2.47674165e+00, -9.43497025e+00],
       [-2.55399230e+00,  1.60304976e+00, -7.30116575e+00],
       [-3.92552974e+00,  2.02861216e+00, -8.47211685e+00],
       [-2.85445054e+00,  1.32252697e+00, -2.27221086e+00],
       [-3.20383909e+00,  1.56885433e+00, -1.46024067e+00],
       [-1.87732669e+00,  1.18972183e+00, -1.68276177e+00],
       [-1.35842429e+00,  3.76086938e+00,  3.35135047e-01],
       [-7.24957523e-01,  4.37716480e+00,  1.17352349e+00],
       [-3.70453016e+00,  5.08438460e+00,  3.35207490e+00],
       [-7.97872551e-01,  2.78241431e+00,  5.09073378e+00],
       [-3.08232423e+00,  4.21925884e+00,  7.90719675e+00],
       [ 5.28844300e-01,  4.16412164e+00,  1.01885052e+01],
       [-2.64895900e-02,  4.04451188e+00,  1.32964325e+01],
       [ 7.67644414e-01,  4.38295411e+00,  1.20330676e+01],
       [-3.17298624e-01,  5.52193479e+00,  1.44587349e+01],
       [-4.05576007e-01,  6.15916945e+00,  1.77192591e+01],
       [ 2.58635850e-01,  4.36652636e+00,  2.08469868e+01],
       [-1.15875757e+00,  5.86049204e+00,  2.12312972e+01],
       [-7.16862753e-01,  7.60609045e+00,  2.24464377e+01],
       [ 1.00827677e+00,  7.13593566e+00,  2.60236434e+01],
       [ 8.64304920e-01,  7.70071685e+00,  2.67335947e+01],
       [ 3.14401551e+00,  5.74841619e+00,  2.76627520e+01],
       [-1.18085370e-02,  5.45967297e+00,  3.01731518e+01],
       [ 9.67211352e-01,  6.30044676e+00,  3.31847137e+01],
       [ 1.32254229e+00,  6.51216091e+00,  3.31636096e+01],
       [ 9.66206984e-01,  8.15352634e+00,  3.54552668e+01],
       [ 1.50374715e+00,  8.38063421e+00,  3.82675089e+01],
       [ 1.20333031e+00,  8.30155252e+00,  4.05759780e+01],
       [ 2.84702572e+00,  7.44997601e+00,  4.16313092e+01],
       [ 2.82319554e+00,  7.03396275e+00,  4.33733979e+01],
       [ 3.88755763e+00,  9.63373825e+00,  4.63550733e+01],
       [ 3.31979805e+00,  1.00825563e+01,  4.66602506e+01],
       [ 3.67714879e+00,  8.98817386e+00,  4.71815191e+01],
       [ 5.61673924e+00,  8.83321195e+00,  4.90218726e+01],
       [ 4.64376606e+00,  1.05003123e+01,  5.16821640e+01],
       [ 3.38312917e+00,  9.93985678e+00,  5.44523927e+01],
       [ 2.90435391e+00,  8.76211593e+00,  5.72974806e+01],
       [ 1.94362594e+00,  8.37086325e+00,  5.69748221e+01],
       [ 4.86357671e+00,  8.79920772e+00,  5.92178403e+01],
       [ 5.21731274e+00,  8.76064972e+00,  6.30249467e+01],
       [ 5.86040809e+00,  1.12868041e+01,  6.26973140e+01],
       [ 4.05985223e+00,  8.65847315e+00,  6.61012727e+01],
       [ 6.19899121e+00,  8.30649111e+00,  6.37680817e+01],
       [ 5.73989925e+00,  1.00161474e+01,  6.92336558e+01],
       [ 5.38266361e+00,  1.03971821e+01,  7.17084241e+01],
       [ 7.23264561e+00,  1.20494918e+01,  7.05362027e+01],
       [ 6.11948179e+00,  1.19855375e+01,  7.55318286e+01],
       [ 8.03847795e+00,  9.79749582e+00,  7.47950707e+01],
       [ 8.30070319e+00,  1.07233637e+01,  7.93806649e+01],
       [ 7.44456666e+00,  1.11936713e+01,  7.84042566e+01],
       [ 6.87035796e+00,  1.23168763e+01,  8.01532295e+01],
       [ 6.57153443e+00,  1.12686434e+01,  8.32735790e+01],
       [ 8.06216701e+00,  1.26805930e+01,  8.58973008e+01],
       [ 8.75001919e+00,  1.36698902e+01,  8.72099703e+01],
       [ 7.30252179e+00,  1.34260600e+01,  8.71816534e+01],
       [ 1.02174549e+01,  1.12734356e+01,  9.06574864e+01],
       [ 9.16397441e+00,  1.35946035e+01,  9.12502949e+01],
       [ 7.65119402e+00,  1.26062408e+01,  9.37067133e+01],
       [ 7.88012441e+00,  1.20190767e+01,  9.49682650e+01],
       [ 8.32044954e+00,  1.32807945e+01,  9.65808990e+01],
       [ 8.01089317e+00,  1.64722621e+01,  9.82354518e+01],
       [ 9.02271142e+00,  1.33190747e+01,  1.00825525e+02],
       [ 8.09970303e+00,  1.46680917e+01,  1.03017581e+02],
       [ 1.13875348e+01,  1.46989516e+01,  1.04003935e+02],
       [ 1.01333057e+01,  1.33257429e+01,  1.05931984e+02],
       [ 9.38629399e+00,  1.39040038e+01,  1.10363757e+02],
       [ 1.13412247e+01,  1.61090392e+01,  1.10731822e+02]])

#将数据拆分成训练数据和测试数据
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test=train_test_split(data[:,:2],data[:,-1])
X_train.shape,X_test.shape,y_train.shape,y_test.shape

((75, 2), (25, 2), (75,), (25,))

2 通过K个近邻预测的标签的距离来预测当前样本的标签

#改写函数
#返回所有近邻的标签的均值作为当前x的预测值
def calcu_distance_return(x,X_train,y_train):
    KNN_x=[]
    #遍历训练集中的每个样本
    for i in range(X_train.shape[0]):
        if len(KNN_x)<K:
            KNN_x.append((euclidean(x,X_train[i]),y_train[i]))
        else:
            KNN_x.sort()
            for j in range(K): 
                if (euclidean(x,X_train[i]))< KNN_x[j][0]:
                    KNN_x[j]=(euclidean(x,X_train[i]),y_train[i])
                    break
    knn_label=[item[1] for item in KNN_x]           
    return np.mean(knn_label)

#对整个测试集进行预测
def predict(X_test):
    y_pred=np.zeros(X_test.shape[0])
    for i in range(X_test.shape[0]):
        y_hat_i=calcu_distance_return(X_test[i],X_train,y_train) 
        y_pred[i]=y_hat_i
    return y_pred

#输出预测结果
y_pred= predict(X_test)
y_pred

array([-48.77391118, -61.82953142,  -7.08681066,  31.79119171,
        89.89605669,  49.28413251,  52.97713079,  33.48545677,
        63.32131747,  98.05154212, -55.78008004,  98.04210317,
         7.02443886, -19.02562562,  11.49285143, -13.67585848,
        52.97713079,  21.82629113,  10.45687568,  55.14568247,
        -9.552268  ,  94.91846026, -11.51277047,  22.35944142,
        86.13169115])

y_test

array([-41.53734685, -58.05744051,  -1.46024067,  40.57597798,
       103.01758072,  66.10127272,  46.66025056,  56.97482206,
        63.0249467 , 100.8255246 , -54.62086294,  91.25029492,
         3.3520749 , -23.59621905,   1.17352349, -20.40784363,
        46.35507328,  21.23129715,   5.09073378,  59.21784029,
         7.90719675,  98.23545178,  -1.68276177,  17.71925914,
        78.40425661])

3 通过R方进行评估

from sklearn.metrics import r2_score
r2_score(y_test,y_pred)

0.9634297760055799

	sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)	target
0	5.1	3.5	1.4	0.2	0
1	4.9	3.0	1.4	0.2	0
2	4.7	3.2	1.3	0.2	0
3	4.6	3.1	1.5	0.2	0
4	5.0	3.6	1.4	0.2	0
...	...	...	...	...	...
145	6.7	3.0	5.2	2.3	2
146	6.3	2.5	5.0	1.9	2
147	6.5	3.0	5.2	2.0	2
148	6.2	3.4	5.4	2.3	2
149	5.9	3.0	5.1	1.8	2

	sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)
0	5.1	3.5	1.4	0.2
1	4.9	3.0	1.4	0.2
2	4.7	3.2	1.3	0.2
3	4.6	3.1	1.5	0.2
4	5.0	3.6	1.4	0.2

	sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)	target
0	5.1	3.5	1.4	0.2	0
1	4.9	3.0	1.4	0.2	0
2	4.7	3.2	1.3	0.2	0
3	4.6	3.1	1.5	0.2	0
4	5.0	3.6	1.4	0.2	0
...	...	...	...	...	...
145	6.7	3.0	5.2	2.3	2
146	6.3	2.5	5.0	1.9	2
147	6.5	3.0	5.2	2.0	2
148	6.2	3.4	5.4	2.3	2
149	5.9	3.0	5.1	1.8	2

	sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)
0	5.1	3.5	1.4	0.2
1	4.9	3.0	1.4	0.2
2	4.7	3.2	1.3	0.2
3	4.6	3.1	1.5	0.2
4	5.0	3.6	1.4	0.2

【Python机器学习】实验06 KNN最近邻算法

文章目录

KNN算法

前言 距离度量

(1) 欧式距离

(2) 曼哈顿距离(Manhattan distance)

(3) 切比雪夫距离(Chebyshev distance)

(4) 闵可夫斯基距离(Minkowski distance)

(5) 汉明距离(Hamming distance)

(6) 余弦相似度(Cosine Similarity)

KNN算法介绍

1 数据的准备

2 划分训练数据和测试数据

3 通过K个近邻预测的标签的距离来预测当前样本的标签

4 计算准确率

试试Scikit-learn

sklearn.neighbors.KNeighborsClassifier

实验1 试试用KNN完成回归任务

1 准备数据

2 通过K个近邻预测的标签的距离来预测当前样本的标签

3 通过R方进行评估

相关文章

前言距离度量

	sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)	target
0	5.1	3.5	1.4	0.2	0
1	4.9	3.0	1.4	0.2	0
2	4.7	3.2	1.3	0.2	0
3	4.6	3.1	1.5	0.2	0
4	5.0	3.6	1.4	0.2	0
...	...	...	...	...	...
145	6.7	3.0	5.2	2.3	2
146	6.3	2.5	5.0	1.9	2
147	6.5	3.0	5.2	2.0	2
148	6.2	3.4	5.4	2.3	2
149	5.9	3.0	5.1	1.8	2

	sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)
0	5.1	3.5	1.4	0.2
1	4.9	3.0	1.4	0.2
2	4.7	3.2	1.3	0.2
3	4.6	3.1	1.5	0.2
4	5.0	3.6	1.4	0.2