倍增与ST算法
- 倍增
- 倍增原理
- 倍增法的局限
- 例题 :国旗计划 (洛谷 P4155)
- 例题题解
- 带注释的代码
- ST算法
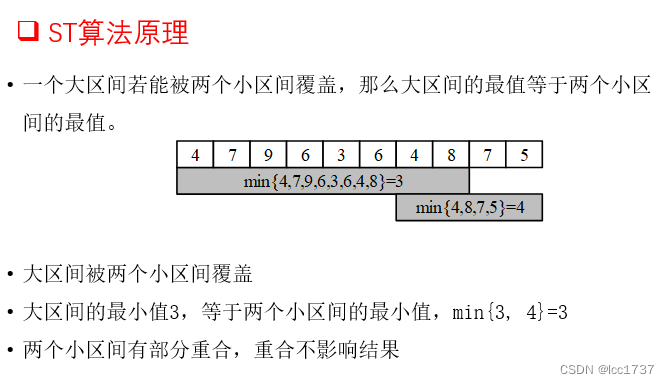
- ST算法原理
- ST算法步骤
- ST算法应用场合
- 例题 :【模板】ST表 (洛谷 P3865)
倍增
倍增原理


倍增法的局限

例题 :国旗计划 (洛谷 P4155)

例题题解
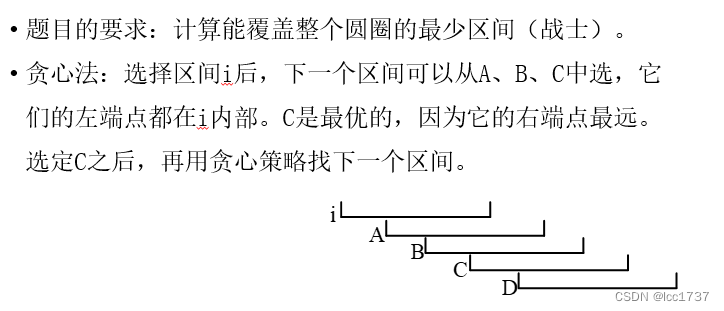
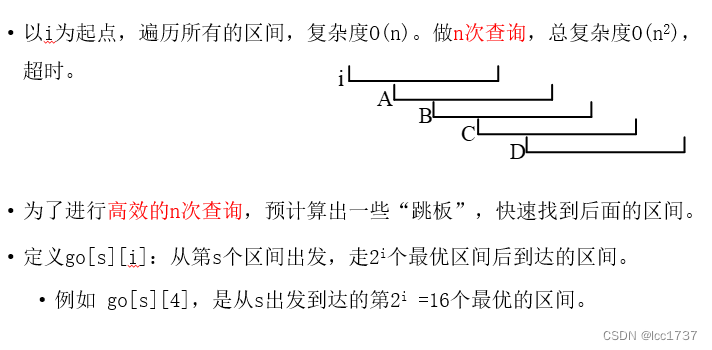
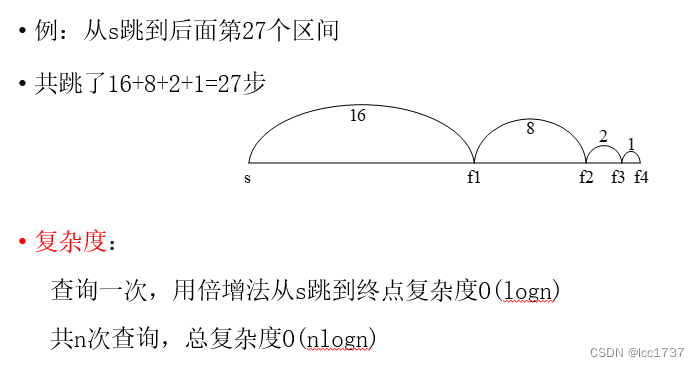
带注释的代码
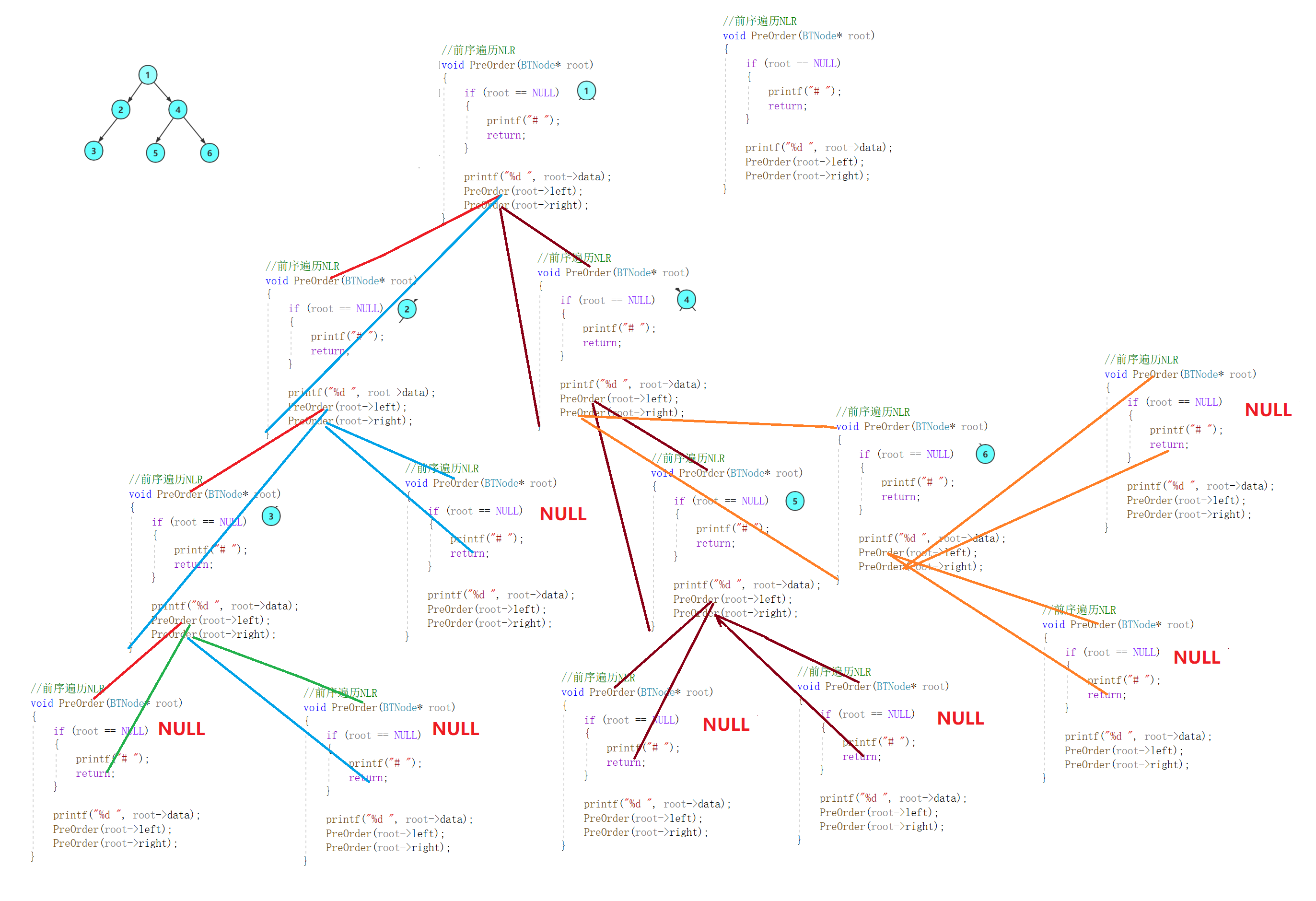
/*
只需要知道
go[i, 0] = i 往后跳 2^0 = 1次
可以求
go[i, k] = i 往后跳 2^k 次
求的过程:
go[i, k] = go[go[i, k - 1], k - 1]
按照k 从小到大求
题目
我s区间, 求最少多少次跳跃最优区间可以覆盖所有的点
假如跳x次最优区间之后, 它的右端点第一次>=l[s]
那么我的答案就是x
l[s]------>m ---->(>=l[s])
ne[i, 2] = i 往后跳 2^2 次
ne[i - 1, 0] = i
ne[i - 1, 1] = i - 1 + 1 + 2
ne[ne[i - 1, 0], 0]
int s;
int startl = l[s]
最终答案x
x = (1010110)_2
2^6 √
对于我现在的s
x = (0010110)
2^5 x
2^4 √
2^2 √
x = (0000010)
2^1 x
2^0 √
x = (0000001)
for (int i = 18; i >= 0; i -- ) {
if(r[go[s][i]] < startl) {
s = go[s][i];
}
}
r[s] < startl
r[go[s][0]] >= startl
思路:
1.分析贪心策略
2.考虑倍增, 预处理go[s, k]
1. 处理go[s, 0]
2. 通过go[s, i]->go[s, i + 1]
3. 二进制求值
for (int i = 18; i >= 0; i -- ) {
if(r[go[s][i]] < startl) {
s = go[s][i];
}
}
1 : [1, 5]
2 : [2, 4]
3 : [3, 6]
(1, 2) 不合法的
(1, 3), (2, 3) 合法的
l[i] > l[j]
r[i] > r[j]
ST表
f[i][k] 代表着 [i, i+2^k-1] 区间的最小值
f[i][k] = min(f[i][k - 1], f[i + 2^(k-1)][k-1])
[i, i+2^k-1] = [i, i+2^{k-1}-1]U[i+2^{k-1}, i+2^k-1]
1.把f[i][0]求出来
2.递推求出f[i][k]
求[l, r]的最小值
query(l, r) :
int k = log2(r - l + 1)
return min(f[l, k], f[r - 2^k + 1, k]);
*/
#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 10;
int go[N][20];
// go[i][k] 代表第i个区间往后跳2^k次所在区间
int main() {
int n, m;
std::cin >> n >> m;
std::vector<array<int, 3>> seg(2 * n, {0, 0, 0});
// 输入数据, 将输入的环破坏了, 成为一个链
// 如果出现l > r的, 那么我们直接将 r += m
// 也就是说将[1, m] -> [1, 2 * m], [m + 1, 2 * m]部分也同样用于表示[1, m]
// 那么我如果是以s作为开始的区间, 那么我只要去寻找r >= l[s] + m的最小覆盖区间即可
for (int i = 0; i < n; i ++ ) {
int l, r;
std::cin >> l >> r;
seg[i] = {l, r, i};
if(l > r) {
seg[i][1] += m;
}
}
for (int i = n; i < 2 * n; i ++ ) {
seg[i] = seg[i - n];
seg[i][0] += m;
seg[i][1] += m;
}
// 给区间排序, 按照l, r, id从小到大排序
sort(seg.begin(), seg.end());
// 预处理第i个区间的最优区间
for (int i = 0, j = 0; i < 2 * n; i ++ ) {
// 找到最大的l[j] <= r[i]
while(j + 1 < 2 * n && seg[j + 1][0] <= seg[i][1]) {
j ++ ;
}
go[i][0] = j;
}
// 预处理go
for (int j = 1; j <= 19; j ++ ) {
for (int i = 0; i < 2 * n; i ++ ) {
go[i][j] = go[go[i][j - 1]][j - 1];
}
}
// 求答案
std::vector<int> ans(n);
for (int i = 0; i < n; i ++ ) {
int l = seg[i][0];
int r = seg[i][1];
int id = seg[i][2];
int s = i, bd = l + m; // 开始区间, 最终目标值
int ret = 1; //算是初始选的区间
for (int j = 19; j >= 0; j -- ) {
if(seg[go[s][j]][1] < bd) { // 如果没有超过目标
s = go[s][j]; // 跳跃
ret += (1 << j); // 算上答案
}
}
ret += 1; // 最后跳一次, 抵达目标
ans[id] = ret;
}
for (int i = 0; i < n; i ++ ) {
std::cout << ans[i] << " \n"[i == n - 1];
}
}
这个代码是使用了倍增法处理区间覆盖的问题。这种问题的关键在于找到覆盖目标区间需要的最少的跳跃次数。这个代码的基本思路是:
-
把环状的边防站变为线状,这样处理起来更方便。如果一个区间的左边界大于右边界,那么这个区间实际上是跨过了边界。我们把这个区间的右边界加上总的边防站数量,使其变为一个正常的区间。
-
根据区间的左边界和右边界进行排序,使得所有的区间按照左边界从小到大排列。
-
预处理每个区间的最优跳跃区间。具体来说,对于第i个区间,我们找到一个最大的j,使得第j个区间的左边界不超过第i个区间的右边界。这个j就是第i个区间的最优跳跃区间。
-
通过预处理的最优跳跃区间,我们可以快速地求出每个区间往后跳跃2^k次所在的区间。这样就大大减少了求解的时间复杂度。
-
对于每个起始区间,我们找到最少的跳跃次数,使得最后跳跃到的区间的右边界大于等于起始区间的左边界加上总的边防站数量。这个最少的跳跃次数就是我们要求的答案。
这个代码主要使用了贪心的策略,通过预处理的方式大大提高了效率。对于每个起始区间,我们总是尽可能地选择跳跃到最远的区间,直到覆盖了所有的目标点。
ST算法

ST算法原理
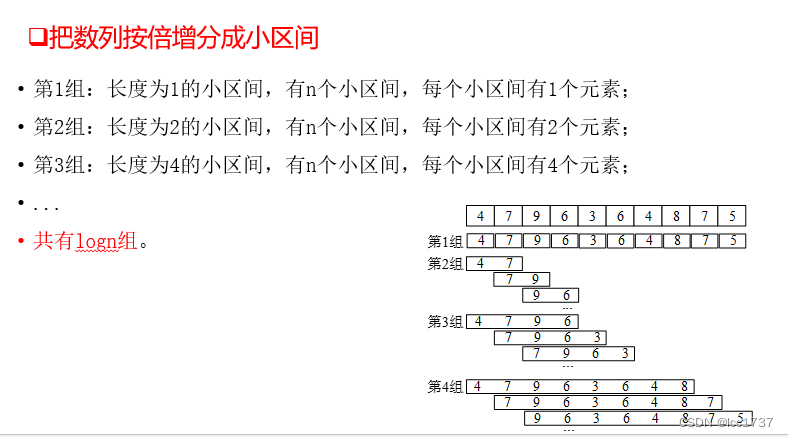
ST算法步骤


ST算法应用场合

例题 :【模板】ST表 (洛谷 P3865)
题目背景
这是一道 ST 表经典题——静态区间最大值
请注意最大数据时限只有 0.8s,数据强度不低,请务必保证你的每次查询复杂度为 O ( 1 ) O(1) O(1)。若使用更高时间复杂度算法不保证能通过。
如果您认为您的代码时间复杂度正确但是 TLE,可以尝试使用快速读入:
inline int read()
{
int x=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
return x*f;
}
函数返回值为读入的第一个整数。
快速读入作用仅为加快读入,并非强制使用。
题目描述
给定一个长度为 N N N 的数列,和 M M M 次询问,求出每一次询问的区间内数字的最大值。
输入格式
第一行包含两个整数 N , M N,M N,M,分别表示数列的长度和询问的个数。
第二行包含 N N N 个整数(记为 a i a_i ai),依次表示数列的第 i i i 项。
接下来 M M M 行,每行包含两个整数 l i , r i l_i,r_i li,ri,表示查询的区间为 [ l i , r i ] [l_i,r_i] [li,ri]。
输出格式
输出包含 M M M 行,每行一个整数,依次表示每一次询问的结果。
样例 #1
样例输入 #1
8 8
9 3 1 7 5 6 0 8
1 6
1 5
2 7
2 6
1 8
4 8
3 7
1 8
样例输出 #1
9
9
7
7
9
8
7
9
说明/提示
对于 30 % 30\% 30% 的数据,满足 1 ≤ N , M ≤ 10 1\le N,M\le 10 1≤N,M≤10。
对于 70 % 70\% 70% 的数据,满足 1 ≤ N , M ≤ 10 5 1\le N,M\le {10}^5 1≤N,M≤105。
对于 100 % 100\% 100% 的数据,满足 1 ≤ N ≤ 10 5 1\le N\le {10}^5 1≤N≤105, 1 ≤ M ≤ 2 × 10 6 1\le M\le 2\times{10}^6 1≤M≤2×106, a i ∈ [ 0 , 10 9 ] a_i\in[0,{10}^9] ai∈[0,109], 1 ≤ l i ≤ r i ≤ N 1\le l_i\le r_i\le N 1≤li≤ri≤N。
带注释的代码
#include <bits/stdc++.h>
using namespace std;
// 定义最大的序列长度 MAXN 和最大的 log 值 MAXLOG
const int MAXN = 100005, MAXLOG = 20;
// st[i][j] 存储的是从 i 开始,长度为 2^j 的区间的最大值
// Log[i] 存储的是 i 的二进制位数减 1,相当于 log2(i) 的下取整
// a[i] 用来存储输入的序列
int st[MAXN][MAXLOG], Log[MAXN];
int a[MAXN];
// 一个快速读入的函数,用于提高读入效率
inline int read() {
int x=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
return x*f;
}
// 查询函数,接受查询区间的两个边界,返回区间内的最大值
int query(int l, int r) {
int k = Log[r - l + 1]; // 计算区间长度的 log 值
// 返回两个重叠的区间的最大值,这两个区间都是最大的可以包含在查询区间内的2的幂长度的区间
return max(st[l][k], st[r - (1 << k) + 1][k]);
}
int main() {
// 读取数列的长度 N 和查询的次数 M
int N = read(), M = read();
// 初始化 Log 数组,预处理出 1 到 N 的每个数的 log 值
Log[1] = 0;
for(int i = 2; i <= N; i++)
Log[i] = Log[i / 2] + 1;
// 读取数列并构造 ST 表
// st[i][0] 是数列的原始数据
for(int i = 1; i <= N; i++)
st[i][0] = read();
// 构造 ST 表,计算出从每个位置开始的,长度为 2 的幂的每个区间的最大值
for(int j = 1; j <= 20; j++)
for(int i = 1; i + (1 << j) - 1 <= N; i++)
st[i][j] = max(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]);
// 进行 M 次查询,每次查询读取查询区间,然后通过 ST 表查询区间的最大值,并输出结果
while(M--) {
int l = read(), r = read();
printf("%d\n", query(l, r));
}
return 0;
}
这个代码主要是利用了 ST 表(Sparse Table,稀疏表)的性质来求区间最大值。它是一种预处理的方法,可以在 O(1) 的时间复杂度内查询到任意区间的最大值,非常适合解决这种区间查询的问题。