随着全球各行业的数据治理、数字化转型智能化辅助的引入发展,机器学习(包括深度学习)在逐步深入到各行各业,所以,有必要对机器学习的常见术语,经典算法及应用场景进行一次总结,其实机器学习兴起目的是为了解决人类的各种各样的分类回归问题,通过人类智能化的设计,实现机器的自动化或智能化,而且机器主要学习人类解决问题的归纳和综合逻辑方法,但目前还无法实现演绎逻辑。特别是一些数据量密集,准确性要求快捷及时的场景,比如人脸识别、车牌设备、行人检测、安全预警、垃圾邮件识别等等。
机器学习的几个关键名词:训练集、测试集、特征值、有监督、非监督、半监督、分类和回归。
训练集:用于训练算法形成模型的数据集组合,一般都是有标签的数据集。
测试集:用于测试训练形成的模型的测试验证数据集,一般与训练集的比例是2:8。
特征值:整个数据集中的所以特征数据,出去要预测的属性或属性值。
关于有监督、非监督、半监督、分类和回归在下面详细展开说明。
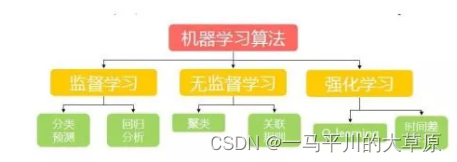
机器学习大的分类
分类问题:目标标记是类别型数据
回归问题:目标标记是连续性数值
机器学习三类问题
有监督学习:训练集有类别标记
无监督学习:无标记的训练集
半监督学习:有类别标记的训练集+无标记的训练集
深度学习:机器学习的延伸和扩展,强调的是特征提取与组合
强化学习:从环境到行为映射的学习,以使得奖励信号(强化信号)函数值最大,强调的是反馈
迁移学习:是在新情况(不同于训练集的情况)上的泛化能力。而把别处学得的知识,迁移到新场景的能力。人类的迁移学习能力就很强,
人类在学会骑自行车后,再骑摩托车就很容易了,人类在学会打羽毛球后再学习打网球也会容易很多。强调的是
适应能力,发现共性(最大的难点),共性:司机的座位总是靠近路中间的
迁移学习的特点:小规模数据,可靠性和个性化。
算法训练后形成的模型评估有哪些?
1.准确率或精度
2.速度
3.强壮性
4.可规模性
5.可解释性
深度学习和经典机器学习的区别
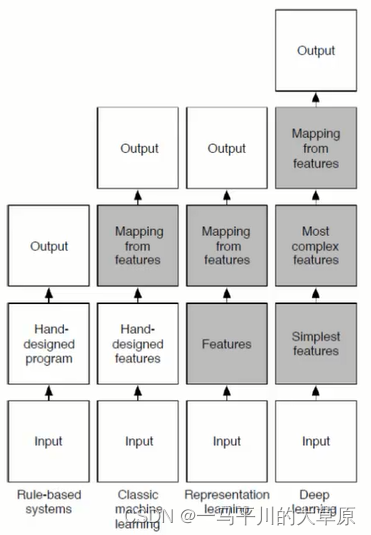
经典的机器学习算法如下:

一、决策树(DecisionTree)
信息熵:信息的不确定,衡量信息的多少,信息的不确定性越大,熵越大,建模时取信息增益最大的那个特征作为根节点(条件熵最小)
信息增益或信息获取量(Information Gain)或者互信息:特征属性获取的度量方法。Gain(A)=Info(D)-Info_A(D)
优点:便于理解,直观,对小规模数据集有效
缺点:处理连续变量不好,类别较多时,错误增加的比较快,可用规模性一般
scikit-learn,需要安装graphviz后执行以下命令,实现决策树图的可视化。
dot转化为pdf文件:dot -Tpdf test.dot -o output.pdf 生成决策树
二、最邻近规则分类算法(简称KNN)
基于实例的学习,懒惰学习,开始并没有建立广泛的模型
为了判断未知实例的类别,需要以所有已知类别的实例作为参考,对其进行归类
1.选择参数K
2.计算未知实例与所有已知实例之间的距离
3.选择最近K个已知实例
4.采用少数服从多数,未知实例的归类就是这K个相邻样本中最大数的类别
KD树构建:
分别计算n个特征取值的方差,用方差最大的第k维特征$n{k}$来作为根节点。对于这个特征,我们选择特征$n{k}$的取值的中位数$n{kv}$对应的样本作为划分点
距离衡量方法:坐标差平方和开根号,cos,相关度,曼哈顿距离
优点:简单易于理解,容易实现,可以通过对K的选择增加健壮性
缺点:空间大,算法复杂度高,当样本不平衡时,某一类样本占主导时,新的实例容易被归为这个主导分类。但实际是错误的
改进:在距离的基础上加一个权重,比如1/d(d为距离)
三、支持向量机(SVM)
机器学习的一般框架
训练集--》提取特征向量--》结合一定的算法(分类器:比如决策树,KNN)-->得到模型结果
SVM就是寻找两类的超平面,使得边际最大
特点:
1.算法复杂度是由支持向量的个数决定,不是由数据的维度决定,不容易产生overfitting
2.模型完全依赖于支持向量,即使所有非支持向量去除,重复训练时,模型也是一样的
3.一个SVM如果训练得出的支持向量个数比较少,模型容易被泛化
四、人工神经网络
多层向前神经网络(multiplayer feed-forward neural network)
输入层 隐藏层 输出层
交叉验证方法(cross-validation):分成十份,每次拿出一份,找到十个模型,然后去平均值
神经网络可以用于解决分类问题,也可以解决回归问题
backpropagation算法
1.通过迭代来处理训练集中的数据
2.通过对比神经网络后输入层预测值与真实值之间的差距
3.反方向(从输出--》隐藏--》输入)来最小化误差来更新每个连接的权重和偏向
终止条件
权重的更新低于某个阈值
预测的错误率低于某个阈值
达到预设一定的循环次数
五、简单线性回归(Simple linear regression)
均值、中位数,众数,方差和标准差(提醒数据的离散程度,越大表示离散度大)
回归Y变量是连续数值型:如房价、人数、
分类Y变量是类别型:颜色类型,岩石类型,电脑品牌,有无信誉
包含一个自变量和一个因变量叫做简单线性回归问题
包含两个以上的自变量,叫做多元回归问题。
简单线性回归模型:y=B0+B1x+E
简单线性回归方程:E(y)=B0+B1x
估计的简单线性回归方程:y=b0+b1x
估计方法:使得sum of squares最小


多元回归分析
多个自变量
非线性回归(logistic regression)
概率:一件事情发生的可能性衡量,0<P<1
条件概率
梯度下降算法
回归中的相关度和R平方值:皮尔逊相关系数

R平方值:决定系数,反应因变量的全部变异能通过回归关系被自变量解释的比例,比如R平方为0.8,表示回归关系可以解释因变量80%的变异,换句话说,如果我们能够控制自变量不变,泽因变量的变异程度会减少80%
R平方随着自变量的增加会变大,R平方和样本量有关系
 rer
rer
六、聚类(cluster)
Kmeans算法:数据挖掘中的十大经典算法之一
算法接收参数K,然后将事先输入的n个数据对象划分为k个聚类,同一聚类相似度高,不同聚类相似度变小
优点:速度快,简单
缺点:最终结果跟初始点的选择相关,容易陷入局部最优,需要事先知道K值
层次聚类(hierarchical clustering)
初始化将每个样本归为一类,计算每两类之间的距离,也就是样本与样本之间的相似度
寻找各个类之间最近的两个类,将其归为一类,相当于类的总数少一个了。
学习资源
深度学习的软件包:Theano,opencv2,Pylearn2,TensorFlow,scikit-neuralnetwork,Caffe(C++),Deeplearning4j(java),Torch
深度学习网站:http://deeplearning.net/
GPU查看网站:http://developer.nvidia.com/cuda-gpus
sklearn深度学习:GitHub - aigamedev/scikit-neuralnetwork: Deep neural networks without the learning cliff! Classifiers and regressors compatible with scikit-learn.
Mnist数据集(手写数据集):MNIST handwritten digit database, Yann LeCun, Corinna Cortes and Chris Burges, GitHub - cazala/mnist: mnist digits in javascript