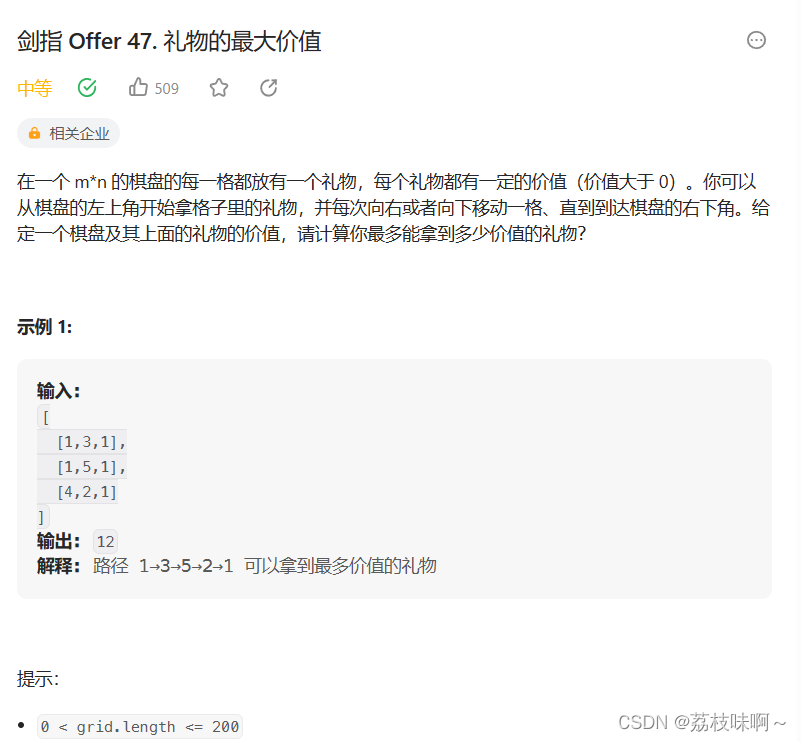
这道题挺简单，学过动态规划就会。如果要走到grid[i][j],那你的上一步必须是grid[i-1][j]或者grid[i][j-1],具体是grid[i-1][j]还是grid[i][j-1]，就看哪一步的价值最大，所以用一个与grid等大的dp数组来表示走到grid[i][j]的最大价值是dp[i][j]。最后返回dp数组的最后一个数就行。

首先初始话dp数组的第一行，第一行只能从左往右走，所以其实就是第一行累加到当前数就是dp[0][i]的值，接下来的数的动态转移方程是，如果dp[i-1]][j]>dp[i][j-1],dp[i][j]=dp[i-1][j]+grid[i][j],否则dp[i][j] = dp[i][j-1] + grid[i][j],当然这其中还要判断j-1是不是小于0，如果使得话说明这是一行第一个数他的左边没有数，只能从上面加。最后返回dp数组的最后一个数即可。以下是我的代码：

class Solution {
    public int maxValue(int[][] grid) {
      int row = grid.length;
      int clown = grid[0].length;
      int[][] dp = new int[row][clown];
      int sum =0;
      for(int i=0;i<clown;i++){
          sum+=grid[0][i];
          dp[0][i]=sum;
      }
      for(int i=1;i<row;i++){ 
          for(int j=0;j<clown;j++){
              if(j-1 >= 0){
                  if(dp[i-1][j] > dp[i][j-1]){
                      dp[i][j] = dp[i-1][j] + grid[i][j];
                  }else{
                      dp[i][j] = dp[i][j-1] + grid[i][j];
                  }
              }else{
                      dp[i][j] = dp[i-1][j] + grid[i][j];
              }
          }
      }
      return dp[row-1][clown-1];
    }
}

写完看了一下题解，题解稍微简洁一点，他的初始化是放在循环里一起完成，没有另外用一个循环。这是题解代码：

class Solution {
    public int maxValue(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        int[][] f = new int[m][n];
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (i > 0) {
                    f[i][j] = Math.max(f[i][j], f[i - 1][j]);
                }
                if (j > 0) {
                    f[i][j] = Math.max(f[i][j], f[i][j - 1]);
                }
                f[i][j] += grid[i][j];
            }
        }
        return f[m - 1][n - 1];
    }
}

第0行和第0列都是通过累加的方法完成的，其他位置的他用了两次比较，第一次比dp[i][j]和dp[i-1][j],第二次比dp[i][j]和dp[i-1][j]，取较大值，道理是一样的。