论文
Keyframe-Based Visual-Inertial SLAM Using Nonlinear Optimization
摘要
由于两种感知模式的互补性,视觉和惯性线索的融合在机器人中变得很流行。虽然迄今为止大多数融合策略都依赖于过滤方案,但视觉机器人界最近转向了非线性优化方法,用于视觉同步定位和映射(SLAM)等任务,因为他们发现这在性能质量和计算复杂性方面具有显著优势。根据这一趋势,我们提出了一种新的方法,将视觉测量与SLAM中惯性测量单元(IMU)的读数紧密集成。IMU误差项以完全概率的方式与界标重投影误差集成,导致要优化的联合非线性成本函数。利用“关键帧”这一强大的概念,我们部分边缘化了旧状态,以保持有限大小的优化窗口,确保实时操作。与纯视觉和松散耦合的视觉惯性算法相比,我们的实验证实了紧密融合在准确性和鲁棒性方面的优势。
INTRODUCTION
长期以来,将视觉和惯性测量相结合一直是解决机器人常见任务的流行方法,如自我运动估计、视觉里程计和SLAM。图像中捕捉到的场景的丰富表示,以及典型IMU中存在的陀螺仪和加速度计的准确短期估计,已被公认为是相辅相成的,在机载[6,20]和汽车[14]导航中有很大的用途。此外,随着这些传感器在大多数智能手机中的可用性,人们对视觉惯性SLAM的有效解决方案产生了极大的兴趣和研究活动。
从历史上看,视觉惯性姿态估计问题已经通过滤波来解决,其中IMU测量被传播,关键点测量被用来形成更新。Mourikis和Roumeliotis[14]提出了一种使用单目视觉的基于EKF的实时融合,而Jones和Soatto[8]提出了在长户外轨迹上的单目惯性滤波结果,包括IMU到相机的校准和闭环。这两项工作的表现都令人印象深刻,误差都低于行驶距离的0.5%。
Kelly和Sukhatme[9]提供了校准结果和基于滤波的视觉IMU融合背景下的可观测性研究。偏航和位置的全局不可观测性,以及相对于初始参考姿态的日益增长的不确定性,是视觉惯性估计问题的固有问题;这对通常依赖于某种形式的线性化的滤波方法提出了挑战。
在[18]中,表明在纯视觉SLAM中,与滤波方法相比,基于优化的方法为相同的计算工作提供了更好的精度。在非线性优化的情况下,保持关键帧及其相关地标的相对稀疏图一直很受欢迎
文献中发现的视觉惯性融合方法可以分为两种方法。在松耦合系统中,例如[10],IMU测量作为独立的倾角仪和相对偏航测量纳入立体视觉优化。Weiss等人[20]使用仅视觉姿态估计作为间接IMU传播的EKF的更新。同样在[15,7]中,相对立体姿态估计被集成到包含惯性项和绝对GPS测量的因子图中。这种方法限制了复杂性,但忽略了不同传感器内部状态之间的相关性。相反紧密耦合的方法联合估计所有传感器状态。
为了便于处理,并作为滤波的替代方案,Dong Si和Mourikis[2]提出了一种固定滞后平滑器,其中保持了连续机器人姿态和相关状态的窗口,从而边缘化了超出范围的状态(参见[19])。[16]中使用了类似的方法,但没有惯性项,并且在行星着陆的背景下使用。
为了实现稳健和准确的视觉惯性SLAM,我们提倡紧密耦合融合,尽可能最大限度地利用感知线索和非线性估计,而不是滤波,以减少线性化引起的次优性。我们的方法受到[17]的启发,其中提出在批量优化的SLAM中使用IMU误差项(尽管仅在初始化期间)。我们的方法与[2]中提出的固定滞后平滑器密切相关,因为它在单个成本函数中结合了惯性项和重投影误差,并且为了限制复杂性,旧状态被边缘化
三个贡献点
1) 当存在缓慢或根本没有运动时,我们也使用关键帧范式进行无漂移估计:我们不使用时间连续姿势的优化窗口,而是保留可能在时间上任意间隔的关键帧,保持视觉约束,同时仍然遵守IMU项。我们对关键帧的相对不确定性的公式允许在不表达全局姿态不确定性的情况下构建姿态图,灵感来自RSLAM[13]。
2) 我们提供了IMU误差项的完全概率推导,包括相应的信息矩阵,在没有明确引入IMU速率下的状态的情况下关联连续图像帧。
3) 在系统层面,我们开发了用于精确实时SLAM的硬件和算法,包括鲁棒的关键点匹配和使用惯性线索的异常值抑制
在本文的其余部分中,我们在II-B中介绍了批量视觉SLAM中的惯性误差项,然后概述了II-C中的实时立体图像处理和关键帧选择,以及II-D中的边缘化形式。最后,我们在第三章中展示了我们的立体视觉和IMU传感器在室内和室外获得的结果。
紧密耦合视觉-惯性融合
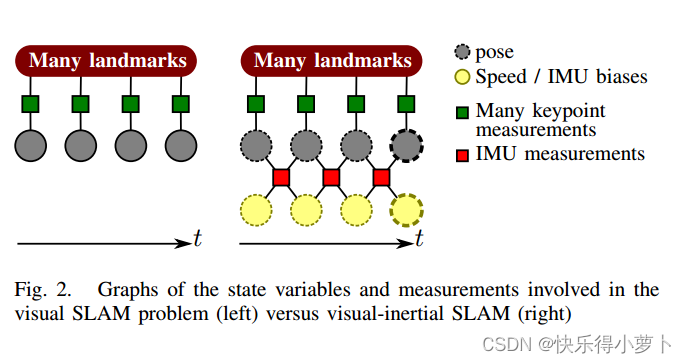
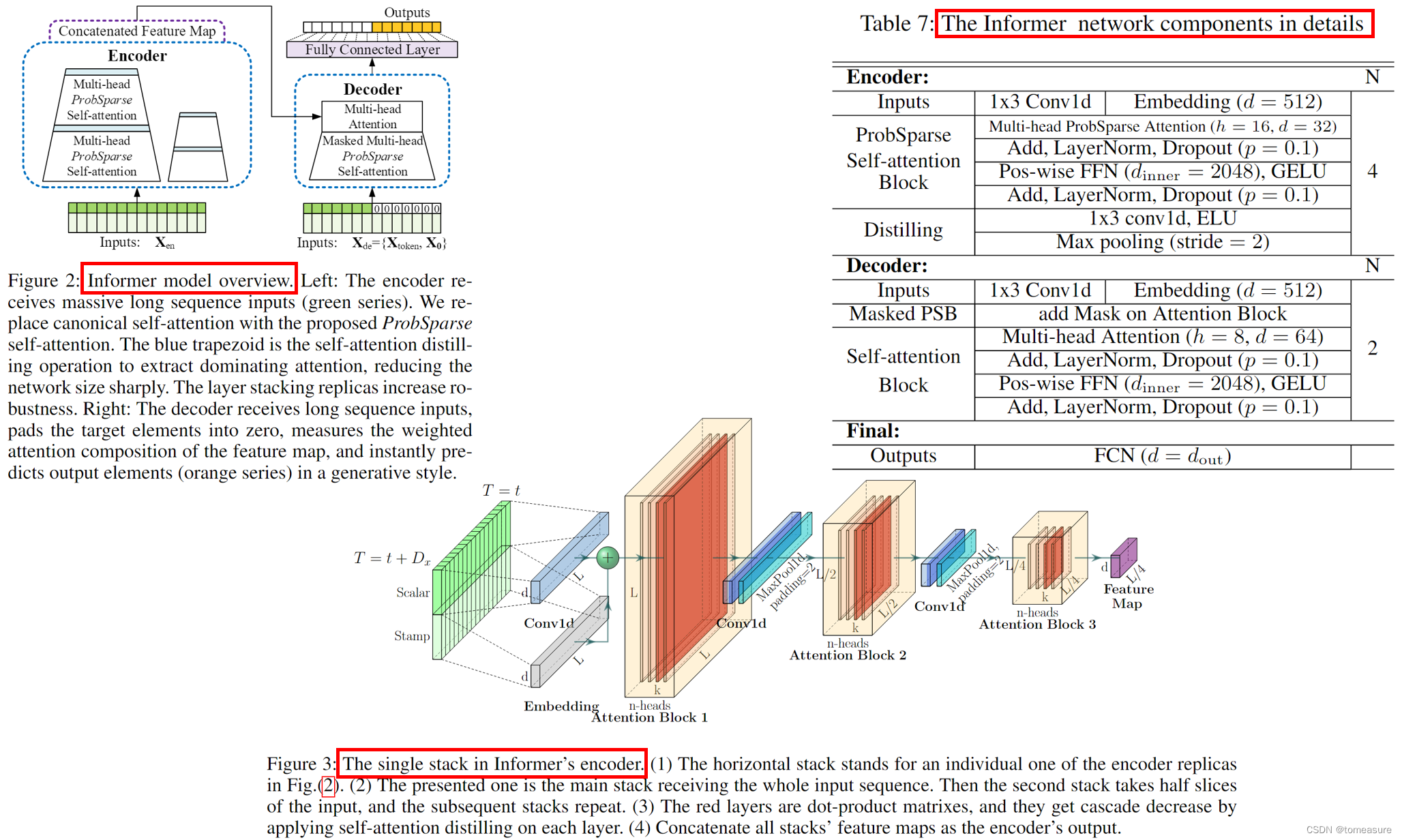
在视觉SLAM中,通过最小化在相机帧中观察到的地标的重投影误差,制定了一种非线性优化来找到相机姿态和地标位置。图2显示了各自的图形表示:它将测量值显示为带有方形框的边,将估计量显示为圆形节点。一旦惯性引入了测量,它们不仅在连续姿态之间产生时间约束,而且在加速度计和陀螺仪的连续速度和IMU偏差估计之间产生时间限制,从而增强机器人状态向量。
在本节中,我们介绍了将惯性测量纳入批量视觉SLAM的方法。
符号和定义
一个帧包含的坐标系
 状态包含
状态包含
x
R
:
=
[
p
W
W
S
T
,
q
W
S
T
,
v
W
W
S
T
,
b
g
T
,
b
a
T
]
T
∈
R
3
×
S
3
×
R
9
\mathbf{x}_{\mathrm{R}}:=\left[\mathbf{p}_W^{W S^T}, \mathbf{q}_{W S}^T, \mathbf{v}_W^{W S^T}, \mathbf{b}_{\mathrm{g}}^T, \mathbf{b}_{\mathrm{a}}^T\right]^T \in \mathbb{R}^3 \times S^3 \times \mathbb{R}^9
xR:=[pWWST,qWST,vWWST,bgT,baT]T∈R3×S3×R9
残差部分
我们试图将视觉惯性定位和映射问题公式化为成本函数
J
(
x
)
J(x)
J(x)的一个联合优化,该成本函数包含来自IMU
e
s
e_s
es的(加权)重投影误差
e
r
e_r
er和时间误差项:
J
(
x
)
:
=
∑
i
=
1
I
∑
k
=
1
K
∑
j
∈
J
(
i
,
k
)
e
r
i
,
j
,
k
W
r
i
,
j
,
k
e
r
i
,
j
,
k
+
∑
k
=
1
K
−
1
e
s
k
T
W
s
k
e
s
k
J(\mathbf{x}):=\sum_{i=1}^I \sum_{k=1}^K \sum_{j \in \mathcal{J}(i, k)} \mathbf{e}_{\mathrm{r}}^{i, j, k} \mathbf{W}_{\mathrm{r}}^{i, j, k} \mathbf{e}_{\mathrm{r}}^{i, j, k}+\sum_{k=1}^{K-1} \mathbf{e}_{\mathrm{s}}^{k^T} \mathbf{W}_{\mathrm{s}}^k \mathbf{e}_{\mathrm{s}}^k
J(x):=i=1∑Ik=1∑Kj∈J(i,k)∑eri,j,kWri,j,keri,j,k+k=1∑K−1eskTWskesk
其中,i是组件的相机索引,k表示相机帧索引,j表示地标索引。
本质上,纯视觉SLAM具有6个自由度(DoF),在优化过程中需要保持固定,即绝对姿态。组合视觉惯性问题只有4个自由度,因为重力使两个旋转自由度可观测到。这使固定变得复杂。我们希望固定围绕重力方向(世界z轴)的偏航,以及第一个位姿的位置 对应4个不可观量。因此,除了设置位置变化为零, δ p W W S k 1 = 0 3 × 1 \delta \mathbf{p}_W^{W S^{k_1}}=\mathbf{0}_{3 \times 1} δpWWSk1=03×1外,我们还假设 δ α k 1 = [ δ α 1 k 1 , δ α 2 k 1 , 0 ] T \delta \boldsymbol{\alpha}^{k_1}=\left[\delta \alpha_1^{k_1}, \delta \alpha_2^{k_1}, 0\right]^T δαk1=[δα1k1,δα2k1,0]T。也就是第一帧的增量进行了处理
在下文中,我们将介绍(标准)重投影误差公式。然后,结合偏置项建模对IMU运动学进行了概述,并在此基础上建立了IMU误差项。
重投影误差公式
e
r
i
,
j
,
k
=
z
i
,
j
,
k
−
h
i
(
T
C
i
S
T
S
W
k
l
W
W
L
,
j
)
\mathbf{e}_{\mathrm{r}}^{i, j, k}=\mathbf{z}^{i, j, k}-\mathbf{h}_i\left(\boldsymbol{T}_{C_i S} \boldsymbol{T}_{S W}^k \boldsymbol{l}_W^{W L, j}\right)
eri,j,k=zi,j,k−hi(TCiSTSWklWWL,j)
imu部分…
关键点匹配和关键帧选择
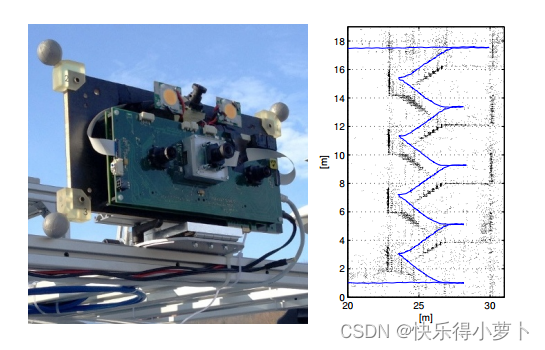
我们的处理流水线采用定制的多尺度SSE优化Harris角检测器,结合BRISK描述符提取[12]。检测器通过逐渐抑制得分较弱的角点来强制图像中的均匀关键点分布,因为它们是在距离较强角点很小的距离处检测到的。描述符是沿着重力方向提取的(投影到图像中),由于紧密的IMU融合,重力方向是可观察的。
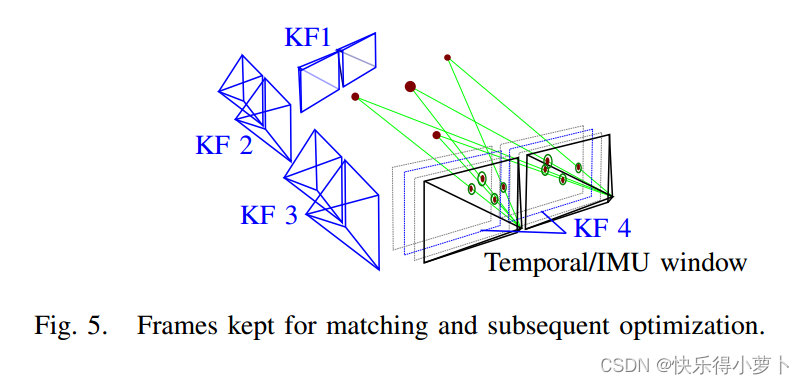
最初,对关键点进行立体三角测量并将其插入到局部地图中。我们针对所有地图地标;通过使用IMU积分获得的(不确定的)姿态预测,在图像坐标中应用卡方检验来简单地执行异常值抑制。不需要昂贵的RANSAC步骤,这是IMU紧密参与的另一个优势。对于子后续优化,保持一组有界的相机帧,即具有在该时刻拍摄的相关图像的姿势;在这些图像中可见的所有地标都保存在本地地图中。如图5所示,我们区分了两种帧:我们引入了包括当前帧在内的S个最近帧的时间窗口;并且我们使用了许多N个关键帧,这些关键帧可能在很久以前就被拍摄过。对于关键帧选择,我们使用一个简单的启发式方法:如果匹配点跨越的图像区域与所有检测点跨越的区域之间的比率低于50%到60%,则帧被标记为关键帧。
部分边缘化
非线性时间约束如何存在于包含关键帧的有界优化窗口中尚不清楚,这些关键帧可能在时间上间隔任意远。在下文中,我们首先提供了边缘化的数学基础,即非线性优化中状态的消除,并将其应用于视觉惯性SLAM。
1) 非线性优化中边缘化的数学公式:
高斯-牛顿方程组由所有误差项、雅可比矩阵和信息构成:其形式为
H
δ
χ
=
b
Hδχ=b
Hδχ=b。让我们考虑一组待边缘化的状态,
x
µ
x_µ
xµ,与误差项相关的所有状态的集合,
x
λ
x_λ
xλ,以及剩余状态的集合
x
ρ
x_ρ
xρ。由于条件独立性,我们可以简化边缘化步骤,只将其应用于一个子问题:
[
H
μ
μ
H
μ
λ
1
H
λ
1
μ
H
λ
1
λ
1
]
[
δ
χ
μ
δ
χ
λ
]
=
[
b
μ
b
λ
1
]
\left[\begin{array}{cc} \mathbf{H}_{\mu \mu} & \mathbf{H}_{\mu \lambda_1} \\ \mathbf{H}_{\lambda_1 \mu} & \mathbf{H}_{\lambda_1 \lambda_1} \end{array}\right]\left[\begin{array}{l} \delta \boldsymbol{\chi}_\mu \\ \delta \boldsymbol{\chi}_\lambda \end{array}\right]=\left[\begin{array}{c} \mathbf{b}_\mu \\ \mathbf{b}_{\lambda_1} \end{array}\right]
[HμμHλ1μHμλ1Hλ1λ1][δχμδχλ]=[bμbλ1]
Schur互补运算的应用产生:
H
λ
1
λ
1
∗
:
=
H
λ
1
λ
1
−
H
λ
1
μ
H
μ
μ
−
1
H
μ
λ
1
b
λ
1
∗
:
=
b
λ
1
−
H
λ
1
μ
H
μ
μ
−
1
b
μ
\begin{aligned} \mathbf{H}_{\lambda_1 \lambda_1}^* & :=\mathbf{H}_{\lambda_1 \lambda_1}-\mathbf{H}_{\lambda_1 \mu} \mathbf{H}_{\mu \mu}^{-1} \mathbf{H}_{\mu \lambda_1} \\ \mathbf{b}_{\lambda_1}^* & :=\mathbf{b}_{\lambda_1}-\mathbf{H}_{\lambda_1 \mu} \mathbf{H}_{\mu \mu}^{-1} \mathbf{b}_\mu \end{aligned}
Hλ1λ1∗bλ1∗:=Hλ1λ1−Hλ1μHμμ−1Hμλ1:=bλ1−Hλ1μHμμ−1bμ
(18)中的方程式描述了边缘化的单一步骤。在我们基于关键帧的方法中,必须重复应用边缘化步骤,并随着状态估计的不断变化,将得到的信息作为优化的先验信息。因此,我们将线性化点固定在x0附近,即边缘化时x的值。有限偏差
Δ
χ
:
=
Φ
−
1
(
log
(
x
‾
⊞
x
0
−
1
)
)
)
\left.\Delta \chi:=\Phi^{-1}\left(\log \left(\overline{\mathbf{x}} \boxplus \mathbf{x}_0^{-1}\right)\right)\right)
Δχ:=Φ−1(log(x⊞x0−1)))表示边缘化后发生的状态更新,其中
x
‾
\overline{\mathbf{x}}
x是我们对x的当前估计。换句话说,x由
x
=
exp
(
Φ
(
δ
χ
)
)
⊞
exp
(
Φ
(
Δ
χ
)
)
⊞
x
0
⏟
=
x
‾
.
\mathbf{x}=\exp (\Phi(\delta \boldsymbol{\chi})) \boxplus \underbrace{\exp (\Phi(\Delta \boldsymbol{\chi})) \boxplus \mathbf{x}_0}_{=\overline{\mathbf{x}}} .
x=exp(Φ(δχ))⊞=x
exp(Φ(Δχ))⊞x0.这种通用公式允许我们将最小坐标上的先验信息应用于任何状态变量,包括单位长度四元数。引入∆χ可以将右手边近似为(一阶)
b
+
∂
b
∂
Δ
χ
∣
x
0
Δ
χ
=
b
−
H
Δ
χ
\mathbf{b}+\left.\frac{\partial \mathbf{b}}{\partial \Delta \boldsymbol{\chi}}\right|_{\mathbf{x}_0} \Delta \boldsymbol{\chi}=\mathbf{b}-\mathbf{H} \Delta \boldsymbol{\chi}
b+∂Δχ∂b
x0Δχ=b−HΔχ现在我们可以将高斯-牛顿系统(17)表示为:
[
b
μ
b
λ
1
]
=
[
b
μ
,
0
b
λ
1
,
0
]
−
[
H
μ
μ
H
μ
λ
1
H
λ
1
μ
H
λ
1
λ
1
]
[
Δ
χ
μ
Δ
χ
λ
]
.
\left[\begin{array}{c} \mathbf{b}_\mu \\ \mathbf{b}_{\lambda_1} \end{array}\right]=\left[\begin{array}{c} \mathbf{b}_{\mu, 0} \\ \mathbf{b}_{\lambda_1, 0} \end{array}\right]-\left[\begin{array}{cc} \mathbf{H}_{\mu \mu} & \mathbf{H}_{\mu \lambda_1} \\ \mathbf{H}_{\lambda_1 \mu} & \mathbf{H}_{\lambda_1 \lambda_1} \end{array}\right]\left[\begin{array}{c} \Delta \boldsymbol{\chi}_\mu \\ \Delta \boldsymbol{\chi}_\lambda \end{array}\right] .
[bμbλ1]=[bμ,0bλ1,0]−[HμμHλ1μHμλ1Hλ1λ1][ΔχμΔχλ].
在这种形式中,右侧(18)变成
b
λ
1
∗
=
b
λ
1
,
0
−
H
λ
1
μ
T
H
μ
μ
−
1
b
μ
,
0
⏟
b
λ
1
,
0
∗
−
H
λ
1
λ
1
∗
Δ
χ
λ
1
.
\mathbf{b}_{\lambda_1}^*=\underbrace{\mathbf{b}_{\lambda_1, 0}-\mathbf{H}_{\lambda_1 \mu}^T \mathbf{H}_{\mu \mu}^{-1} \mathbf{b}_{\mu, 0}}_{\mathbf{b}_{\lambda_1, 0}^*}-\mathbf{H}_{\lambda_1 \lambda_1}^* \Delta \chi_{\lambda_1} .
bλ1∗=bλ1,0∗
bλ1,0−Hλ1μTHμμ−1bμ,0−Hλ1λ1∗Δχλ1.
在边缘化节点包括无穷大(或足够接近无穷大)处的地标,或仅在一个相机中从单个姿势可见的地标的情况下,与这些地标相关联的Hessian块将(在数值上)等级不足。因此,我们采用了伪逆
H
µµ
+
H^+_{µµ}
Hµµ+,它为给定
δ
χ
λ
δχ_λ
δχλ的
δ
χ
µ
δχ_µ
δχµ提供了一个零分量到零空间方向的解
上述公式为边缘化的状态 x µ x_µ xµ和剩余状态 x λ x_λ xλ引入了一个固定的线性化点。这也将被用作涉及这些状态的术语的所有未来线性化的参考点。在应用(18)之后,我们可以去除消耗的非线性项,并将边缘化的 H λ 1 λ 1 ∗ , N \mathbf{H}_{\lambda_1 \lambda_1}^{*, N} Hλ1λ1∗,N 和 b λ 1 ∗ , N \mathbf{b}_{\lambda_1}^{*, N} bλ1∗,N,作为求和项,以构建整个高斯-牛顿系统。对平方误差的贡献可以写成 χ λ 1 2 = b λ 1 ∗ T H λ 1 λ 1 ∗ + b λ 1 ∗ \chi_{\lambda_1}^2=\mathbf{b}_{\lambda_1}^{* T} \mathbf{H}_{\lambda_1 \lambda_1}^{*+} \mathbf{b}_{\lambda_1}^* χλ12=bλ1∗THλ1λ1∗+bλ1∗.
边缘化应用于基于关键帧的视觉惯性SLAM:
最初边缘化的误差项是由前N+1帧
x
T
k
,
k
=
1
,
…
,
N
+
1
\mathbf{x}_{\mathrm{T}}^k, k=1, \ldots, N+1
xTk,k=1,…,N+1构造的。分别具有如图6所示的速度和偏置状态。N个第一帧将全部解释为关键帧,边缘化步骤包括消除相应的速度和偏移状态。

当一个新的帧
x
T
c
x^c_T
xTc(当前帧,索引c)被插入到优化窗口中时,我们应用边缘化操作。在时间窗口
(
x
T
c
−
S
)
(x^{ c−S}_ T)
(xTc−S)中最古老的帧不是关键帧的情况下,我们将放弃其所有路标点测量,然后将其与最古老的速度和偏移状态一起边缘化。图7说明了这个过程。丢弃路标测量是次优的;
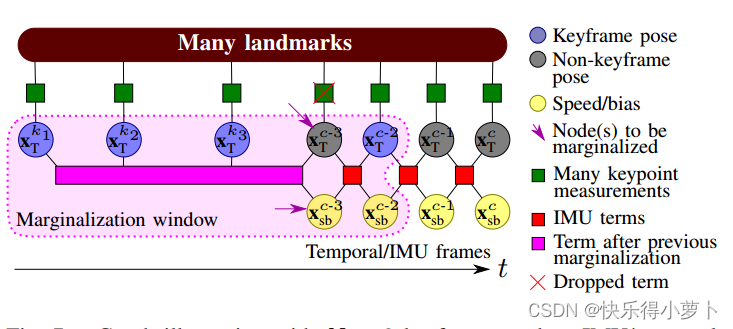 图7、具有N=3个关键帧和IMU/时间节点大小S=3的图形说明。一个规则的框架正在从时间窗口中滑出。
图7、具有N=3个关键帧和IMU/时间节点大小S=3的图形说明。一个规则的框架正在从时间窗口中滑出。
然而,为了快速求解,它保持了问题的稀疏性。具有关键帧的视觉SLAM成功地以类似的方式进行,丢弃具有路标测量值的整个帧。
在
(
x
T
c
−
S
)
(x^{ c−S}_ T)
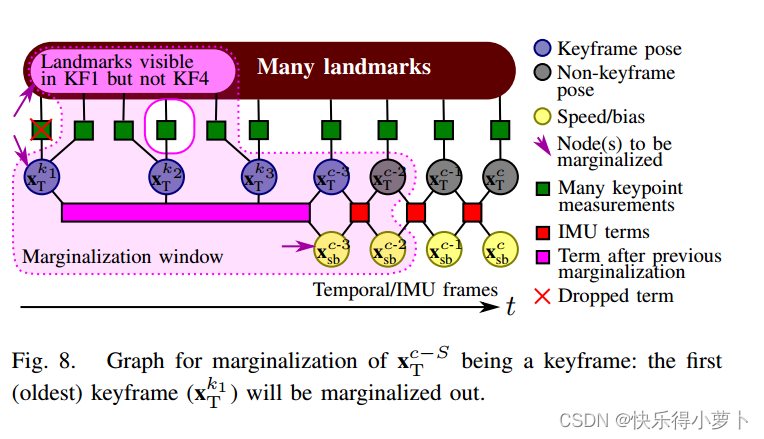
(xTc−S)是关键帧的情况下,简单地放弃所有关键点测量的信息损失将更为显著:公共路标点观测中编码的最古老的两个关键帧之间的所有相对姿态信息都将丢失。因此,我们还将在
x
T
k
1
x^{k1}_T
xTk1中可见但在最近的关键帧中不可见的地标边缘化。图8以图形方式描述了该过程。问题的稀疏性再次得到保留。
总结
本文提出了一种将惯性测量紧密集成到基于关键帧的视觉SLAM中的方法。非线性优化中误差项的组合是由可用于关键点检测和IMU读数的误差统计数据驱动的,从而取代了对任何调谐参数的需要。使用所提出的方法,我们使用IMU运动学运动模型获得了重力方向的全局一致性和鲁棒的异常点抑制。同时,获得了基于关键帧的非线性优化的所有优点,如保持静止的姿态。使用立体相机和IMU传感器获得的结果证明了所提出的框架的实时操作,同时比仅视觉或松耦合方法表现出更高的准确性和鲁棒性。