论文:《Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting》
代码:https://github.com/zhouhaoyi/Informer2020
地址:https://arxiv.org/abs/2012.07436v3
特点:
- 实现时间与空间复杂度为 O ( L ln L ) \mathcal{O}(L\ln L) O(LlnL) 的自注意力;
- 使用自注意力提纯(Distilling)的方法,降低了特征的冗余;
- 以生成式的风格一次性输出长序列预测结果,杜绝了 One-by-One 方式中存在的误差积累;
- 基于上面的内容,创建新的 LSTF 模型 Informer。
核心贡献:
- 用新的自注意力模块 ProbSparse Self-Attention 降低了原始 Self-Attention 的时间与空间复杂度;
- 提出 Self-Attention 净化(Distilling) 方法,进一步降低模型整体的复杂度;
Informer 模型的整体结构
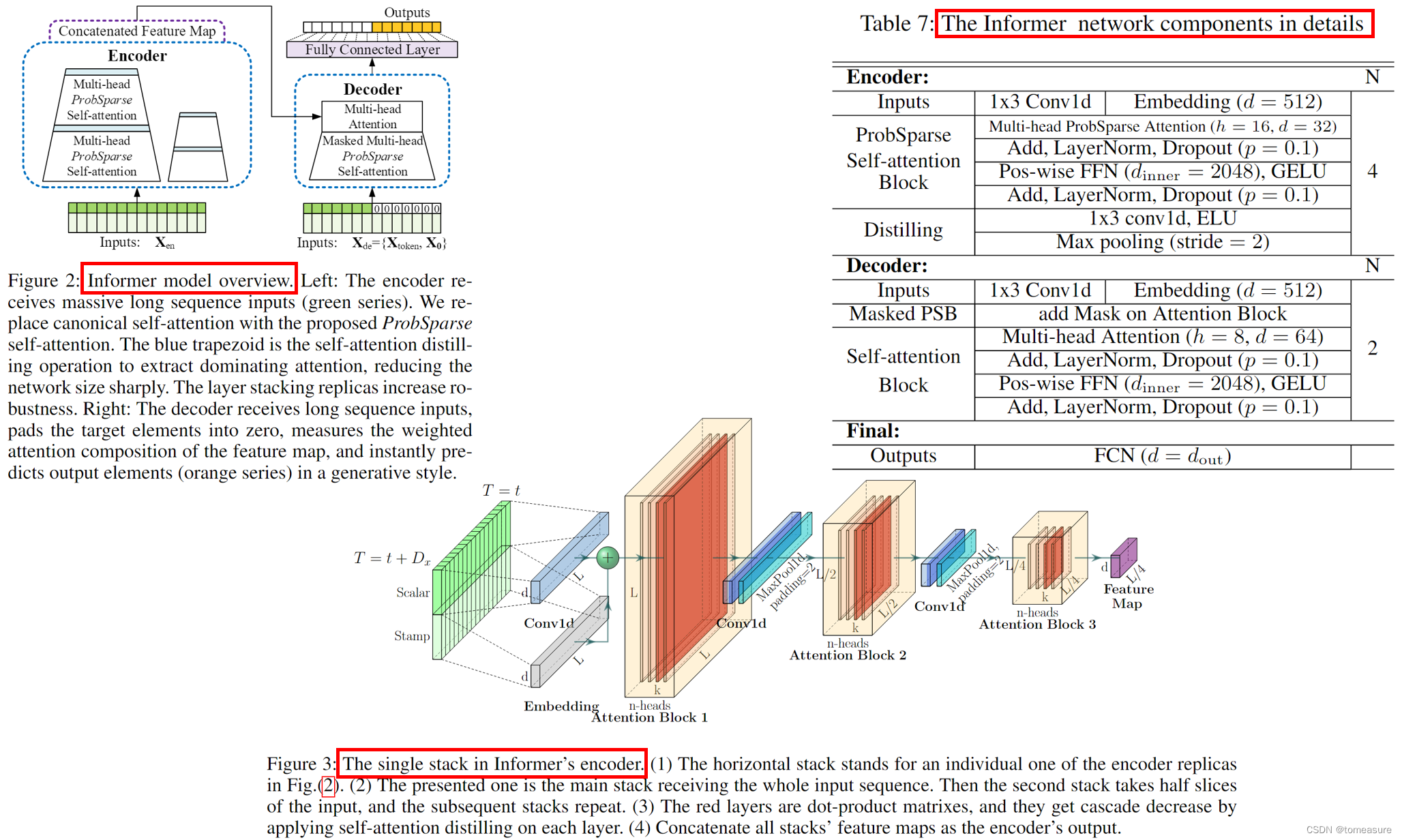
ProbSparse Self-Attention
先介绍一下算法的整体流程,后面再介绍具体含义和原因。
Require:Tensor Q ∈ R m × d , K ∈ R n × d , V ∈ R n × d \pmb{Q}\in\mathbb{R}^{m\times d},\pmb{K}\in\mathbb{R}^{n\times d},\pmb{V}\in\mathbb{R}^{n\times d} Q∈Rm×d,K∈Rn×d,V∈Rn×d
- print set hyperparameter c c c, u = c ln m u=c\ln m u=clnm and U = m ln n U=m\ln n U=mlnn
- randomly select U U U dot-product pairs from K \pmb{K} K to K ˉ \bar{\pmb{K}} Kˉ
- set the sample score S ˉ = Q K ˉ T \bar{\pmb{S}}=\pmb{Q}\bar{\pmb{K}}^T Sˉ=QKˉT
- compute the measurement M = max ( S ˉ ) − mean ( S ˉ ) M=\max(\bar{\pmb{S}})-\text{mean}(\bar{\pmb{S}}) M=max(Sˉ)−mean(Sˉ) by row
- set Top- u \text{Top-}u Top-u queries under M M M as Q ˉ \bar{\pmb{Q}} Qˉ
- set S 1 = softmax ( Q ˉ K T / d ) ⋅ V \pmb{S}_1=\text{softmax}(\bar{\pmb{Q}}\pmb{K}^T/\sqrt{d})\cdot \pmb{V} S1=softmax(QˉKT/d)⋅V
- set S 0 = mean ( V ) \pmb{S}_0=\text{mean}(\pmb{V}) S0=mean(V)
- set S = { S 1 , S 0 } \pmb{S}=\{\pmb{S}_1,\pmb{S}_0\} S={S1,S0} by their original rows accordingly
Ensure:self-attention feature map S \pmb{S} S
ProbSparse Self-Attention 的基本思想
利用原始 Self-Attention 中的稀疏性,降低算法的时间与空间复杂度。
核心方法:利用下式选出对 value 更有价值的 query
M ˉ ( q i , K ) = max j { q i k j T d } − 1 L K Σ j = 1 L K q i k j T d \bar{M}(\pmb{q}_i,\pmb{K})=\max_{j}\{\frac{\pmb{q}_i\pmb{k}_j^T}{\sqrt{d}}\}-\frac{1}{L_K}\Sigma^{L_K}_{j=1}\frac{\pmb{q}_i\pmb{k}_j^T}{\sqrt{d}} Mˉ(qi,K)=jmax{dqikjT}−LK1Σj=1LKdqikjT
即算法中的 3 与 4。
为什么用这种方法?:
原始 Self-Attention
softmax
(
Q
K
T
/
d
)
⋅
V
\text{softmax}(\pmb{Q}\pmb{K}^T/\sqrt{d})\cdot \pmb{V}
softmax(QKT/d)⋅V 可改写为下面的概率形式:
A
(
q
i
,
K
,
V
)
=
Σ
j
k
(
q
i
,
k
j
)
Σ
l
k
(
q
i
,
k
l
)
v
j
=
E
p
(
k
j
∣
q
i
)
[
v
j
]
\mathcal{A}(\pmb{q}_i,\pmb{K},\pmb{V})=\Sigma_j\frac{k(\pmb{q}_i,\pmb{k}_j)}{\Sigma_l k(\pmb{q}_i,\pmb{k}_l)}\pmb{v}_j=\mathbb{E}_{p(\pmb{k}_j|\pmb{q}_i)}[\pmb{v}_j]
A(qi,K,V)=ΣjΣlk(qi,kl)k(qi,kj)vj=Ep(kj∣qi)[vj]
k ( ⋅ , ⋅ ) k(\cdot,\cdot) k(⋅,⋅) 的含义不再赘述。
为度量 query 的稀疏性,可以考虑
p
(
k
j
∣
q
i
)
p(\pmb{k}_j|\pmb{q}_i)
p(kj∣qi) 与均匀分布
q
(
k
j
∣
q
i
)
=
1
/
L
K
q(\pmb{k}_j|\pmb{q}_i)=1/L_K
q(kj∣qi)=1/LK`之间的 KL 散度
K
L
(
q
∣
∣
p
)
=
−
Σ
1
L
K
ln
(
k
(
q
i
,
k
j
)
Σ
l
k
(
q
i
,
k
l
)
L
K
)
KL(q||p)=-\Sigma\frac{1}{L_K}\ln(\frac{k(\pmb{q}_i,\pmb{k}_j)}{\Sigma_l k(\pmb{q}_i,\pmb{k}_l)}L_K)
KL(q∣∣p)=−ΣLK1ln(Σlk(qi,kl)k(qi,kj)LK),展开并舍弃常数项之后可得第 i 个 query 的稀疏性度量为:
M
(
q
i
,
K
)
=
ln
Σ
j
=
1
L
K
e
q
i
k
j
T
d
−
1
L
K
Σ
j
=
1
L
K
q
i
k
j
T
d
M(\pmb{q}_i,\pmb{K})=\ln\Sigma^{L_K}_{j=1}e^{\frac{\pmb{q}_i\pmb{k}^T_j}{\sqrt{d}}}-\frac{1}{L_K}\Sigma^{L_K}_{j=1}\frac{\pmb{q}_i\pmb{k}^T_j}{\sqrt{d}}
M(qi,K)=lnΣj=1LKedqikjT−LK1Σj=1LKdqikjT
基于 M,可以选用 Top-u 的 queries 构成的 Q ˉ \bar{\pmb{Q}} Qˉ 代替 Q 计算自注意力(文中设置 u = c ln L Q u=c\ln L_Q u=clnLQ,其中 c 是超参数)。
为什么要使用这两个分布的 KL 散度?为什么M可以度量注意力的稀疏性?:Self-Attention 涉及到了点积运算,该运算表明 p ( k j ∣ q i ) p(\pmb{k}_j|\pmb{q}_i) p(kj∣qi) 与均匀分布 q ( k j ∣ q i ) = 1 / L K q(\pmb{k}_j|\pmb{q}_i)=1/L_K q(kj∣qi)=1/LK 之间的差别越大越好,这启发我们使用 M 作为稀疏性的度量。
新问题:M 中的第一项实际计算时的复杂度仍旧是 O ( L 2 ) \mathcal{O}(L^2) O(L2) 的。
解决方式:基于 Lemma 1 与 Proposition 1,先随机采样 U = L K ln L Q U=L_K\ln L_Q U=LKlnLQ 个 k-q 对,然后在这 U 个 k-q 对上计算 M ˉ = max j { q i k j T d } − mean j { q i k j T d } \bar{M}=\max_{j}\{\frac{\pmb{q}_i\pmb{k}^T_j}{\sqrt{d}}\}-\text{mean}_{j}\{\frac{\pmb{q}_i\pmb{k}^T_j}{\sqrt{d}}\} Mˉ=maxj{dqikjT}−meanj{dqikjT} 作为 M 的近似值,最后选定 top-u 个 query 用作 Self-Attention 计算。(即算法中的 1、2、5 和 6,这里两次降低计算量)补充:
- Lemma 1:For each query q i ∈ R d \pmb{q}_i\in\mathbb{R}^d qi∈Rd and k j ∈ R d \pmb{k}_j\in\mathbb{R}^d kj∈Rd in the keys set K \pmb{K} K, we have the bound as ln L K ≤ M ( q i , K ) ≤ ln L K + M ˉ ( q i , K ) \ln L_K\leq M(\pmb{q}_i,\pmb{K})\leq\ln L_K +\bar{M}(\pmb{q}_i,\pmb{K}) lnLK≤M(qi,K)≤lnLK+Mˉ(qi,K). When q i ∈ K \pmb{q}_i\in\pmb{K} qi∈K, it also holds.(它说明可以用 M ˉ \bar{M} Mˉ 做近似计算。利用凸函数证明)
- Proposition 1: Assuming k j ∼ N ( μ , Σ ) \pmb{k}_j\sim\mathcal{N}(\mu,\Sigma) kj∼N(μ,Σ) and we let q k i \pmb{q}\pmb{k}_i qki denote set { ( q i k j T ) / d ∣ j = 1 , ⋯ , L K } \{(\pmb{q}_i\pmb{k}_j^T)/\sqrt{d}|j=1,\cdots,L_K\} {(qikjT)/d∣j=1,⋯,LK}, then ∀ M m = max i M ( q i , K ) \forall M_m=\max_i M(\pmb{q}_i,\pmb{K}) ∀Mm=maxiM(qi,K) there exist κ > 0 \kappa>0 κ>0 such that: in the interval ∀ q 1 , q 2 ∈ { q ∣ M ( q , K ) ∈ [ M m , M m − κ ) } \forall\pmb{q}_1,\pmb{q}_2\in\{\pmb{q}|M(\pmb{q},\pmb{K})\in[M_m,M_m-\kappa)\} ∀q1,q2∈{q∣M(q,K)∈[Mm,Mm−κ)}, if M ˉ ( q 1 , K ) > M ˉ ( q 2 , K ) \bar{M}(\pmb{q}_1,\pmb{K})>\bar{M}(\pmb{q}_2,\pmb{K}) Mˉ(q1,K)>Mˉ(q2,K) and Var ( q k 1 ) > Var ( q k 2 ) \text{Var}(\pmb{q}\pmb{k}_1)>\text{Var}(\pmb{q}\pmb{k}_2) Var(qk1)>Var(qk2), we have high probability that M ( q 1 , K ) > M ( q 2 , K ) M(\pmb{q}_1,\pmb{K})>M(\pmb{q}_2,\pmb{K}) M(q1,K)>M(q2,K).(采样后不影响排序,这说明采样之后仍旧可以保证 Top-u 的可靠性。利用对数正态分布及数值化样例定性式证明)
Self-Attention Distilling
目的:在自注意力模块之后,过滤掉 value 中的冗余信息。
方式:使用 CNN、MaxPooling 进行下采样:
\pmb{X}^t_{j+1}=\text{MaxPool}(\text{ELU}(\text{Conv1d}([\pmb{X}^t_j]_{AB})))
其中,CNN 的 kernel-size=3,pooling 的 stride=2,整体的空间复杂度为: O ( ( 2 − ϵ ) L log L ) \mathcal{O}((2-\epsilon)L\log L) O((2−ϵ)LlogL), ϵ \epsilon ϵ 是一个小量(原因是: 1 + 1 2 + 1 4 + 1 8 + ⋯ 1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\cdots 1+21+41+81+⋯)。
其他
- Decoder:与原始 Transformer 的一致;
- 生成式推断(Generative Inference):一次性输出长序列预测结果,而非迭代地逐个输出结果。
- Loss Function:MSE
- 位置嵌入(Position Embedding):局部时间戳的位置嵌入(PE,使用sin函数)、全局时间戳的位置嵌入(SE,用于日月周节日等特殊时间点)
PE
(
L
x
×
(
t
−
1
)
+
i
,
)
+
Σ
[
SE
(
L
x
×
(
t
−
1
)
+
i
)
]
p
\text{PE}_{(L_x\times(t-1)+i,)}+\Sigma[\text{SE}_{(L_x\times(t-1)+i)}]_p
PE(Lx×(t−1)+i,)+Σ[SE(Lx×(t−1)+i)]p
# PE pe[:, 0::2] = torch.sin(position * div_term) pe[:, 1::2] = torch.cos(position * div_term) # SE minute_x = nn.Embedding( 4, d_model)(x[:,:,4]) hour_x = nn.Embedding(24, d_model)(x[:,:,3]) weekday_x = nn.Embedding( 7, d_model)(x[:,:,2]) day_x = nn.Embedding(32, d_model)(x[:,:,1]) month_x = nn.Embedding(13, d_model)(x[:,:,0]) se = hour_x + weekday_x + day_x + month_x + minute_x