数据结构空间复杂度
- 空间复杂度
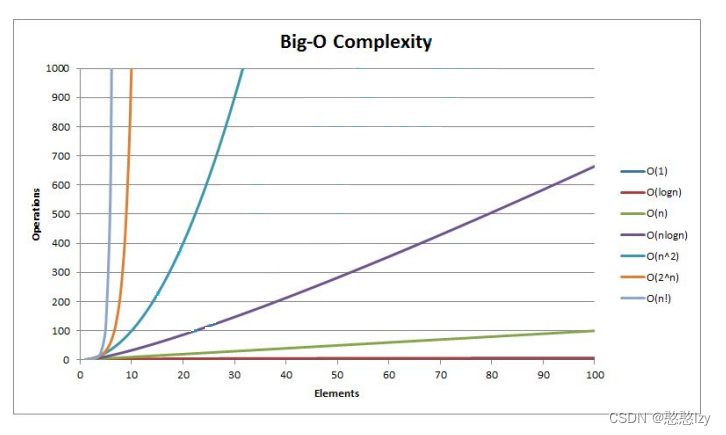
- 常见的复杂度对比
空间复杂度
空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时额外占用存储空间大小的量度 。
空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。
空间复杂度计算规则基本跟实践复杂度类似,也使用大O渐进表示法。
注意:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。
实例1:
// 计算BubbleSort的空间复杂度?
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i-1] > a[i])
{
Swap(&a[i-1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}
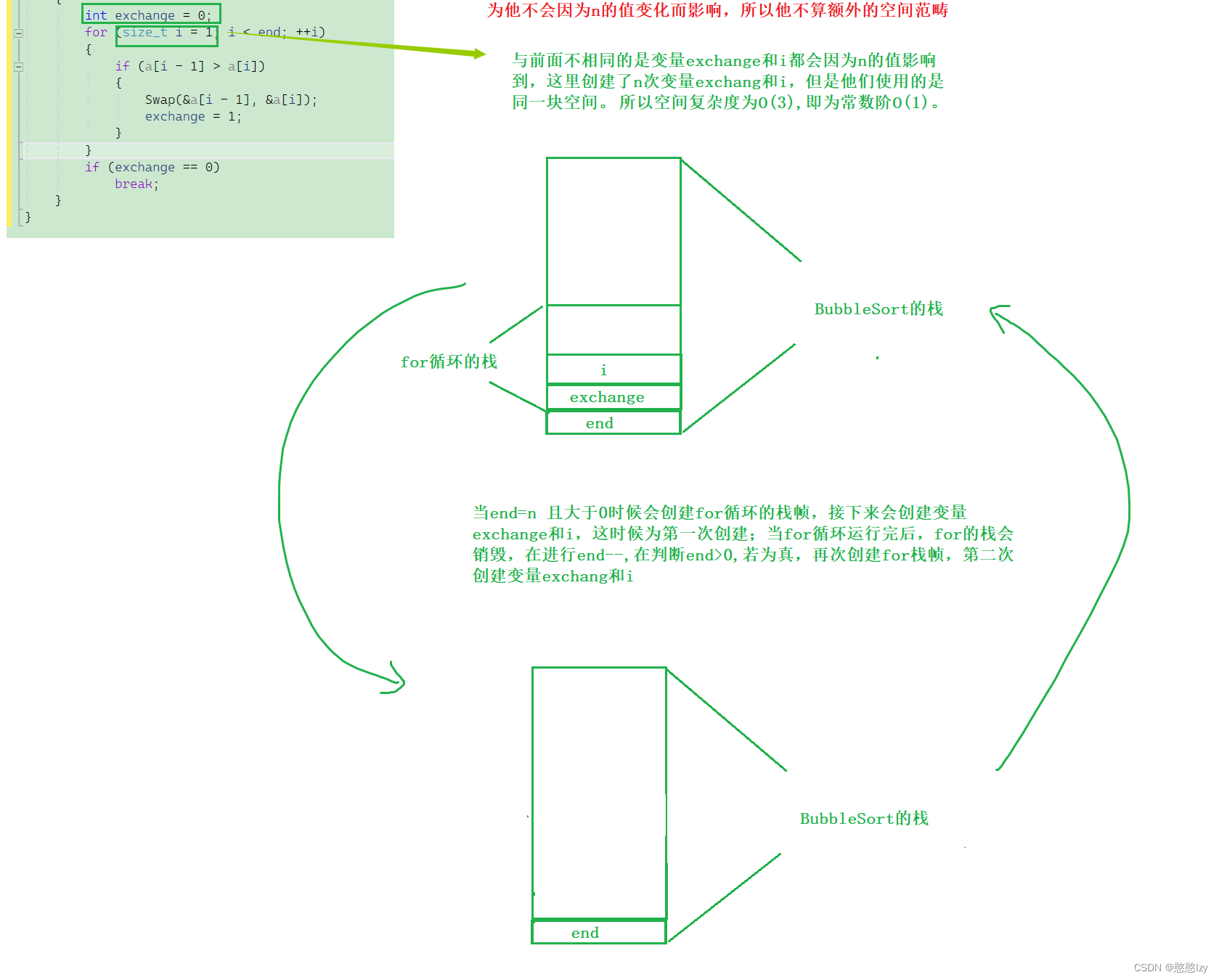
故空间复杂度为O(1)
例2:
// 计算Fibonacci的空间复杂度?
// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n)
{
if(n==0)
return NULL;
long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));
fibArray[0] = 0;
fibArray[1] = 1;
for (int i = 2; i <= n ; ++i)
{
fibArray[i] = fibArray[i - 1] + fibArray [i - 2];
}
return fibArray;
}

空间复杂度为O(N)
例3:
// 计算阶乘递归Fac的空间复杂度?
long long Fac(size_t N)
{
if(N == 0)
return 1;
return Fac(N-1)*N;
}

空间复杂度O(N)
例4:
//计算斐波那契递归Fib的空间复杂度
//long long Fib(size_t N)
//{
// if (N < 3)
// return 1;
//
// return Fib(N - 1) + Fib(N - 2);
//}
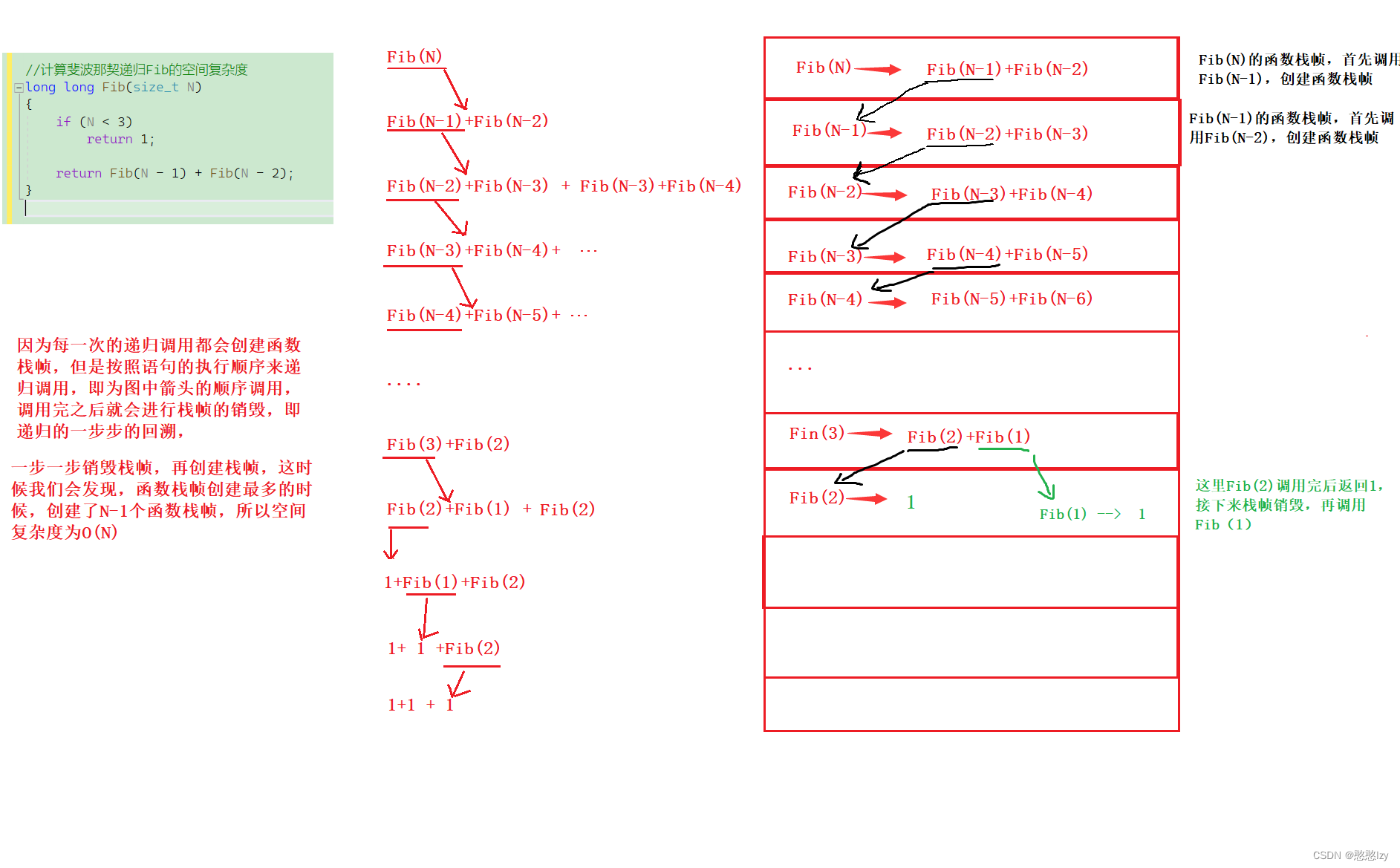
所以空间复杂度为O(N)
常见的复杂度对比
| 5201314 | O(1) | 常数阶 |
|---|---|---|
| 3N+4 | O(N) | 线性阶 |
| 3N2+4N+5 | O(N2) | 平方阶 |
| 3log2N+4 | O(logN) | 对数阶 |
| 2N+3nlogN+14 | O(NlogN ) | NlogN阶 |
| N3+2N2+4N+5 | O(N3) | 立方阶 |
| 2N | O(2N) | 指数阶 |