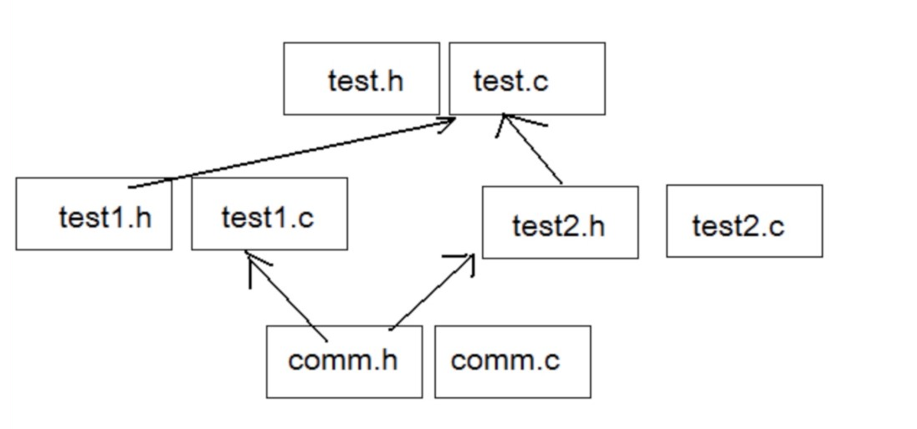
官方文档:OpenMP | LLNL HPC Tutorials
OpenMP总览
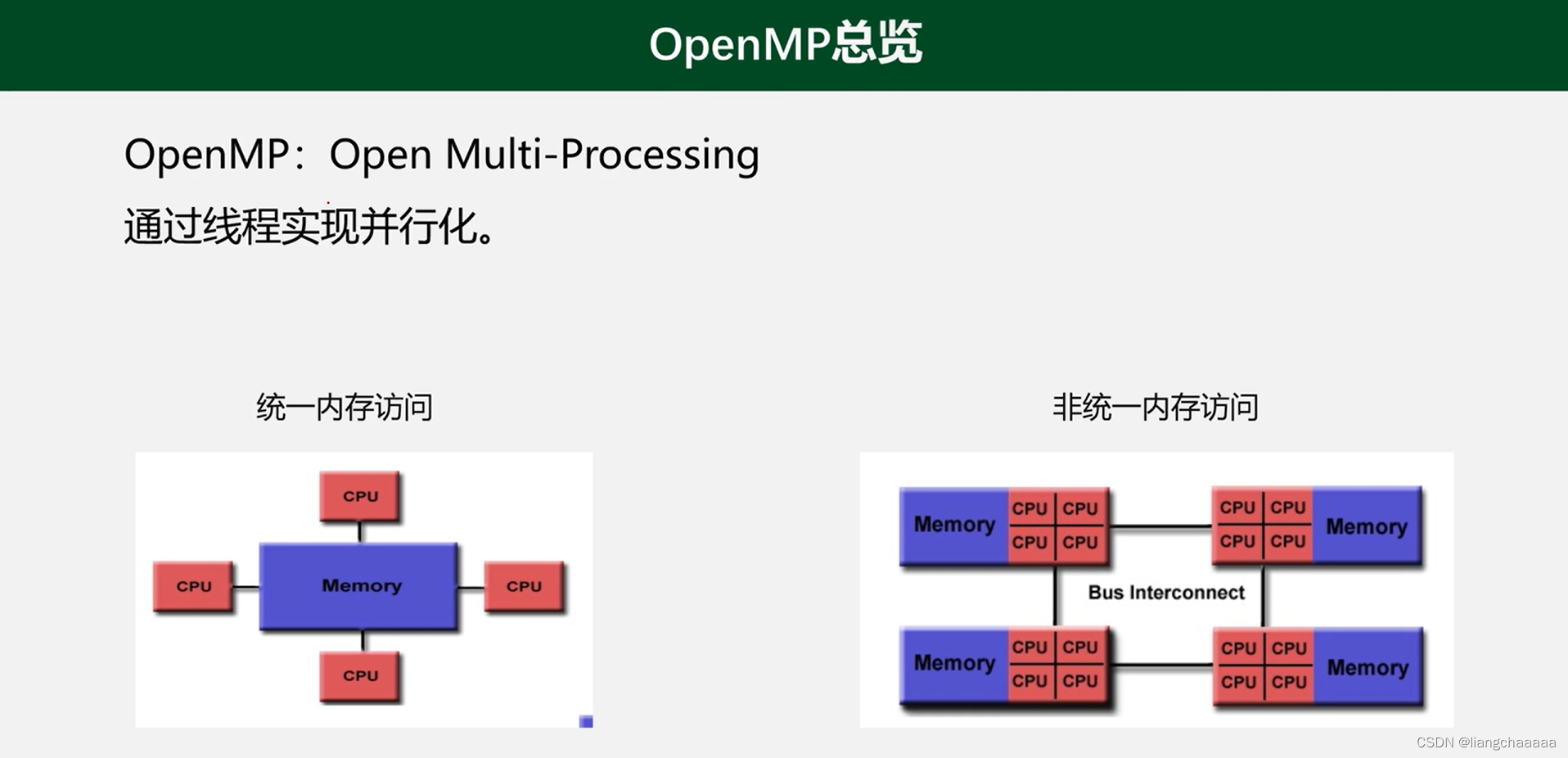
统一内存访问:OpenMP、Pthreads
非统一内存访问:MPI
OpenMP与Pthread

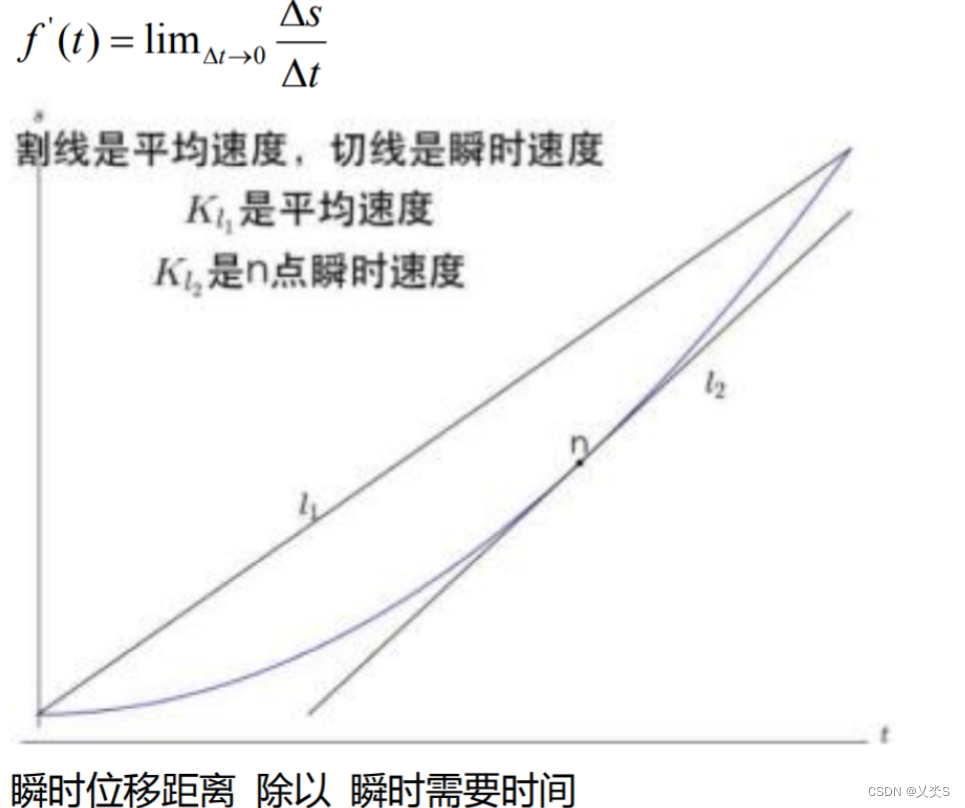
OpenMP原理
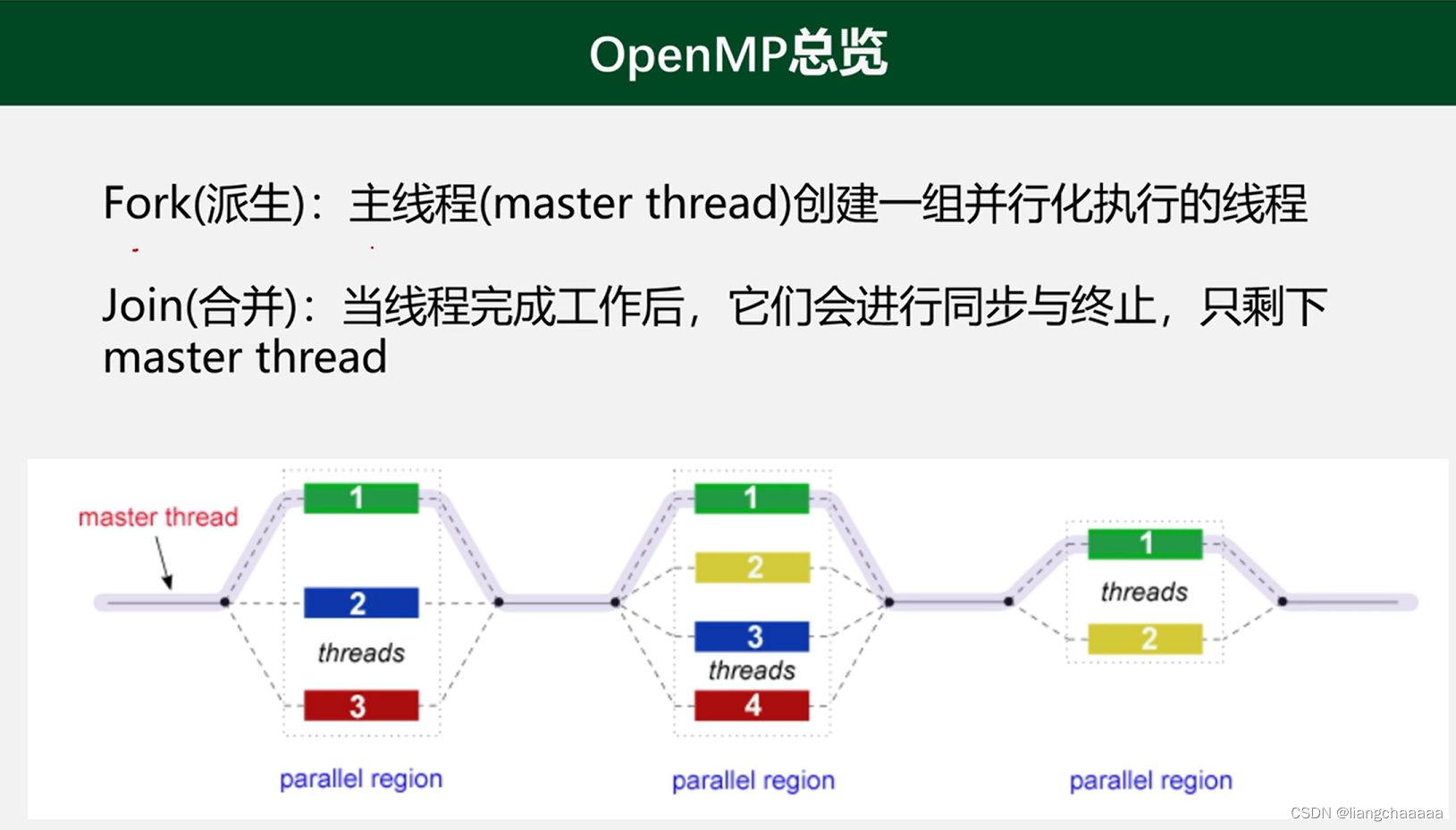
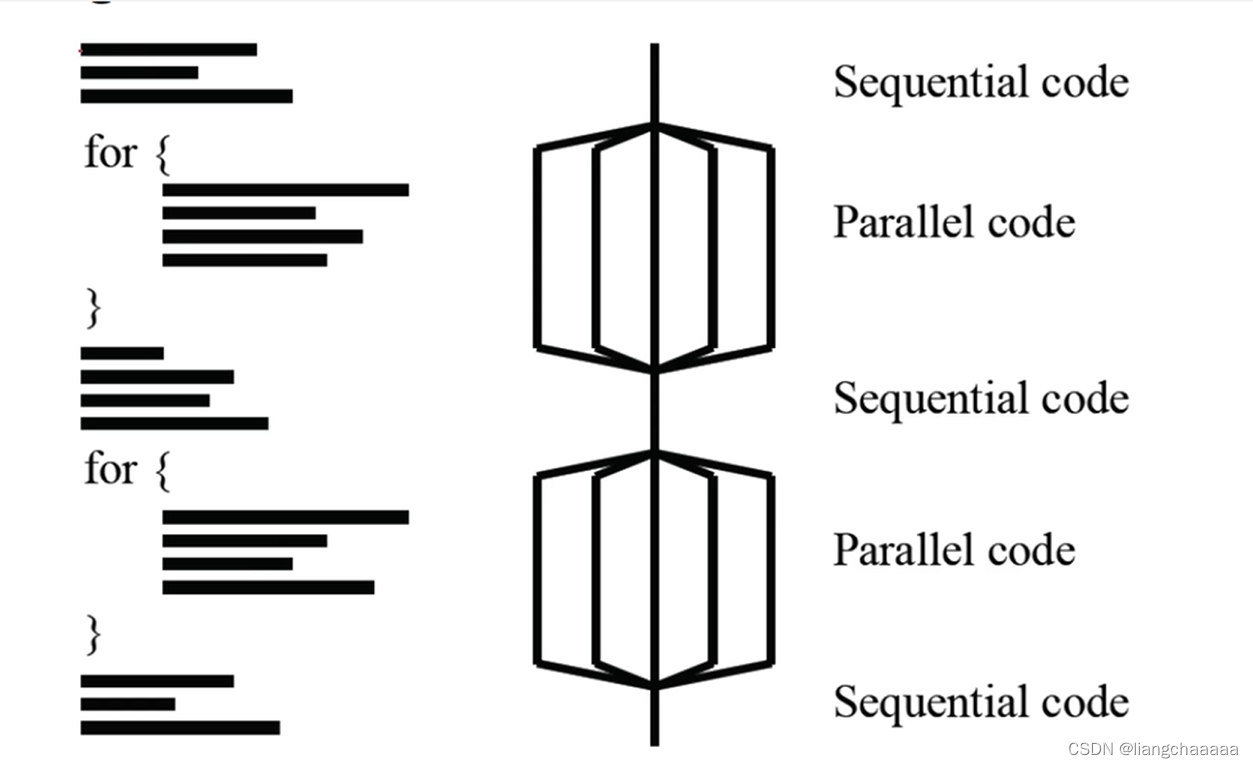
串行区到达并行区后会派生多个线程,并行区代码执行完后进行线程合并,剩下主线程
编译指导语句格式
openmp提供基于指令的内存共享API
预处理指令:#pragma omp 指导指令 [子句]
若一行放不下要另起一行,则需要 / 来转义
编译指令:gcc -g -fopenmp -o hello hello.c
没有代码补全了,很急啊!!!
示例程序
“Hello world”
#include<stdlib.h>
#include<stdio.h>
#ifdef _OPENMP
#include<omp.h>
#endif
int thread_count;
void* Hello(void)
{
#ifdef _OPENMP
int my_rank = omp_get_thread_num();//获取线程号
int thread_count = omp_get_num_threads();//确定当前线程组中活动线程的数量
#else
int my_rank = 0;
int thread_count = 1;
#endif
printf("Hello from thread %ld of %d\n",my_rank,thread_count);
return NULL;
}
int main(int argc,char* argv[])
{
thread_count = strtol(argv[1],NULL,10);
#pragma omp parallel num_threads(thread_count)
Hello();
return 0;
}不传惨默认电脑核数(我的电脑是12核)
计算机环境变量:OMP_NUM_THREADS
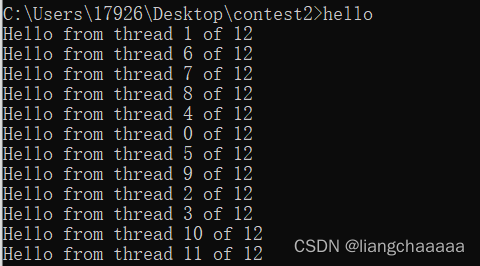
传参结果

梯形积分法
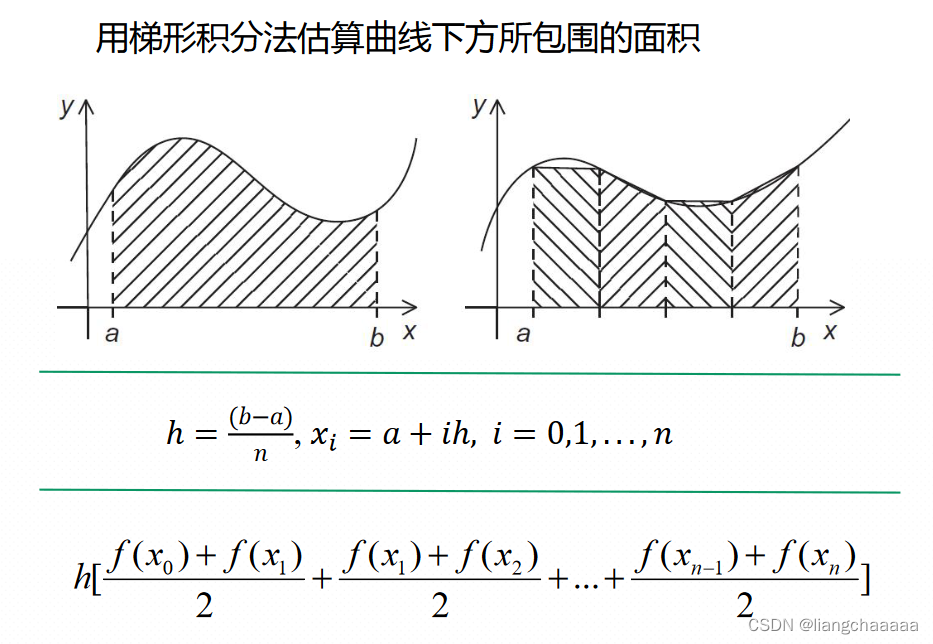
#include<stdlib.h>
#include<stdio.h>
#include<math.h>
#ifdef _OPENMP
#include<omp.h>
#endif
void work(double a,double b,int n,double *global_result)
{
#ifdef _OPENMP
int my_rank = omp_get_thread_num();//获取线程号
int thread_count = omp_get_num_threads();//确定当前线程组中活动线程的数量
#else
int my_rank = 0;
int thread_count = 1;
#endif
double h = (b-a)/n;
double my_result;
int local_n = n/thread_count;//每个线程执行多少块梯形
double local_a = a + my_rank * local_n * h;
double local_b = local_a + local_n * h;
long long i;
my_result = (sin(local_a)+sin(local_b))/2.0;
for(i=1;i<=local_n-1;i++){//这里ppt写的是i<loacl_n-1,应该是<=
double x = (double)i*h + local_a;
my_result += sin(x);
}
my_result *= h;
#pragma omp critical
{
*global_result += my_result;
}
}
int main(int argc,char* argv[])
{ int thread_count;
int n;//分割成n个梯形
double a,b;//积分区域的左右两端
double global_result = 0.0;
thread_count = strtol(argv[1],NULL,10);
printf("Please enter n,a and b\n");
scanf("%d %lf %lf",&n,&a,&b);
#pragma omp parallel num_threads(thread_count)
work(a,b,n,&global_result);
printf("result: %.6f",global_result);
return 0;
}变量作用域
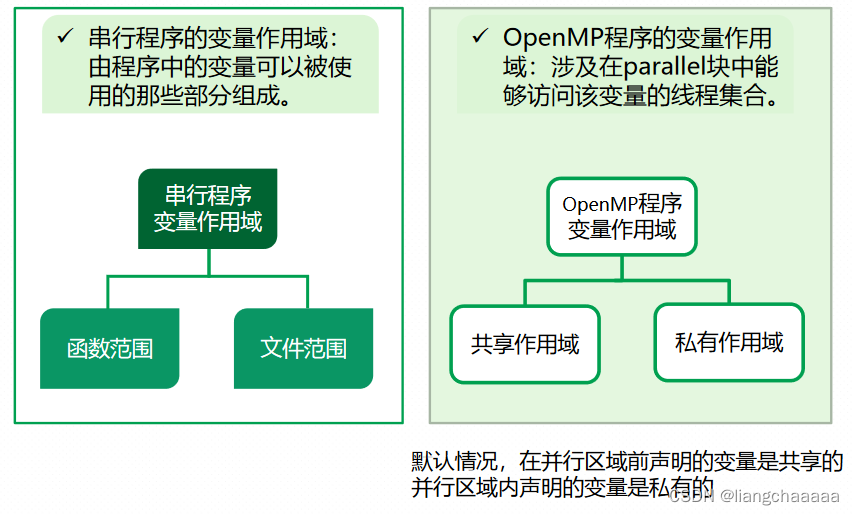
private ( list )
private将一个或多个变量声明成线程的私有变量,每个线程有自己变量私有副本,仅当前并行区域有效 。
fistprivate ( list )
对私有变量进行初始化,把串行变量值拷贝到私有变量中。
lastprivate ( list )
对私有变量的终结操作,把私有变量(最后的循环迭代)拷贝到同名串行变量中。shared ( list )
将变量声明为共享变量

上面为粗粒度锁,下面为细粒度锁
double factor = 1.0;
double sum = 0.0;
# pragma omp parallel for num_threads( th_count ) default(none) reduction( +: sum ) \
private( k, factor ) shared(n)
for ( k = 0; k < n; k ++ ) {
if ( k % 2 == 0)
factor = 1.0;
else
factor = -1.0;
sum += factor / ( 2 * k + 1 );
}
pi_approx = 4.0 * sum;default(none) 相当于在并行区域之前告诉编译器,在没有使用 shared 或 private 等指定变量共享属性的情况下,所有变量都被视为私有的。这样做是为了防止程序员忘记明确指定共享属性导致错误的结果。
归约子句
归约操作将归约操作符重复地应用于操作数序列来得到一个结果的计算
语法:reduction ( <operator> : <variable list>)

global_result = 0.0;
# pragma omp parallel num_threads (thread_count) reduction (+: global_result)
global_result += Local_trap(a,b,n);把各个线程计算的结果汇总到归约变量上
归约是通过为每个隐式任务创建每个线程的列表项的私有副本来实现的,就像使用了private子句global_result += my_result一样。
OpenMP for
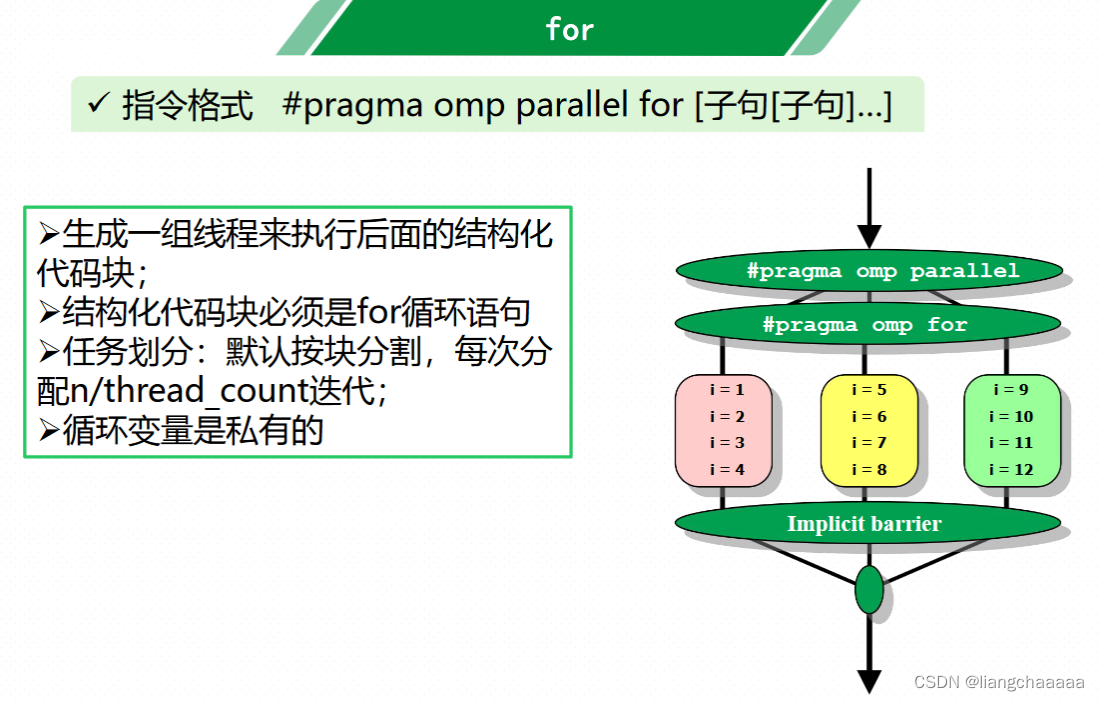
它告诉编译器,接下来的for循环将会使用并行的方式执行
使用并行的时候需要满足以下四个需求:
在循环的迭代器必须是可计算的并且在执行前就需要确定迭代的次数。
在循环的代码块中不能包含break,return,exit。
在循环的代码块中不能使用goto跳出到循环外部。
迭代器只能够被for语句中的增量表达式所修改。
嵌套循环并行化中内层循环并行和外层循环并行是不一样的
以下为2个线程为例:
1.外层:
i = 0时为一个线程,i = 1为一个线程,每个线程执行一次j = 6,7,8,9
因为是并行,所以会有i = 0和i = 1交替出现的情况,同时需要用private将j声明成线程私有变量,因为i = 0时的j和i = 1时的j不一样
2.内层:
j = 6,9为一个线程,j = 8,7为一个线程,不需要private声明,开启并行区域时,两个线程的i索引都相同,用的是同一层i下的j
 数据依赖性
数据依赖性
OpenMP编译器不检查被parallel for指令并行化的循环所包含的迭代间的依赖关系
一个或者更多个迭代结果依赖于其他迭代的循环,一般不能被正确的并行化有数据依赖关系的计算被分配到一个线程,不会影响计算结果
比如在斐波那契数列,算了前面的才能算后面的,但是parallel for会把n次迭代分配好后同时开始算,并不会等计算下标在前的数的线程算好后再算
OpenMP section and single


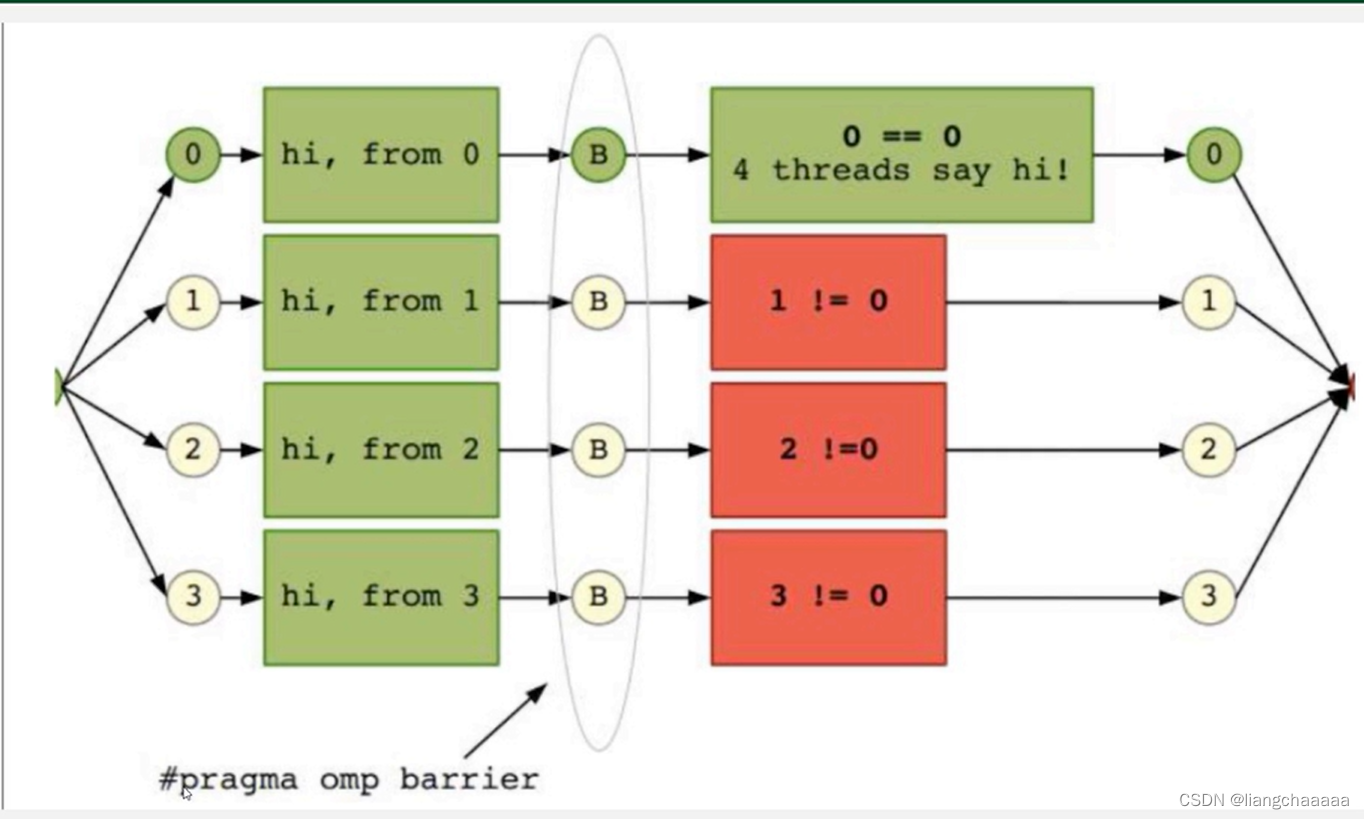
OpenMP barrier

循环调度









![[JavaWeb]SQL介绍-DDL-DML](https://img-blog.csdnimg.cn/05033827a41648daa359f62a65d01cfc.png#pic_center)

![[nlp] TF-IDF算法介绍](https://img-blog.csdnimg.cn/4e186ba8072d46ecac7be6eda9f882ba.png)