392. 判断子序列

这道题和1143最长公共字串相同
dp[i][j] 表示以下标i-1为结尾的字符串s，和以下标j-1为结尾的字符串t，相同子序列的长度为dp[i][j]。

class Solution {
    public boolean isSubsequence(String s, String t) {
    
    char[] A = s.toCharArray();
    char[] B = t.toCharArray();

    int [][] dp = new int[A.length+1][B.length+1];

    for(int i=1;i<=A.length;i++){
        for(int j=1;j<=B.length;j++){
            if(A[i-1] == B[j-1]){
                dp[i][j] = dp[i-1][j-1]+1;
            }else{
                dp[i][j] = Math.max(dp[i][j-1],dp[i-1][j]);
            }
        }
    }
    return dp[A.length][B.length] == s.length();
    }
}

方法二
双指针

class Solution {
    public boolean isSubsequence(String s, String t) {
    if(s.length() == 0){
        return true;
    }

  int i=0;
  int j =0;
  while(i<s.length() && j<t.length()){
      if(s.charAt(i)== t.charAt(j)){
          i++;
      }
      j++;
  }
  return i == s.length();
    }
}

115.不同的子序列

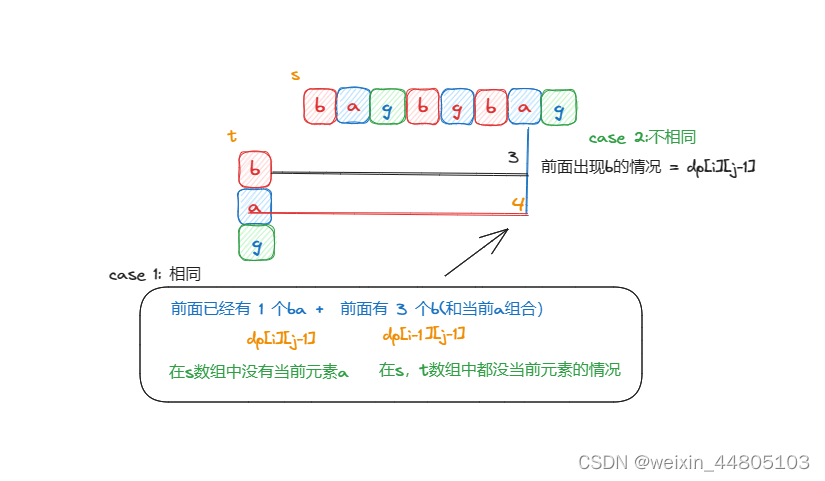
dp[i][j]：以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]。

这个把递推讲的很详细

初始化：
状态方程：
相同的情况：$dp[i][j]=dp[i-1][j-1]+dp[i][j-1]$
初始化，如果t表示空，那么在s中只有一个子集, $dp[0][j]=1$

class Solution {
    public int numDistinct(String s, String t) {
   char[] A = s.toCharArray();
    char[] B = t.toCharArray();

    int[][] dp = new int[B.length + 1][A.length + 1];
        for (int i = 0; i < A.length+ 1; i++) { // 长的那个s
            dp[0][i] = 1;
        }
        
        for (int i = 1; i <= B.length; i++) {
            for (int j = 1; j <= A.length; j++) {
                if (B[i - 1] == A[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + dp[i][j-1];
                }else{
                    dp[i][j] = dp[i ][j-1];
                }
            }
        }
        
        return dp[B.length][A.length];
    }
}