class Solution {
public:
int dp[2510];
int lengthOfLIS(vector<int>& nums) {
//dp[i]表示以nums[i]为结尾的最长子序列的长度
int n=nums.size();
for(int i=0;i<n;i++){
dp[i]=1;
}
for(int i=1;i<n;i++)
{
for(int j=0;j<i;j++)
{
if(nums[i]>nums[j])
{
dp[i]=max(dp[i],dp[j]+1);
}
}
}
int res=1;
for(int i=0;i<n;i++)
{
res=max(res,dp[i]);
}
return res;
}
};

class Solution {
public:
int dp[10005];
int findLengthOfLCIS(vector<int>& nums) {
int n=nums.size();
//dp[i]表示以nums[i]结尾的最长且连续递增的子序列的长度
for(int i=0;i<n;i++)
{
dp[i]=1;
}
int res=1;
for(int i=1;i<n;i++){
if(nums[i]>nums[i-1])
{
dp[i]=dp[i-1]+1;
}
else{
dp[i]=1;
}
res=max(res,dp[i]);
}
return res;
}
};
class Solution {
public:
int dp[1005][1005];
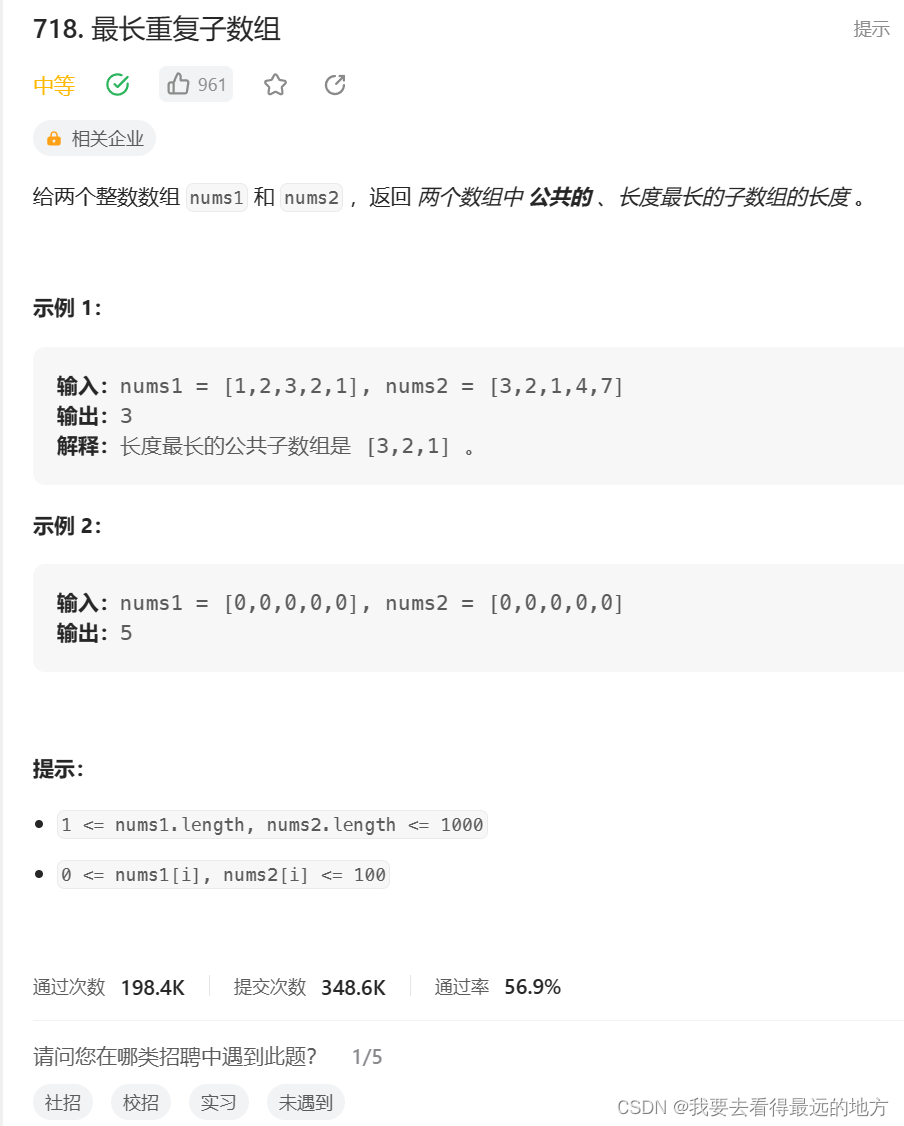
int findLength(vector<int>& nums1, vector<int>& nums2) {
int res=0;
//dp[i][j]表示以nums1[i],nums2[j]结尾的 公共的 、长度最长的子数组的长度
for(int i=1;i<=nums1.size();i++){
for(int j=1;j<=nums2.size();j++){
if(nums1[i-1]==nums2[j-1]){
dp[i][j]=dp[i-1][j-1]+1;
}
res=max(res,dp[i][j]);
}
}
return res;
}
};

class Solution {
public:
int dp[1005][1005];
int longestCommonSubsequence(string text1, string text2) {
//dp[i][j]表示以text1[i-1]和text2[j-1]结尾的最长 公共子序列 的长度
for(int i=1;i<=text1.size();i++)
{
for(int j=1;j<=text2.size();j++)
{
if(text1[i-1]==text2[j-1])
{
dp[i][j]=dp[i-1][j-1]+1;
}
else
{
dp[i][j]=max(dp[i][j-1],dp[i-1][j]);
}
}
}
return dp[text1.size()][text2.size()];
}
};

class Solution {
public:
int dp[505][505];
int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {
//dp[i][j] 表示以nums1[i-1],nums2[j-1]结尾的最长公共子序列的长度
int res=0;
for(int i=1;i<=nums1.size();i++){
for(int j=1;j<=nums2.size();j++){
if(nums1[i-1]==nums2[j-1]){
dp[i][j]=dp[i-1][j-1]+1;
}else{
dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
}
res=max(res,dp[i][j]);
}
}
return res;
}
};
class Solution {
public:
int dp[100005];
int maxSubArray(vector<int>& nums) {
int len=nums.size();
int res=-1e5;
for(int i=0;i<len;i++){
res=max(res,nums[i]);
}
//dp[i]表示以nums[i]为结尾的最大和的连续子数组
dp[0]=max(nums[0],0);
for(int i=1;i<nums.size();i++){
dp[i]=max(dp[i-1]+nums[i],nums[i]);
res=max(res,dp[i]);
}
return res;
}
};
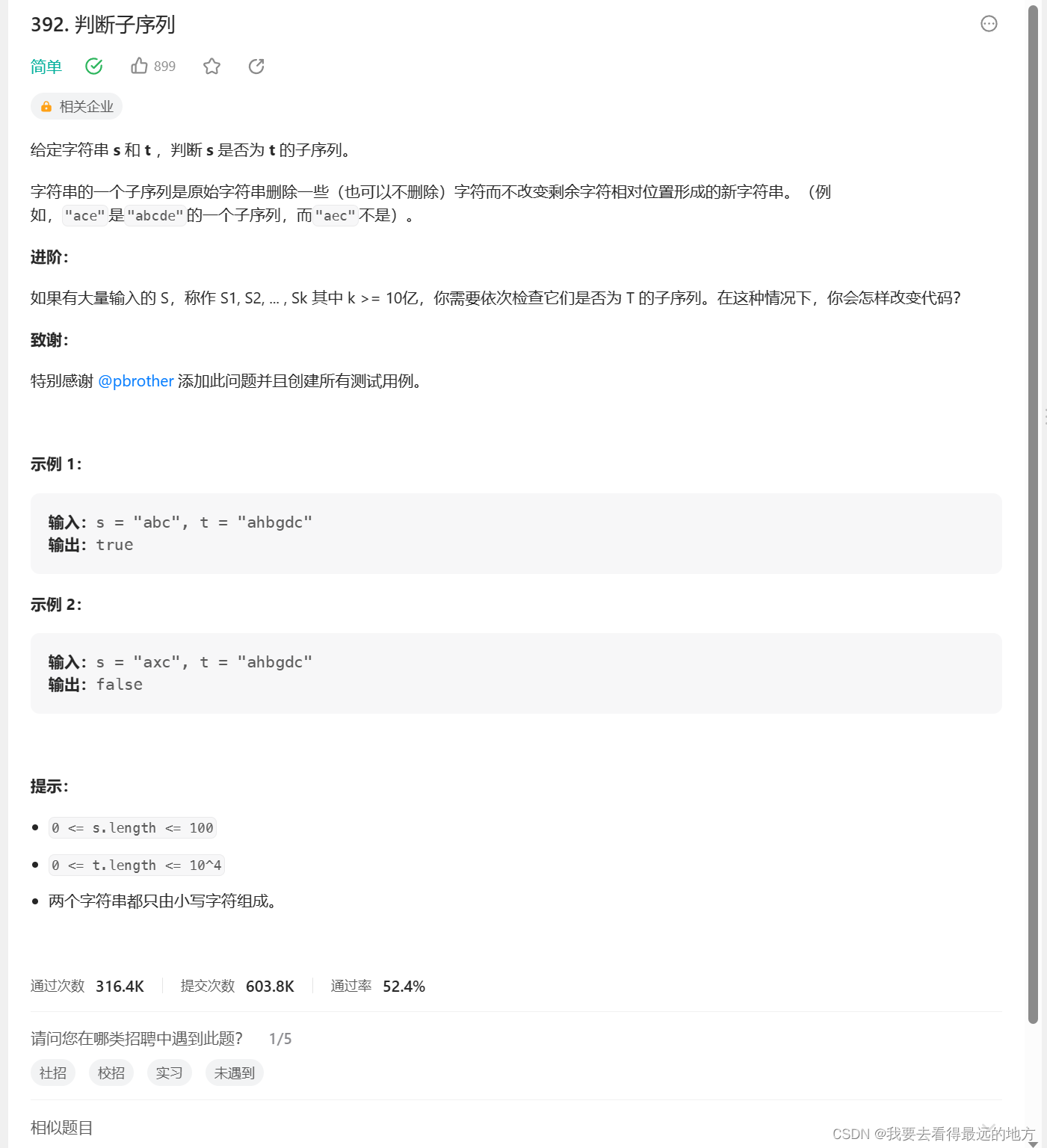
//方法一
class Solution {
public:
bool isSubsequence(string s, string t) {
int j=0;
for(int i=0;i<t.length();i++)
{
if(t[i]==s[j])
{
j++;
}
}
if(j==s.length())
{
return true;
}
else{
return false;
}
}
};
//方法二
class Solution {
public:
int dp[105][10005];
bool isSubsequence(string s, string t) {
//dp[i][j] 表示以s[i-1],t[i-1]结尾的s和t的相同子序列的长度
for(int i=1;i<=s.length();i++)
{
for(int j=1;j<=t.length();j++)
{
if(s[i-1]==t[j-1])
{
dp[i][j]=dp[i-1][j-1]+1;
}
else{
dp[i][j]=dp[i][j-1];
// 0.....i-1
// 0.....j-1
//由于s[i-1]和[j-1]是属于不同,就相当于把t[j-1]这个字符删掉了.
}
}
}
int res=dp[s.length()][t.length()];
if(res==s.length()){
return true;
}
else{
return false;
}
}
};

class Solution {
public:
unsigned long long dp[1005][1005];//注意类型
int numDistinct(string s, string t) {
//dp[i-1][j-1]表示以i-1结尾的s中有几个以j-1为结尾的t;
int sl=s.length();
int tl=t.length();
for(int i=0;i<=tl;i++)
{
dp[0][i]=0;
}
for(int i=0;i<=sl;i++)
{
dp[i][0]=1;
}
dp[0][0]=1;
for(int i=1;i<=sl;i++)
{
for(int j=1;j<=tl;j++)
{
if(s[i-1]==t[j-1]){
dp[i][j]=dp[i-1][j-1]+dp[i-1][j];
//dp[i][j-1]表示不考虑i-1
}
else{
dp[i][j]=dp[i-1][j];
}
}
}
return dp[sl][tl];
}
};
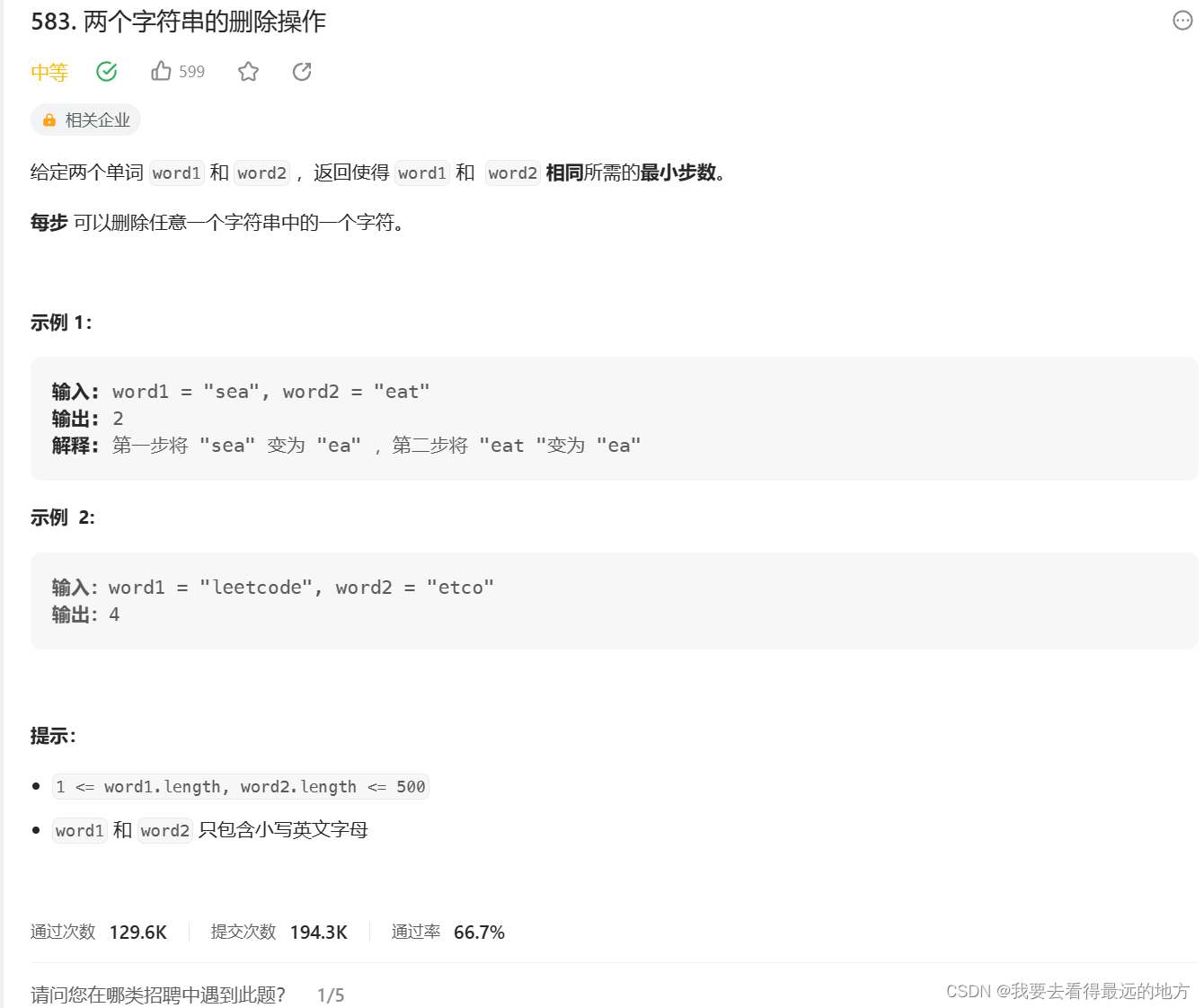
//方法一 首先求两个字符串的最长公共子序列,然后用总长度减掉最长公共子序列长度
class Solution {
public:
int dp[505][505];
int minDistance(string word1, string word2) {
//dp[i][j]表示以i-1结尾的word1,和以j-1结尾的word2的最长公共子序列
for(int i=1;i<=word1.length();i++)
{
for(int j=1;j<=word2.length();j++){
if(word1[i-1]==word2[j-1]){
dp[i][j]=dp[i-1][j-1]+1;
}
else
{
dp[i][j]=max(dp[i][j-1],dp[i-1][j]);
}
}
}
return word1.length()+word2.length()- 2*dp[word1.length()][word2.length()];
}
};
//方法二
class Solution {
public:
int dp[505][505];
int minDistance(string word1, string word2) {
//dp[i][j]表示以i-1结尾的word1,和以j-1结尾的word2相同所需的最小步数
int l1=word1.length();
int l2=word2.length();
for(int i=0;i<=l1;i++)
{
dp[i][0]=i;
}
for(int j=0;j<=l2;j++)
{
dp[0][j]=j;
}
for(int i=1;i<=l1;i++){
for(int j=1;j<=l2;j++){
if(word1[i-1]==word2[j-1])
{
dp[i][j]=dp[i-1][j-1];
//两者相同不删
}
else{
dp[i][j]=min(dp[i-1][j]+1,min(dp[i][j-1]+1,dp[i-1][j-1]+2));
//dp[i-1][j]删掉i-1;
//dp[i][j-1]删掉j-1;
//dp[i-1][j-1]两者都删掉
}
}
}
return dp[l1][l2];
}
};
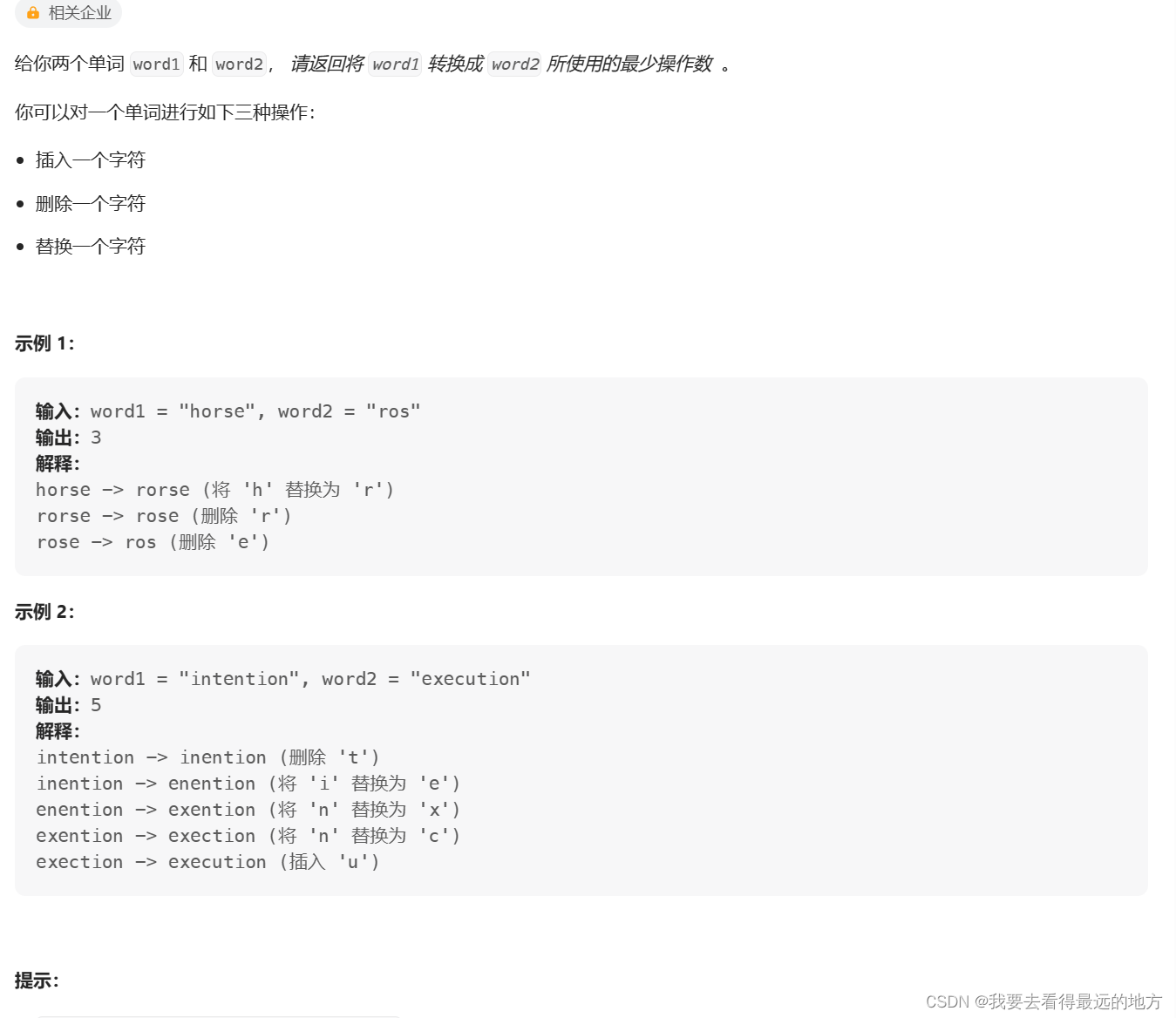
class Solution {
public:
int dp[505][505];
int minDistance(string word1, string word2) {
//dp[i][j]表示以word1[i-1]结尾的和以word2[j-1]结尾的,1变为2的最小操作数
int l1=word1.length();
int l2=word2.length();
for(int i=0;i<=l1;i++)
{
dp[i][0]=i;
}
for(int j=0;j<=l2;j++)
{
dp[0][j]=j;
}
for(int i=1;i<=l1;i++){
for(int j=1;j<=l2;j++){
if(word1[i-1]==word2[j-1]){
dp[i][j]=dp[i-1][j-1];
}
else{
dp[i][j]=min(dp[i-1][j]+1,min(dp[i][j-1]+1,dp[i-1][j-1]+1));
//dp[i-1][j]+1表示删除word1[i-1];
//dp[i][j-1]+1表示删除word2[j-1]相当于在word1中添加一个元素
//dp[i-1][j-1]+1替换将word1[i-1]替换为word2[j-1]
}
}
}
return dp[l1][l2];
}
};

class Solution {
public:
bool dp[1005][1005];
int countSubstrings(string s) {
//dp[i][j]表示s[i]...s[j]是不是回文子串
int res=0;
for(int i=s.size()-1;i>=0;i--)
{
for(int j=i;j<s.size();j++)
{
if(s[i]==s[j])
{
if(j-i<=1)
{
dp[i][j]=true;
res++;
}
else{
if(dp[i+1][j-1]==true)
{
dp[i][j]=true;
res++;
}
}
}
}
}
return res;
}
};

class Solution {
public:
int dp[1005][1005];
int longestPalindromeSubseq(string s) {
//dp[i][j]表示s[i]....s[j]最长回文子序列的长度
for(int i=0;i<s.size();i++){
dp[i][i]=1;
}
for(int i=s.size()-1;i>=0;i--){
for(int j=i+1;j<s.size();j++){
if(s[i]==s[j]){
dp[i][j]=dp[i+1][j-1]+2;
}
else{
dp[i][j]=max(dp[i+1][j],dp[i][j-1]);
//dp[i+1][j],不考虑s[i]
//dp[i][j-1],不考虑s[j-1]
}
}
}
return dp[0][s.size()-1];
}
};