💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
文献来源:

本文讲解一种数据驱动的信号去噪方法,该方法利用变分模态分解(VMD)算法和Cramer Von Misses(CVM)统计。与传统的经验模态分解(EMD)相比,VMD具有优越的数学和理论框架,使其对噪声和模态混合具有鲁棒性。 VMD的这些理想特性是通过将大部分噪声分离成几种最终模式来实现的,而大部分信号内容则分布在早期模式中。为了利用这种表示进行降噪,我们建议估计来自主要噪声模式的噪声分布,然后使用它来检测和抑制来自其余模式的噪声。该方法首先利用统计距离的CVM度量来选择主要噪声模式。接下来,在其余模式上局部使用 CVM 统计量来测试这些模式与估计噪声分布的拟合程度;与噪声分布产生更接近拟合的模式被拒绝(设置为零)。大量的实验证明了所提出的方法在信号去噪方面优于现有技术,并强调了其在噪声分布未知的实际应用中的实用性。
由于采集系统(例如录音系统、激光雷达系统、脑电图和心电图采集系统等)的各种物理限制,来自各种实际应用的信号会受到不必要的噪声的影响。因此,为了避免基于这些噪声信号做出任何错误的决定,有必要事先消除不需要的噪音。在这方面,通常假设时间序列数据中的噪声遵循加性白高斯噪声(wGn)模型。对于广义稳态信号,即具有完全已知的不变统计量的信号,使用Weiner滤波器,去除加性wGn的问题得到了最佳解决。但是,由于以下原因,这种方法在实际环境中可能不够。首先,大多数现实生活中的信号是非平稳的,因为它们的属性(统计数据)随时间变化。其次,假设的wGn模型可能并不总是用于表征时间序列数据中的噪声,例如EEG / ECG信号。因此,需要能够解释信号的非平稳性和噪声的非高斯性的更先进的技术。
离散小波变换(DWT)是一种处理非平稳信号的多尺度方法,其特性是信号奇异点在其系数内稀疏分布。另一方面,噪声系数具有较低的振幅和均匀的扩散[1]。这允许使用合适的阈值(例如,通用阈值[2])或统计收缩函数(例如[3],[4])来区分信号和噪声系数。这些方法的基础建立在关于(真实)信号和噪声的(分布)模型的先前假设之上。在这方面,数据采集和通信系统引起的随机噪声通常使用加性wGn模型进行建模,但这并不能完全考虑采集过程中导致噪声的因素。然而,由于时间序列数据中通常发现的信息具有任意性,因此指定信号模型具有挑战性。此外,先前模型的规范限制了这些方法在现实世界信号中的功效。
这个问题已经在[5]中提出的框架内得到了部分解决,该框架将DWT与拟合优度(GoF)检验相结合。此后,这种方法被称为DWT-GoF方法。值得一提的是,DWT-GoF方法只需要先验噪声模型。例如,在这里,噪声被方便地建模为零均值加性wGn。DWT保留了噪声的高斯性,有助于在多个小波尺度上检测wGn。这基本上需要检测和抑制拟合高斯分布的小波系数以进行去噪。此后,DWT-GoF方法[5]通过在多尺度系数上估计高斯分布的GoF来抑制来自DWT尺度的噪声。DWT-GoF方法的改进版本在[6],[7]中提出了,该方法采用GoF测试以及双树复小波变换(DTCWT),在续集中称为DT-GOF-NeighFilt方法。DT-GOF-NeighFilt方法的主要特点是结合一种新的邻域滤波技术,以最大限度地减少信号细节的损失,同时抑制噪声。除GoF检验外,其他假设检验工具,如错误发现率(FDR),贝叶斯局部错误发现率(BLFDR)也与小波变换结合使用,用于信号去噪[8]。
多尺度去噪的另一种途径涉及数据驱动的分解技术。例如,经验模式分解(EMD)[9]采用数据驱动的方法从信号中提取主要振荡模式。由于EMD能够将信号扩展为其固有的固有模式函数(IMF),EMD被认为非常适合处理实践中通常遇到的非平稳信号。当用于去噪时,EMD旨在检测代表(振荡)信号部分的IMF,并抑制与非振荡噪声相对应的IMF。小波启发的区间阈值函数用于检测来自噪声IMF的振荡信号部分[10]。具体来说,基于EMD的间隔阈值(EMD-IT)[10]旨在检测由两个连续的过零分开的振荡。这是通过将区间的极值与导致保留或拒绝整个区间的阈值进行比较来实现的。
[11]中的工作没有执行阈值,而是使用统计工具来检测相关(信号)模式,以便对去噪信号进行部分重建。然而,由于EMD的模式混合(即单个IMF中多个IMF的表现)特性及其对噪声和采样的敏感性,这些去噪方法可能会导致性能欠佳。从本质上讲,EMD框架内的上述缺点会导致噪声泄漏到一些信号模式中,从而导致噪声抑制,从而导致次优去噪。EMD缺乏数学基础限制了在其框架内纠正这些问题的机会。
最近提出的变分模态分解(VMD)基于变分问题的优化,以获得固定数量的带限IMF(BLIMF)的集合[12]。由于其良好的数学基础,VMD成功地避免了模式混合,并且与EMD不同,它对噪声和采样具有鲁棒性[12],[13]。从去噪的角度来看,VMD的一个非常重要的特性是它能够将所需信号分离成几个初始BLIMF,而噪声主要隐藏在几个最终BLIMF中。因此,通过抑制带噪声的模式,可以通过部分重建获得对真实信号的良好估计。
文献综述表明,现有的基于VMD的去噪方法通过将单个BLIMF的概率分布函数(PDF)与噪声信号的PDF进行比较来选择相关的信号模式。这是有根据的,因为分布函数通常反映噪声数据中存在的信号。BLIMF中存在的信号的估计可以通过测量其PDF与噪声信号的接近程度来获得,例如,通过使用欧几里得距离[14],巴塔查里亚距离[15]等。其中,统计上接近噪声信号的模式被选为相关(信号)模式,而大相径庭的模式则被排除为噪声。有关各种统计距离对估计相关模式的有效性的详细研究,请参阅感兴趣的读者[16]。此外,[17]中的方法使用去趋势波动分析(DFA)(最初在EMD-DFA方法[11]中与EMD一起使用)选择相关模式,该模式通过观察缺乏趋势来估计数据的随机性。这种方法,以下简称VMD-DFA [17],抑制噪声BLIMF,并根据其余模式重建去噪信号。
这些基于VMD的方法的问题在于(a)所选(低频)信号模式中存在噪声,导致去噪信号中出现明显伪影,以及(b)作为拒绝模式的一部分,高频信号细节丢失,导致不合格的去噪。这个问题没有得到研究人员的太多关注,这可能是因为与EMD/MEMD广泛使用的间隔阈值技术[10],[18],[19]由于噪声功率在BLIMF之间的任意分布,不能直接适用于VMD / MVMD模式。另一方面,为VMD的BLIMF设计类似小波的统计阈值技术需要事先了解噪声(和/或信号)的分布。这是具有挑战性的,因为VMD由于其非线性,将已知的噪声分布(例如,高斯分布)转换为未知的噪声分布。因此,阻碍了开发用于信号估计的统计方法的可能性。
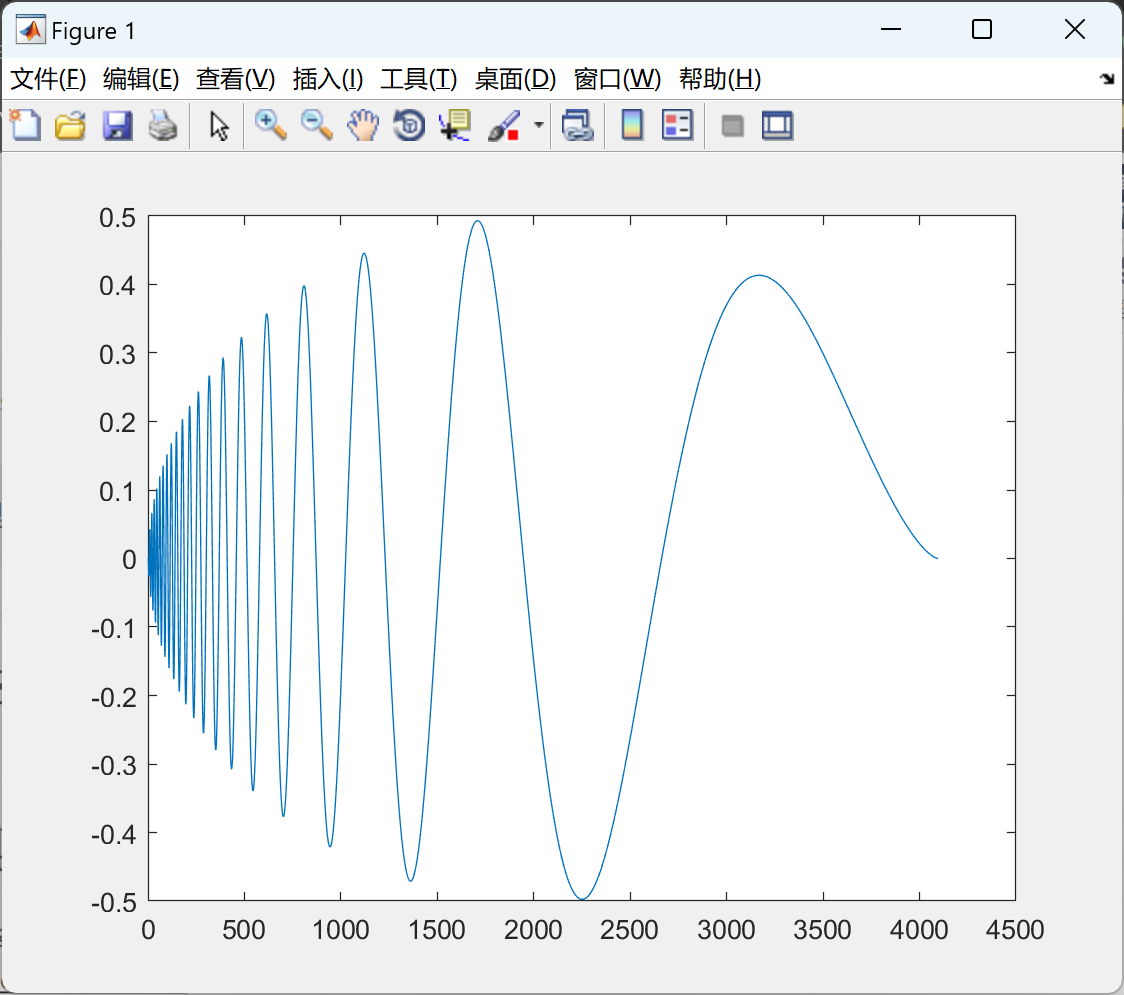
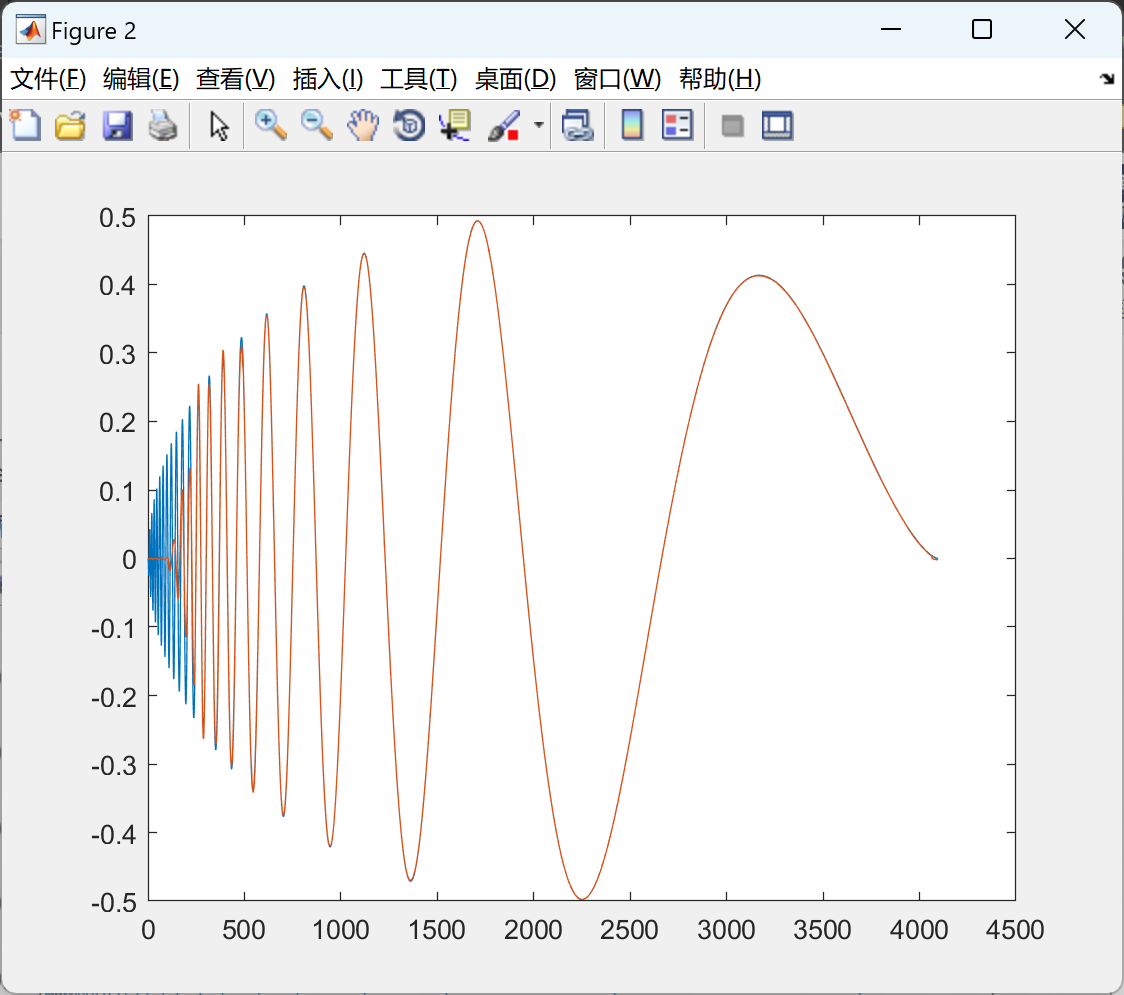
📚2 运行结果
命令框输入任意一种,以4为例。

🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。