4 李群与李代数

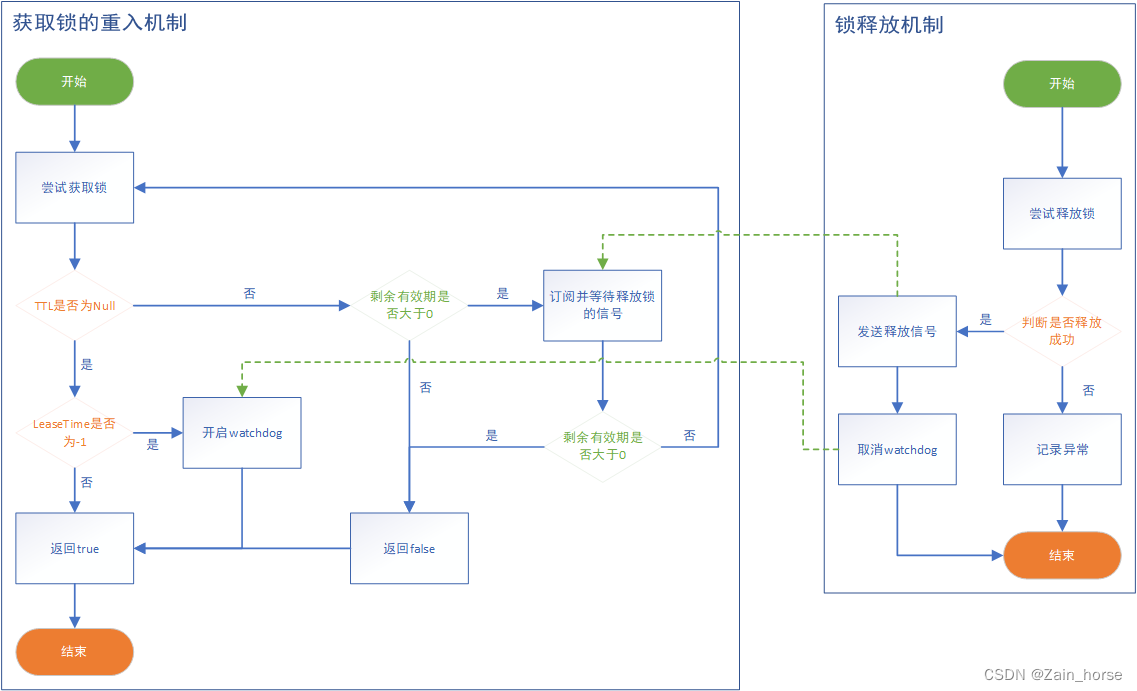
为了解决什么样的相机位姿最符合当前观测数据的问题，可以构建出一个优化问题来求解最优的R和t。以达到误差最小。但是旋转矩阵自身是带有约束的（正交且行列式为1），这会引入额外的约束，导致优化变得困难。通过李群——李代数这种关系，希望把位姿估计的问题变为无约束的优化问题。

4.1 李群与李代数基础

4.1.1 群

群(Group)是一种集合加上一种运算的代数结构。把集合记作A，运算记作$\cdot$ ,那么群可以记作G = ( A , ⋅ )。群要求这个运算满足如下条件：

• 封闭性
• 结合律
• 幺元
• 逆

李群是指具有连续(光滑)性质的群。SO(3)和SE(3)都是李群。

4.1.2 李代数的引出

4.1.3 李代数的定义

每个李群都有与之对应的李代数，李代数描述了李群的局部性质。
李代数由一个集合V、一个数域F和一个二元运算[ , ]（又称李括号）组成。如果它们满足以下几条性质，则称( V , F , [ , ] )为一个李代数,记作g。

• 封闭性
• 双线性
• 自反性（自己与自己的运算为零）
• 雅可比等价

4.2 指数与对数映射

4.3 李代数求导与扰动模型

引入李代数的一大动机就是方便求导优化。

5 相机与图像

5.1 相机模型

5.1.1 针孔相机模型

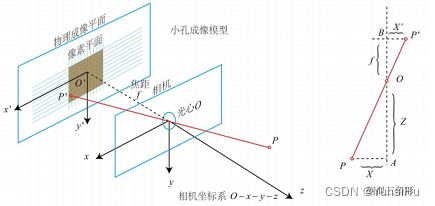
对内参、外参是怎么来的，做了推导。

5.1.2 畸变

畸变包含两种：径向畸变和切向畸变。
径向畸变：由透镜形状引起，主要包括桶形畸变和枕形畸变。可以看成坐标点沿着长度方向发生了变化，也就是其距离原点的长度发生了变化。
切向畸变：由透镜和成像平面不严格平行引起。可以看成坐标点沿着切线方向发生了变，也就是水平夹角发生了变化。

5.1.3 双目相机

基线：两个相机的光圈中心都位于x轴上，它们的距离称为双目相机的基线。
视差：左右图的横坐标之差。视差越大，距离越近。

5.1.4 RGB-D相机

按原理可以分为红外结构光型和飞行时间法（ToF）型。

6 非线性优化