931. 下降路径最小和

给你一个 n x n 的 方形 整数数组 matrix ，请你找出并返回通过 matrix 的下降路径 的 最小和 。

下降路径可以从第一行中的任何元素开始，并从每一行中选择一个元素。在下一行选择的元素和当前行所选元素最多相隔一列（即位于正下方或者沿对角线向左或者向右的第一个元素）。具体来说，位置(row, col) 的下一个元素应当是 (row + 1, col - 1)、(row + 1, col) 或者 (row + 1, col + 1) 。

示例 1：

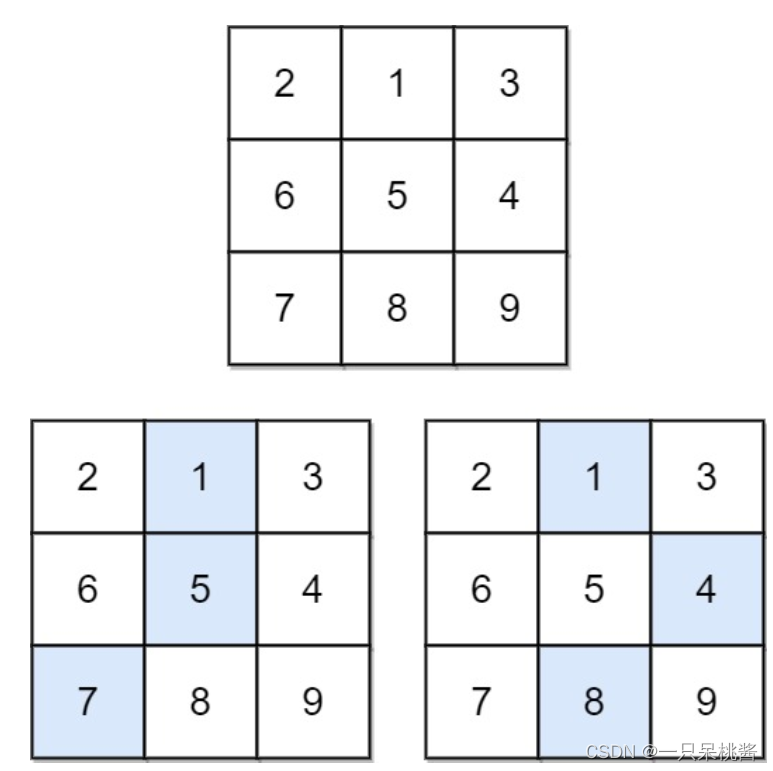
输入：matrix = [[2,1,3],[6,5,4],[7,8,9]]
输出：13
解释：如图所示，为和最小的两条下降路径

示例 2：

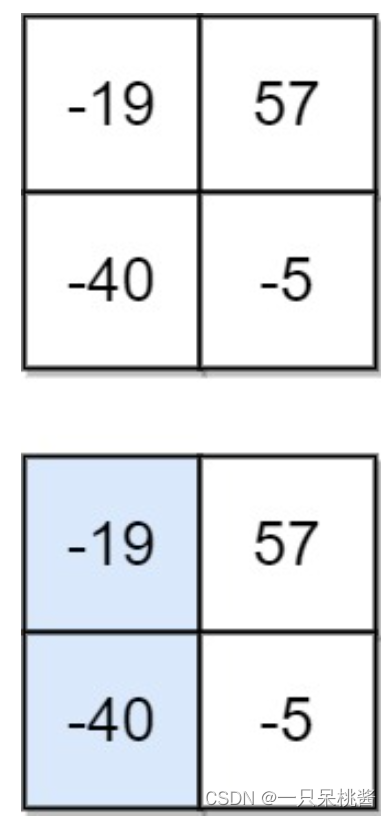
输入：matrix = [[-19,57],[-40,-5]]
输出：-59
解释：如图所示，为和最小的下降路径
 

提示：

n == matrix.length == matrix[i].length
1 <= n <= 100
-100 <= matrix[i][j] <= 100

dp[i][j]=min(dp[i-1][j-1],dp[i-1][j],dp[i-1][j+1])

class Solution {
    public int minFallingPathSum(int[][] matrix) {
       //d[i][j]=min(d[i-1][j-1],d[i-1][j],d[i-1][j+1])+matrix[i][j]
        int ans=Integer.MAX_VALUE;
        int n=matrix.length;
        int[][] dp=new int[n][n];
        if(n==1) return matrix[0][0];
        for(int i=0;i<n;i++) {
            dp[0][i] = matrix[0][i];
        }
        for(int i=1;i<n;i++){
            for(int j=0;j<n;j++){
                if(j==0){
                    dp[i][j]=Math.min(dp[i-1][j],dp[i-1][j+1]);
                }else if(j==n-1){
                    dp[i][j]=Math.min(dp[i-1][j-1],dp[i-1][j]);
                }else{
                    dp[i][j]=Math.min(Math.min(dp[i-1][j-1],dp[i-1][j]),dp[i-1][j+1]);
                }
                dp[i][j]+=matrix[i][j];
                if(i==n-1){
                    ans=Math.min(ans,dp[i][j]);
                }
            }
        }
        return ans;
    }
}

979. 在二叉树中分配硬币

给定一个有 N 个结点的二叉树的根结点 root，树中的每个结点上都对应有 node.val 枚硬币，并且总共有 N 枚硬币。

在一次移动中，我们可以选择两个相邻的结点，然后将一枚硬币从其中一个结点移动到另一个结点。(移动可以是从父结点到子结点，或者从子结点移动到父结点)。

返回使每个结点上只有一枚硬币所需的移动次数。

示例 1：

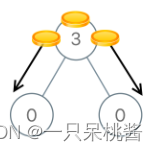
输入：[3,0,0]
输出：2
解释：从树的根结点开始，我们将一枚硬币移到它的左子结点上，一枚硬币移到它的右子结点上。

示例 2：

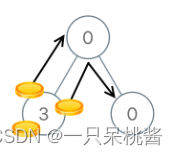
输入：[0,3,0]
输出：3
解释：从根结点的左子结点开始，我们将两枚硬币移到根结点上 [移动两次]。然后，我们把一枚硬币从根结点移到右子结点上。

示例 3：

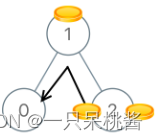
输入：[1,0,2]
输出：2

示例 4：

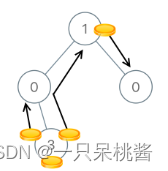
输入：[1,0,0,null,3]
输出：4
 
提示：

1<= N <= 100
0 <= node.val <= N

581. 最短无序连续子数组

给你一个整数数组 nums ，你需要找出一个 连续子数组 ，如果对这个子数组进行升序排序，那么整个数组都会变为升序排序。

请你找出符合题意的 最短 子数组，并输出它的长度。

示例 1：

输入：nums = [2,6,4,8,10,9,15]
输出：5
解释：你只需要对 [6, 4, 8, 10, 9] 进行升序排序，那么整个表都会变为升序排序。

示例 2：

输入：nums = [1,2,3,4]
输出：0

示例 3：

输入：nums = [1]
输出：0
 
提示：

1 <= nums.length <= 104
-105 <= nums[i] <= 105
 
进阶：你可以设计一个时间复杂度为 O(n) 的解决方案吗？

方法一：时间复杂度O(n^2)

public static int findUnsortedSubarray(int[] nums) {
        //从左侧开始遍历找第一个存在右侧元素大于它的，它便为升序排序最左侧元素
        //再从右侧开始遍历找第一个存在左侧元素小于它的，它便为升序排序最右侧元素
        int n=nums.length;
        int indexLeft=-1,indexRight=n;
        for(int i=0;i<n-1;i++){
            for(int j=i+1;j<n;j++){
                if(nums[i]>nums[j]){
                    indexLeft=i;
                    break;
                }
            }
            if(indexLeft!=-1){
                break;
            }
        }
        //原序列已经是个升序序列
        if(indexLeft==-1){
            return 0;
        }
        for(int i=n-1;i>0;i--){
            for(int j=i-1;j>=0;j--){
                if(nums[i]<nums[j]){
                    indexRight=i;
                    break;
                }
            }
            if(indexRight!=n){
                break;
            }
        }
        return indexRight-indexLeft+1;
    }

方法二：时间复杂度O(n)

我提供一个我的理解（有点贪心的感觉）：

首先，我们希望这个数组是单调递增的（不是严格单调递增，相邻可以相等）
从左往右，一开始max是第一个数。如果数组符合要求，那么遍历的每一个数都只会相等或者越来越大，也就是我们只会不停地更新max的值。但是，一旦碰到一个小于max的数，就说明这个数字的位置不对，这个数字一定是在我们最终要重新sort的subarray里的，并且是右边界（因为我们在不断向右探索）。
从右往左同理，只是大小关系反一反，我们能找到需要重新sort的subarray的左边界。

这样就找到答案了。

法二的理解

从左往右遍历，遍历到i，max记录的是从0到i最大的数，如果第i个位置比max小，证明第i位置元素处在一个不正确的位置(因为它前面有个比它大的数)，记录下标high。

从右往左遍历，遍历到i，min记录的是从末尾元素到i元素最小的数，如果第i位置元素比min大了，证明第i位置元素也处在一个不正确的位置(因为它后面有比它小的数)，记录下标low。

计算两个不正确的位置low和high之间的距离。

public static int findUnsortedSubarray(int[] nums) {
        //单调栈，或者也可以不用单调栈，直接用两个数max和min去维护
        int n=nums.length;
        int indexLeft=-1,indexRight=n;
        Deque<Integer> deque=new ArrayDeque<>();
        deque.addFirst(0);
        for(int i=1;i<n;i++){
            if(!deque.isEmpty()&&nums[i]>nums[deque.getLast()]) deque.addLast(i);
            if(!deque.isEmpty()&&nums[i]<nums[deque.getLast()]){
                indexRight=i;
            }
        }
        deque.clear();
        deque.addFirst(n-1);
        for(int i=n-2;i>=0;i--){
            if(!deque.isEmpty()&&nums[i]<nums[deque.getLast()]) deque.addLast(i);
            if(!deque.isEmpty()&&nums[i]>nums[deque.getLast()]){
                indexLeft=i;
            }
        }
        if(indexLeft==-1||indexRight==n) return 0;
        return indexRight-indexLeft+1;
    }

2208. 将数组和减半的最少操作次数

给你一个正整数数组 nums 。每一次操作中，你可以从 nums 中选择 任意 一个数并将它减小到 恰好
一半。（注意，在后续操作中你可以对减半过的数继续执行操作）

请你返回将 nums 数组和 至少 减少一半的 最少 操作数。

示例 1：

输入：nums = [5,19,8,1]
输出：3
解释：初始 nums 的和为 5 + 19 + 8 + 1 = 33 。
以下是将数组和减少至少一半的一种方法：
选择数字 19 并减小为 9.5 。
选择数字 9.5 并减小为 4.75 。
选择数字 8 并减小为 4 。
最终数组为 [5, 4.75, 4, 1] ，和为 5 + 4.75 + 4 + 1 = 14.75 。
nums 的和减小了 33 - 14.75 = 18.25 ，减小的部分超过了初始数组和的一半，18.25 >= 33/2 = 16.5 。
我们需要 3 个操作实现题目要求，所以返回 3 。
可以证明，无法通过少于 3 个操作使数组和减少至少一半。

示例 2：

输入：nums = [3,8,20]
输出：3
解释：初始 nums 的和为 3 + 8 + 20 = 31 。
以下是将数组和减少至少一半的一种方法：
选择数字 20 并减小为 10 。
选择数字 10 并减小为 5 。
选择数字 3 并减小为 1.5 。
最终数组为 [1.5, 8, 5] ，和为 1.5 + 8 + 5 = 14.5 。
nums 的和减小了 31 - 14.5 = 16.5 ，减小的部分超过了初始数组和的一半， 16.5 >= 31/2 = 16.5 。
我们需要 3 个操作实现题目要求，所以返回 3 。
可以证明，无法通过少于 3 个操作使数组和减少至少一半。
 
提示：

1 <= nums.length <= 105
1 <= nums[i] <= 107

采用java中自带的接口优先队列：PriorityQueue,其内部是默认小根堆存储的，可以根据需求更改成大根堆

class Solution {
    public int halveArray(int[] nums) {
        int res = 0;
        double sum = 0, subNum = 0;
        PriorityQueue<Double> priorityQueue = new PriorityQueue<>(Collections.reverseOrder());  //默认小根堆，本题需要使用的是大根堆
        for (int num : nums) {
            sum += num;
            priorityQueue.offer(num * 1.0);
        }
        sum = sum / 2.0;
        while(subNum<sum){
            double n=priorityQueue.poll();
            subNum+=n/2.0;
            priorityQueue.offer(n/2.0);
            res++;
        }
        return res;
    }
}

141. 环形链表

给你一个链表的头节点 head ，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。

如果链表中存在环 ，则返回 true 。 否则，返回 false 。

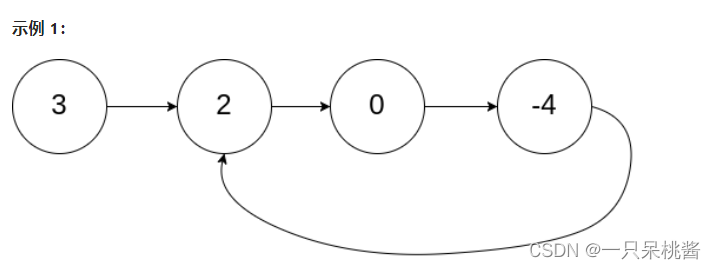
输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。

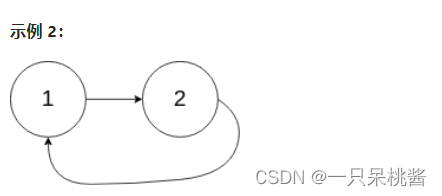
输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。

输入：head = [1], pos = -1
输出：false
解释：链表中没有环。

提示：

链表中节点的数目范围是 [0, 104]
-105 <= Node.val <= 105
pos 为 -1 或者链表中的一个 有效索引 。

法一：简单但是耗费内存，内存为O(n)

public boolean hasCycle(ListNode head) {
        //断链法
        List<ListNode> list=new ArrayList<>();
        ListNode node=head,nodeNext=null;
        while(node!=null){
            nodeNext=node.next;
            node.next=null;
            if(list.contains(node)) {
                return true;
            }
            list.add(node);
            node=nodeNext;
        }
        return false;
    }

法二：快慢指针法，经典解决链表中有环的问题

public boolean hasCycle(ListNode head) {
        //追赶法--->快慢指针法，两个指针都在环里面的时候相差一个环那么多的时候一定会相遇
        //并且快指针比慢指针每次多走一步，所以一定会相遇
        ListNode fast=head,slow=head;
        while(fast!=null&&fast.next!=null){  //不用管slow，fast永远在它前面保驾护航
            fast=fast.next.next;  //兔子走两步
            slow=slow.next;       //乌龟走一步
            if(fast==slow) return true;  //相遇
        }
        return false;    //没有环
    }