系列文章目录

文章目录

系列文章目录
前言
priority_queue的介绍
priority_queue的使用
容器适配器
- 什么是容器适配器
- STL标准库中stack和queue的底层结构
总结

前言

priority_queue是容器适配器，底层封装了STL容器。

priority_queue的介绍

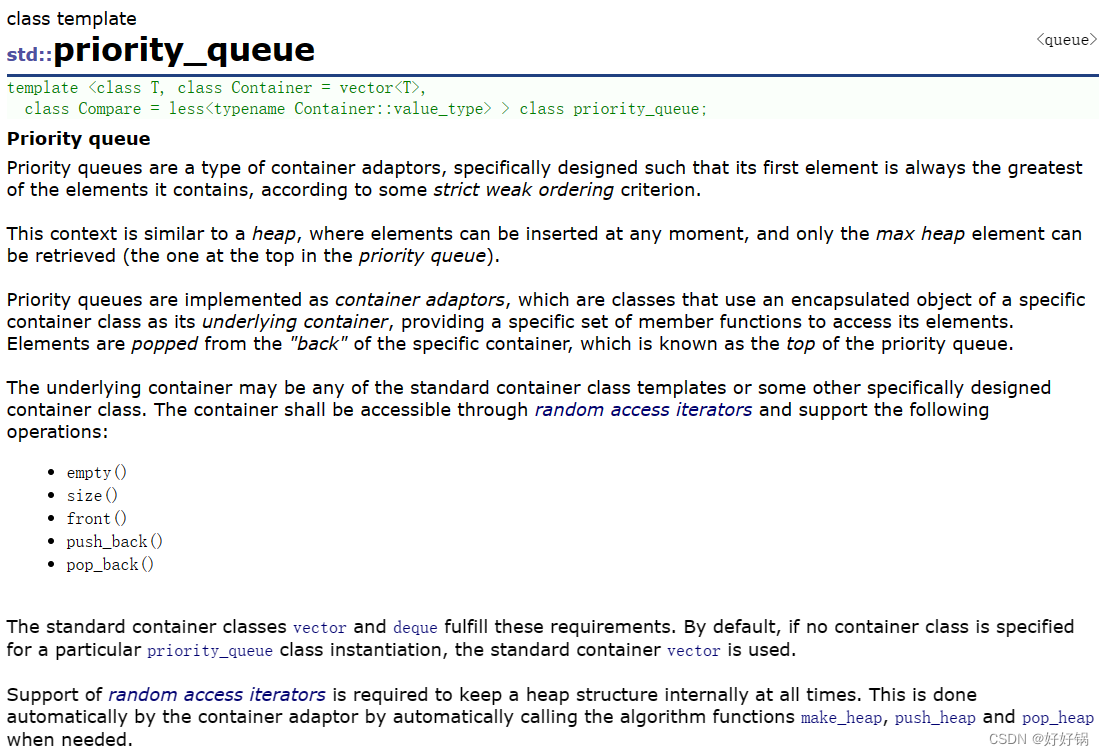
priority_queue文档介绍

优先队列是一种容器适配器，根据严格的弱排序标准，它的第一个元素总是它所包含的元素中最大的。
此上下文类似于堆，在堆中可以随时插入元素，并且只能检索最大堆元素(优先队列中位于顶部的元素)。
优先队列被实现为容器适配器，容器适配器即将特定容器类封装作为其底层容器类，queue提供一组特定的成员函数来访问其元素。元素从特定容器的“尾部”弹出，其称为优先队列的顶部。
底层容器可以是任何标准容器类模板，也可以是其他特定设计的容器类。容器应该可以通过随机访问迭代器访问，并支持以下操作：
empty()：检测容器是否为空
size()：返回容器中有效元素个数
front()：返回容器中第一个元素的引用
push_back()：在容器尾部插入元素
pop_back()：删除容器尾部元素
标准容器类vector和deque满足这些需求。默认情况下，如果没有为特定的priority_queue类实例化指定容器类，则使用vector。
需要支持随机访问迭代器，以便始终在内部保持堆结构。容器适配器通过在需要时自动调用算法函数make_heap、push_heap和pop_heap来自动完成此操作。

priority_queue的使用

在这里插入图片描述

函数声明	接口说明
priority_queue()/priority_queue(first, last)	构造一个空的优先级队列
empty( )	检测优先级队列是否为空，是返回true，否则返回false
top( )	返回优先级队列中最大(最小元素)，即堆顶元素
push(x)	在优先级队列中插入元素x
pop()	删除优先级队列中最大(最小)元素，即堆顶元素

优先级队列默认使用vector作为其底层存储数据的容器，在vector上又使用了堆算法将vector中元素构造成堆的结构，因此priority_queue就是堆，所有需要用到堆的位置，都可以考虑使用priority_queue。注意：默认情况下priority_queue是大堆。

#include <vector>
#include <queue>
#include <functional> // greater算法的头文件
void TestPriorityQueue()
{
	// 默认情况下，创建的是大堆，其底层按照小于号比较
	vector<int> v{ 3,2,7,6,0,4,1,9,8,5 };
	priority_queue<int> q1;
	for (auto& e : v)
		q1.push(e);
	cout << q1.top() << endl;
	// 如果要创建小堆，将第三个模板参数换成greater比较方式
	priority_queue<int, vector<int>, greater<int>> q2(v.begin(), v.end());
	cout << q2.top() << endl;
}