7.29
- Fibonacci数列
- 题目
- 解析
- 代码
- 合法括号序列判断
- 题目
- 题解
- 代码
- 两种排序方法
- 题目:
- 题解
- 代码
Fibonacci数列
题目
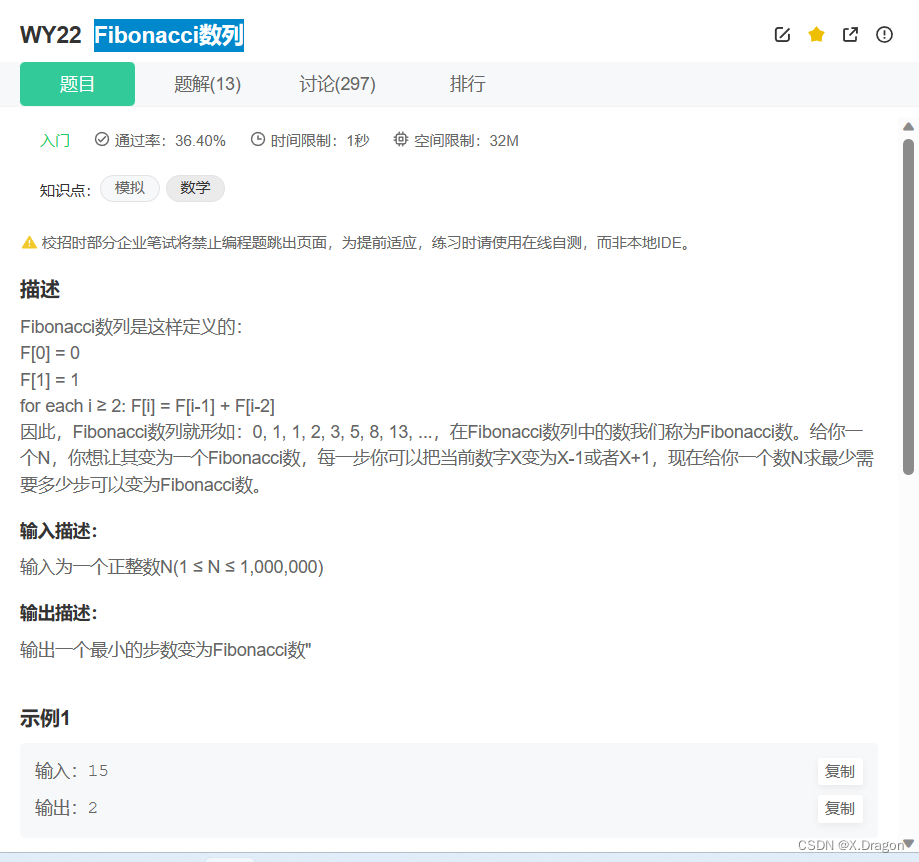
题目链接: 点击跳转
解析
- 【题目解析】:
本题是对于Fibonacci数列的一个考察,Fibonacci数列的性质是第一项和第二项都为1,后面的项形成递归:
F(n) = F(n - 1) + F(n - 2)。 - 【解题思路】:
本题可以通过先找到距离N最近的两个Fibonacci数,这两个数分别取自距离N的最近的左边一个数L和右边一个数R,然后通过min(N - L, R - N)找到最小步数。
代码
#include <iostream>
using namespace std;
int main()
{
int N,l=0,r=0,F=0,F0=0,F1=1;
cin>>N;
while (true)
{
F=F0+F1;
F0=F1;
F1=F;
if(F<N)
{
l=N-F;
}
else
{
r=F-N;
break;
}
}
cout<<min(l,r)<<endl;
}
// 64 位输出请用 printf("%lld")
合法括号序列判断
题目
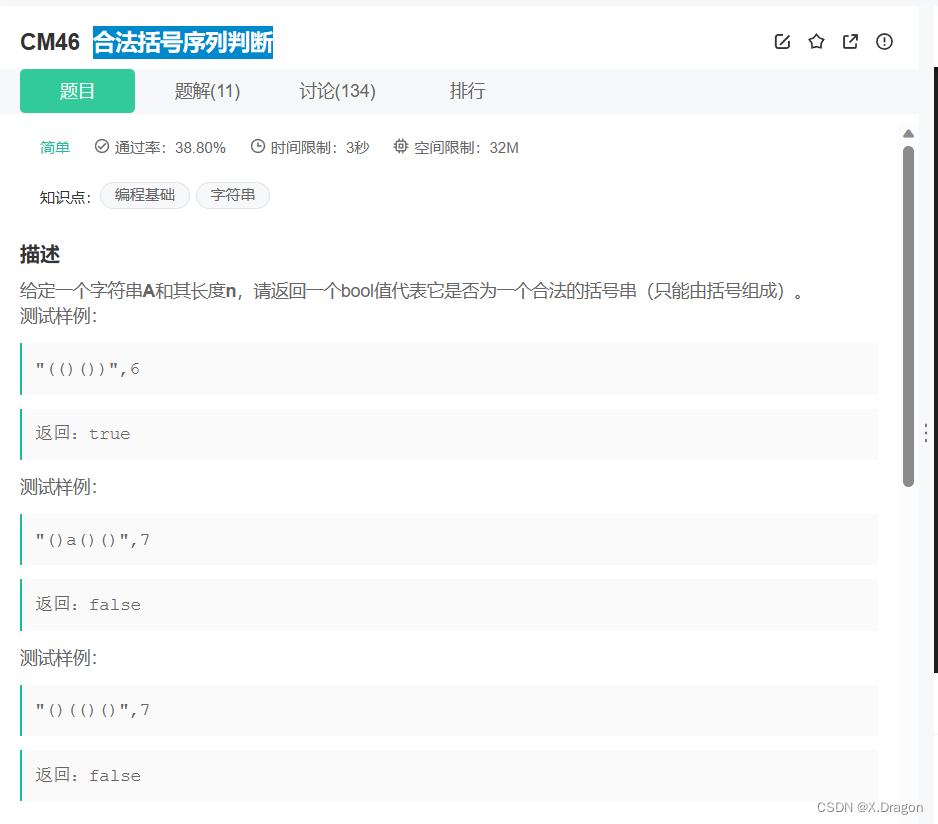
题目链接: 点击跳转
题解
题目解析】:
本题考查的是对栈的应用
【解题思路】:
用栈结构实现,栈中存放左括号,当遇到右括号之后,检查栈中是否有左括号,如果有则出栈,如果没有,则说明不匹配注意边界问题
代码
#include<stack>
class Parenthesis {
public:
bool chkParenthesis(string A, int n)
{
if(A.empty()&&(n%2)!=0)
return false;
stack<char> st;
for(int i=0;i<A.size();i++)
{
if(A[i]=='(')
{
st.push(A[i]);
}
else if(!st.empty()&&A[i]==')')
{
st.pop();
}
else
{
return false;
}
}
if(st.empty())
return true;
else
return false;
}
};
两种排序方法
题目:
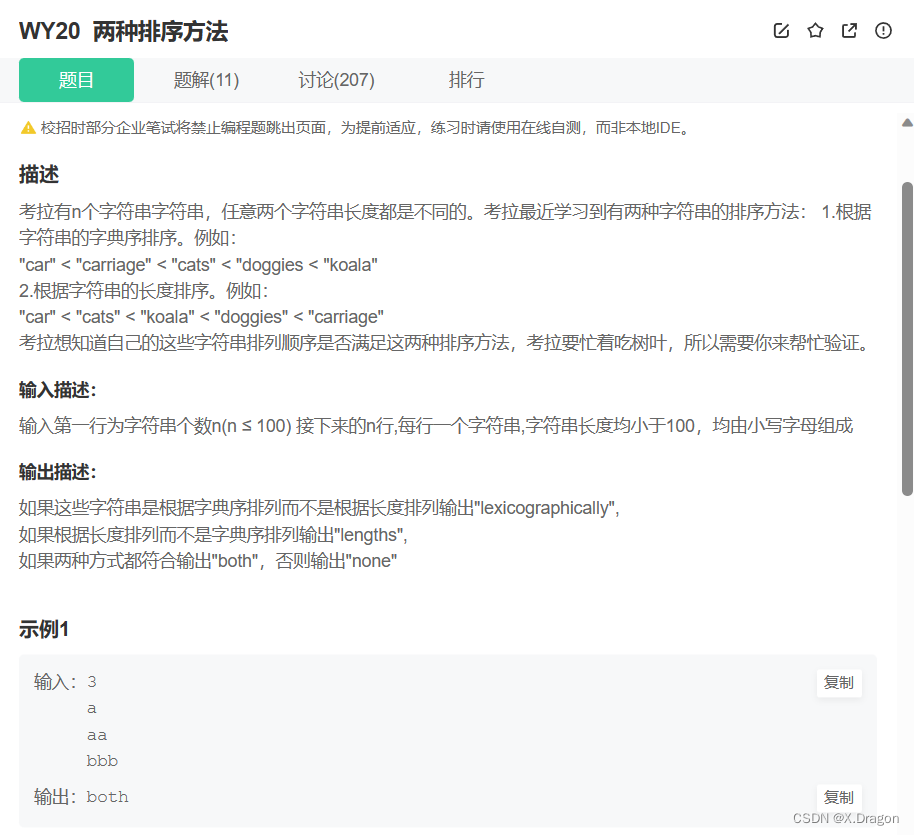
点击跳转: 两种排序方法
题解
思路很简单,将接受的字符串都放到vector容器中,利用string的operator>=运算符重载来按ascii比较字符串,利用string的size来比较字符串的长度
代码
#include<iostream>
#include<vector>
#include<string>
using namespace std;
int main()
{
int n;
cin>>n;
vector<string> v;
v.resize(n);
for(auto& str : v)
cin>>str;
bool lenSym = true, lexSym = true;
// 这里要注意从i=1开始遍历,前后比较,比较长度
for(size_t i = 1; i < v.size(); ++i)
{
if(v[i-1].size() >= v[i].size())
{
lenSym = false;
break;
}
}
//比较ASCII码
for(size_t i = 1; i < v.size(); ++i)
{
if(v[i-1] >= v[i])
{
lexSym = false;
break;
}
}
if (lenSym&& lexSym)
cout<<"both"<<endl;
else if (!lenSym && lexSym)
cout<<"lexicographically"<<endl;
else if (lenSym && !lexSym)
cout<<"lengths"<<endl;
else if (!lenSym&&!lexSym)
cout<<"none"<<endl;
return 0;
}