目录
- 数据结构:数组与特殊矩阵
- 数组
- 数组的特点
- 数组的用途
- 特殊矩阵
- 对角矩阵
- 上三角矩阵和下三角矩阵
- 稀疏矩阵
- 特殊矩阵的用途
- 结论
- 3.4 数组和特殊矩阵
- 3.4.1数组的存储结构
- 3.4.2普通矩阵的存储
- 3.4.3特殊矩阵的存储
- 1. 对称矩阵(方阵)
- 2. 三角矩阵(方阵)
- 3. 三对角矩阵(方阵)带状
- 4. 稀疏矩阵
数据结构:数组与特殊矩阵
数据结构是计算机科学中的基础概念,它涉及组织和存储数据的方式以及对数据的操作。在数据结构中,数组和特殊矩阵是两种常见的数据组织形式。本文将对数组和特殊矩阵进行介绍,并讨论它们在实际应用中的特点和用途。
数组
数组是一种线性数据结构,它由相同类型的元素按照一定顺序组成。数组的特点是在内存中连续存储元素,可以通过索引快速访问其中的元素。数组的索引通常从0开始,表示数组中元素的位置。例如,一个长度为n的数组A,其元素可以表示为A[0]、A[1]、A[2]、…、A[n-1]。
数组的特点
- 快速访问:由于数组中元素在内存中连续存储,可以通过索引直接访问数组中的元素,具有快速访问的特点。
- 固定大小:数组在创建时需要指定大小,且大小固定,无法在运行时动态改变大小。
- 存储效率高:由于元素在内存中连续存储,使得数组的存储效率较高。
数组的用途
数组在实际应用中有着广泛的用途,例如:
- 数据存储:用于存储一系列数据元素,如整数、字符、浮点数等。
- 数据统计:用于统计一组数据中的最大值、最小值、平均值等。
- 排序算法:在各种排序算法中,数组是常用的数据结构。
数组的使用非常灵活,它在算法和数据处理领域有着重要的地位。
特殊矩阵
特殊矩阵是一种二维数据结构,它具有某种特殊的规律或特点,使得在特定情况下能够对其进行更高效的存储和操作。特殊矩阵通常有以下几种类型:
对角矩阵
对角矩阵是一种除了主对角线以外的所有元素都为零的矩阵。例如,一个n阶对角矩阵D可以表示为:
d[i][j] = 0, i ≠ j
d[i][j] ≠ 0, i = j
对角矩阵在存储和运算时,可以只保存主对角线上的元素,大大节省了存储空间和运算时间。
上三角矩阵和下三角矩阵
上三角矩阵和下三角矩阵是一种在主对角线上方或下方的所有元素都为零的矩阵。上三角矩阵的下方元素都为零,下三角矩阵的上方元素都为零。这些矩阵在存储和运算时,也可以只保存非零元素,节省存储空间和运算时间。
稀疏矩阵
稀疏矩阵是一种大部分元素都为零的矩阵。在实际应用中,很多矩阵都是稀疏矩阵,例如图像处理中的像素矩阵。对于稀疏矩阵,存储所有元素将会浪费大量的存储空间。因此,可以采用压缩存储方法,只存储非零元素及其位置,从而节省存储空间。
特殊矩阵的用途
特殊矩阵在很多领域都有着广泛的应用,尤其在数值计算和科学工程中。它们可以优化矩阵的存储和运算效率,提高算法的执行速度。
结论
数组和特殊矩阵是两种常见的数据结构,在计算机科学和工程中都有着广泛的应用。数组是一种简单而高效的数据组织形式,用于存储一系列相同类型的元素。特殊矩阵是一种具有特殊规律的二维数据结构,能够优化矩阵的存储和运算效率。
在实际应用中,我们可以根据具体问题的特点选择合适的数据结构,以提高算法的效率和性能。同时,对于特殊矩阵,我们可以采用压缩存储方法来节省存储空间,使得数据处理更加高效和便捷。通过合理选择和使用数据结构,我们可以优化算法的执行效率,提高计算机程序的性能。
3.4 数组和特殊矩阵
矩阵定义: 一个由m*n个元素排成的m行(横向)n列(纵向)的表。
矩阵的常规存储:将矩阵描述为一个二维数组。
3.4.1数组的存储结构
- 一维数组
Elemtype a[10];
各数组元素大小相同,物理上连续存放;
起始地址:LOC
数组下标:默认从0开始!
数组元素 a[i] 的存放地址 = LOC + i × sizeof(ElemType)

- 二维数组
Elemtype b[2][4]; //2行4列的二维数组
行优先/列优先存储优点:实现随机存储

起始地址:LOC
M行N列的二维数组 b[M][N] 中,b[i][j]的存储地址:
行优先存储: LOC + (i×N + j) × sizeof(ElemType)
列优先存储:LOC + (j×M + i) × sizeof(ElemType)
3.4.2普通矩阵的存储
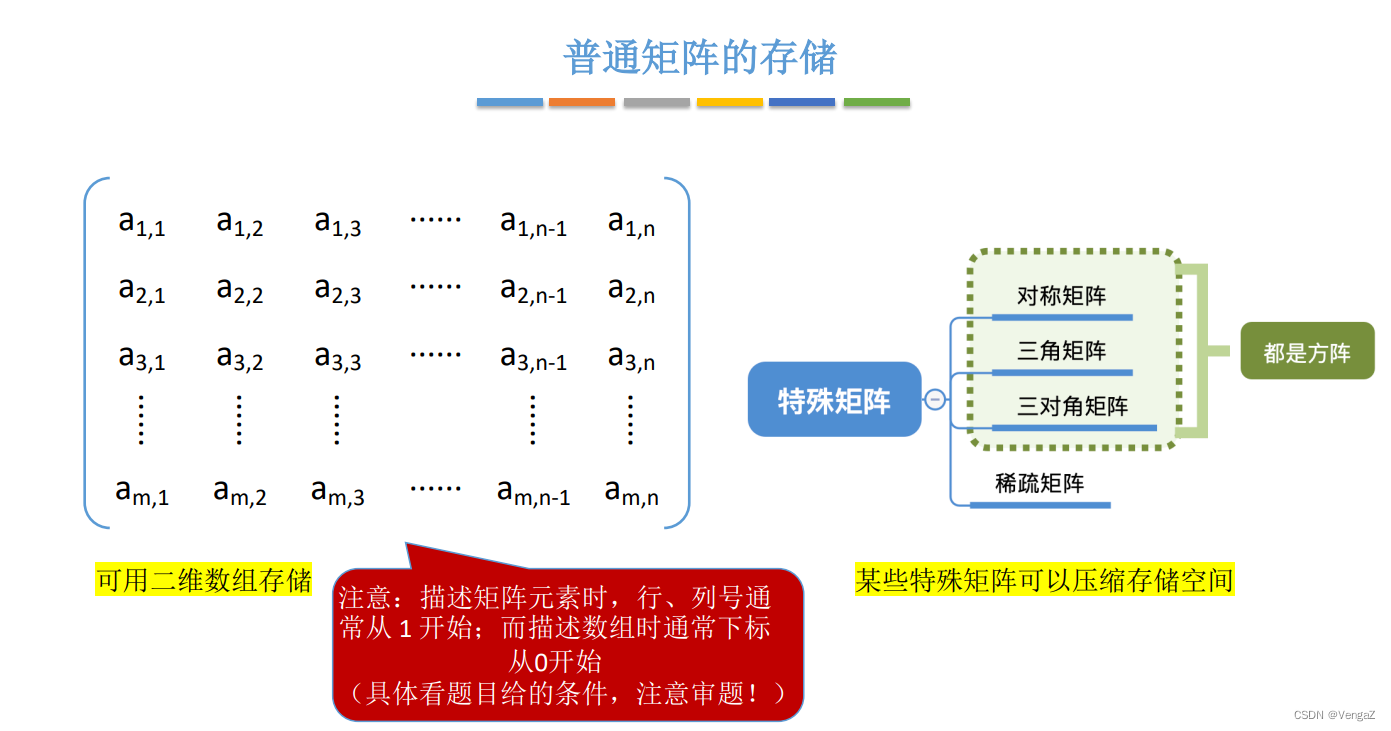
二维数组存储:
- 描述矩阵元素时,行、列号通常从1开始;
- 描述数组时,通常下标从 0 开始;
3.4.3特殊矩阵的存储
特殊矩阵——压缩存储空间(只存有用的数据)
矩阵的压缩存储:为多个相同的非零元素只分配一个存储空间;对零元素不分配空间。
1. 对称矩阵(方阵)
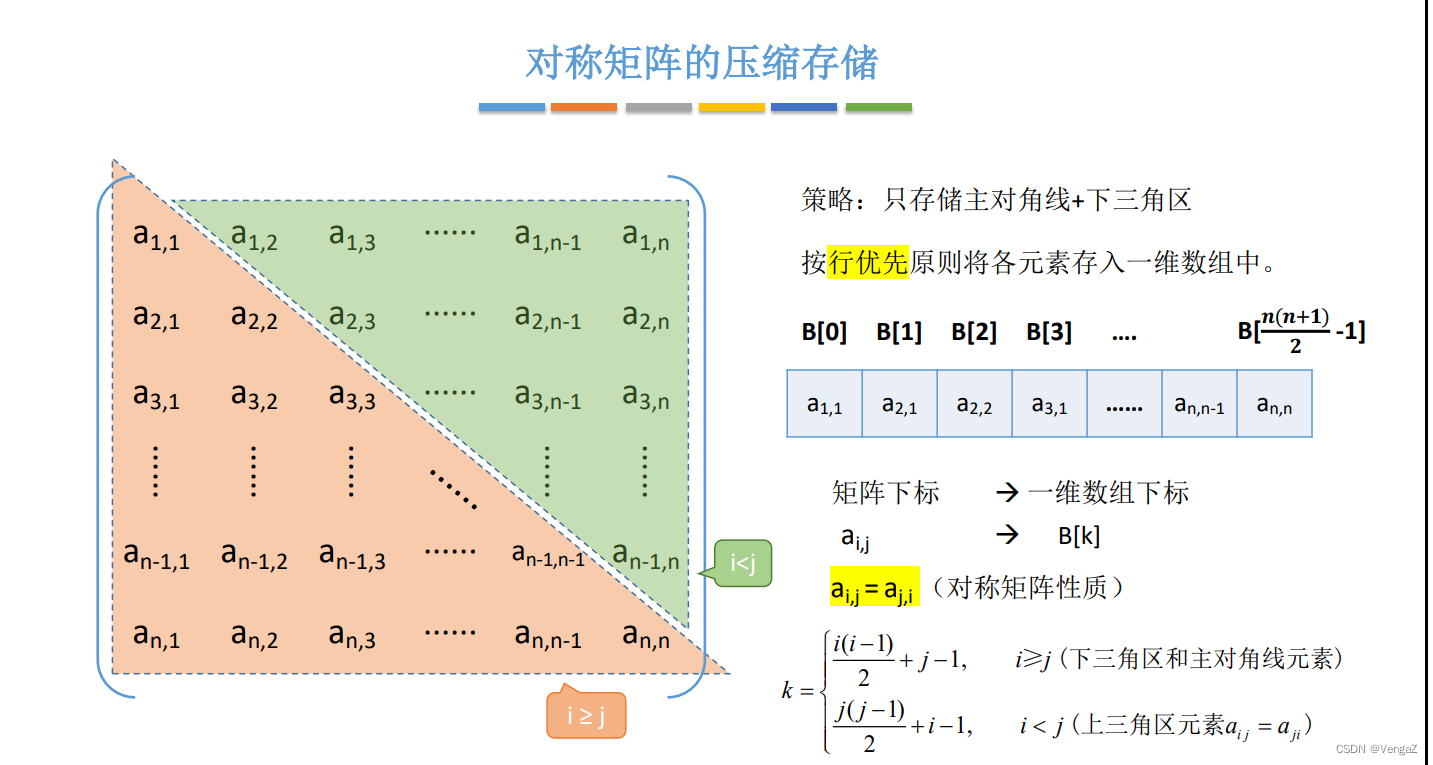
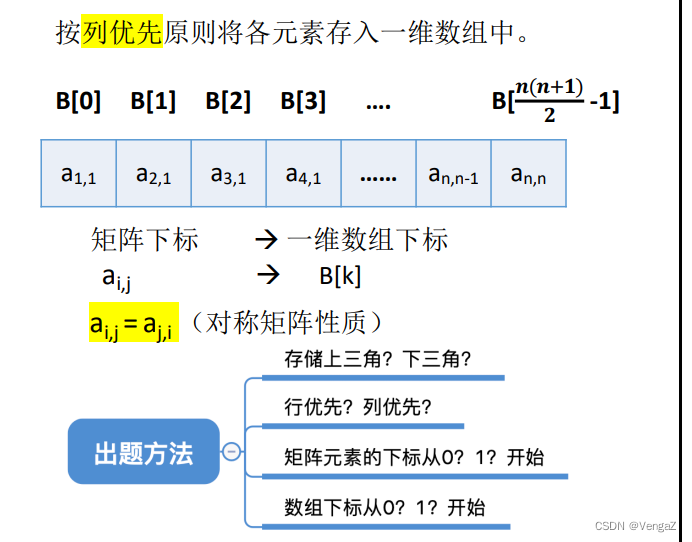
列优先:
-
n >1
n+ (n-1)+ ······+(i-j)+1 -
n = 1
i-j+1
2. 三角矩阵(方阵)
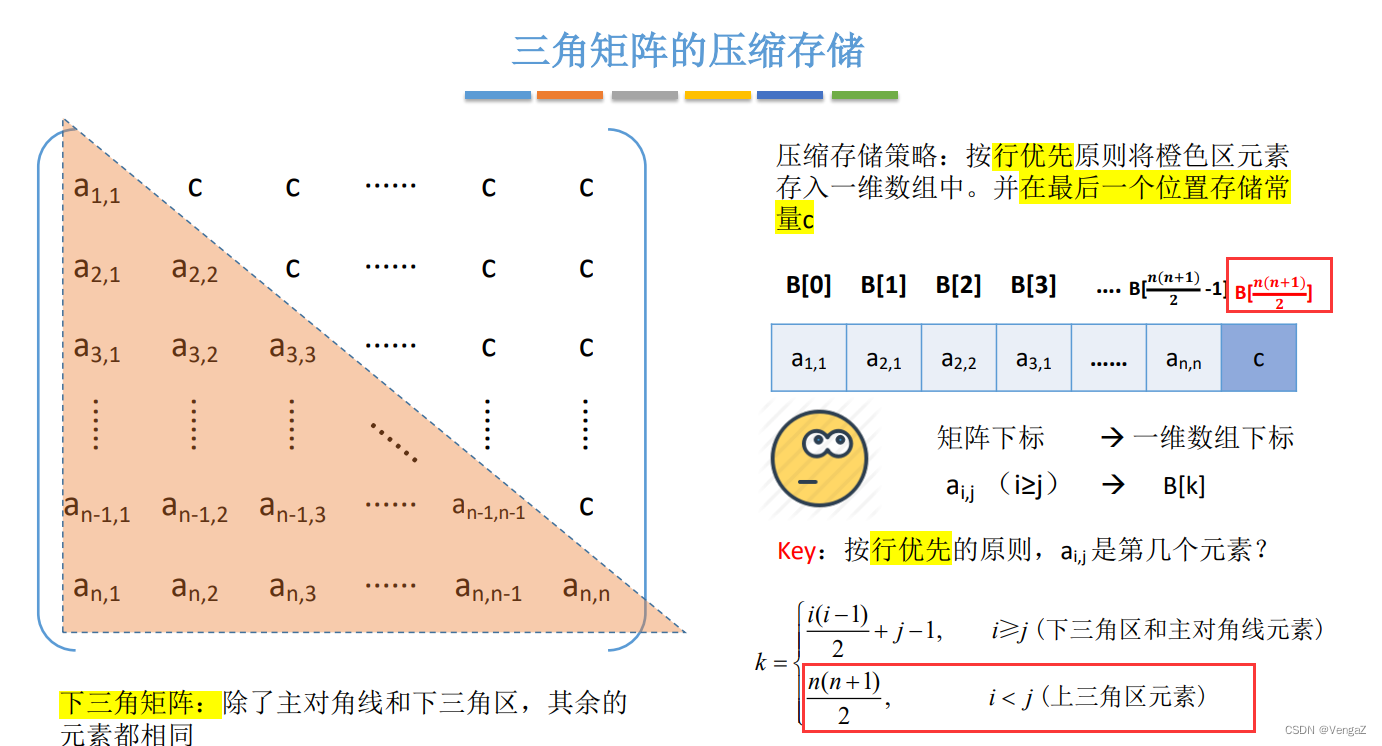
n + (n-1) +······(n-i+1) +(j-i)
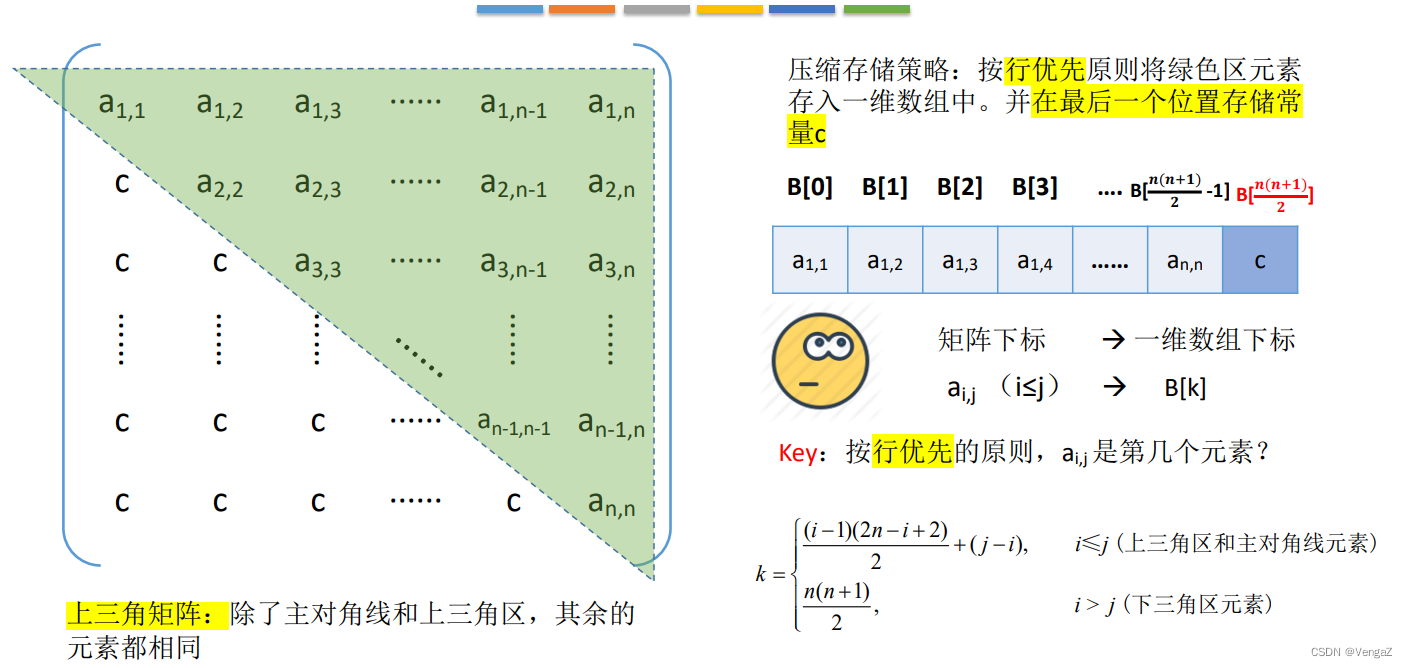
3. 三对角矩阵(方阵)带状
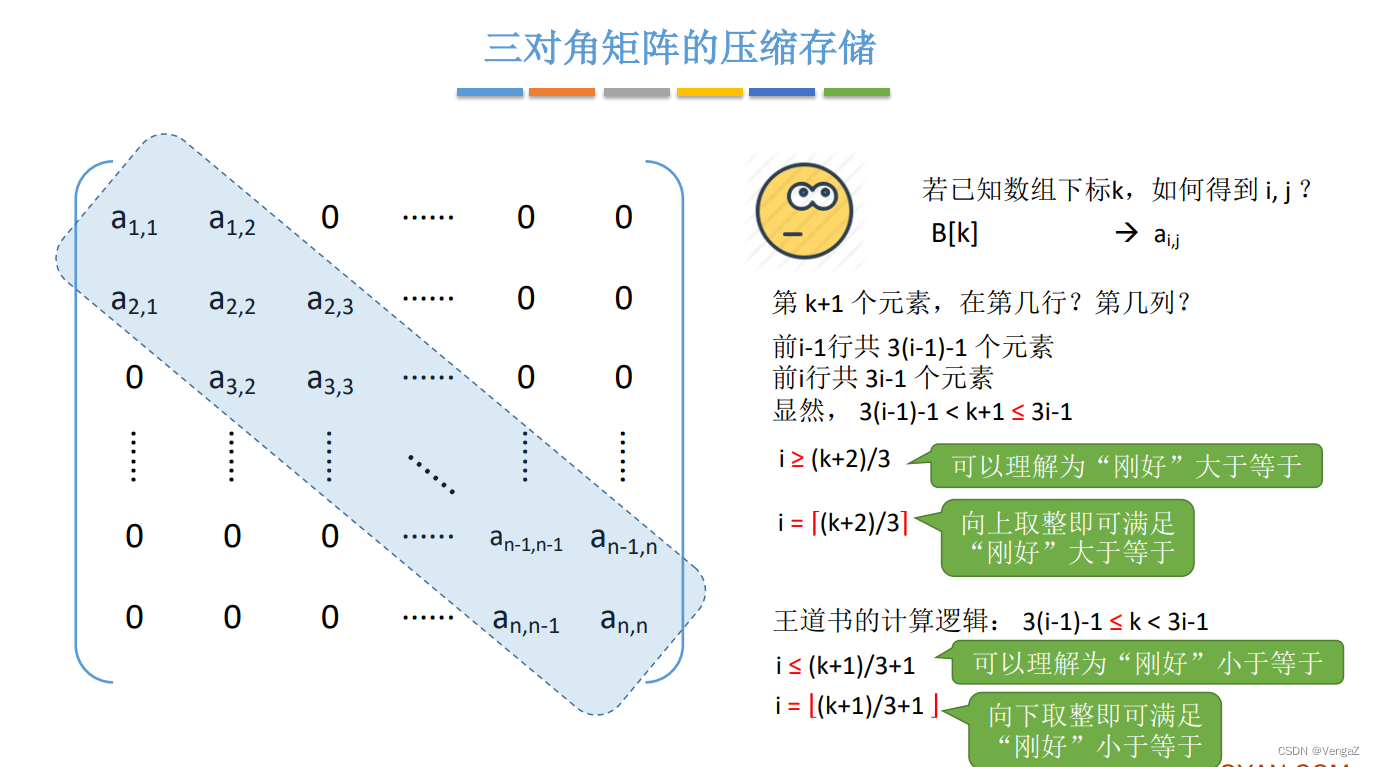

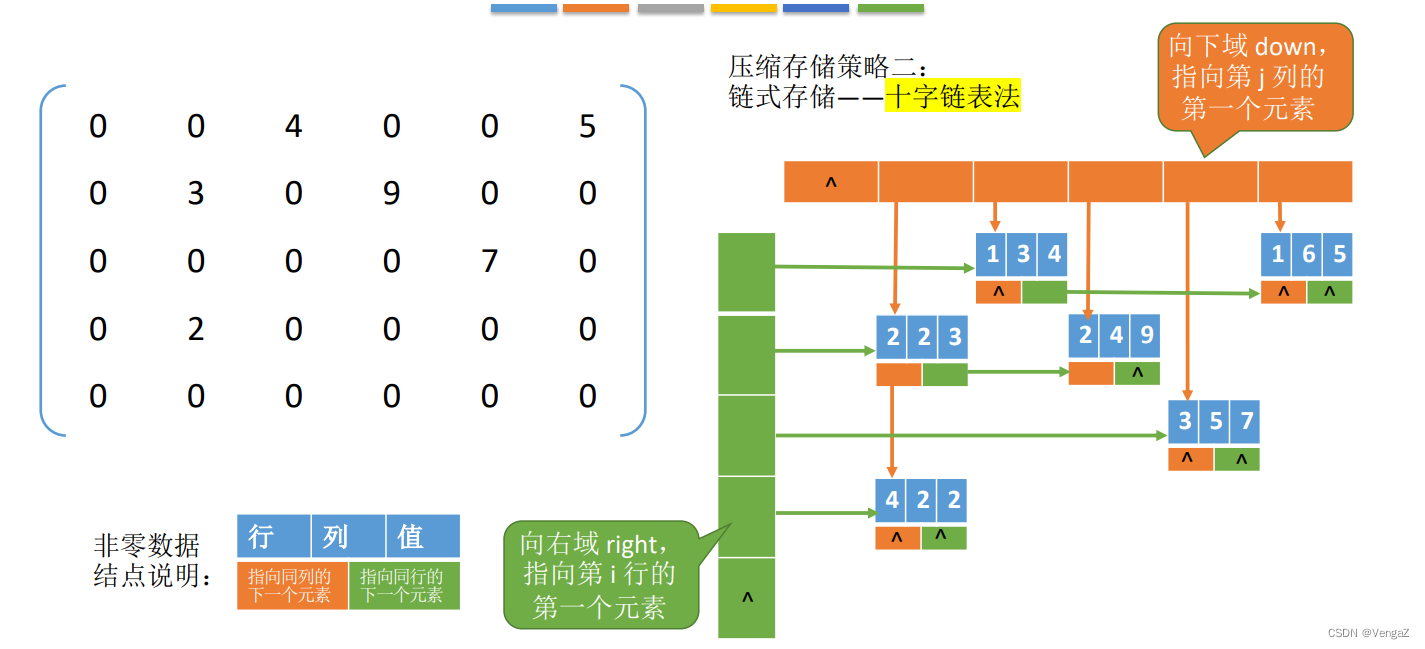
4. 稀疏矩阵
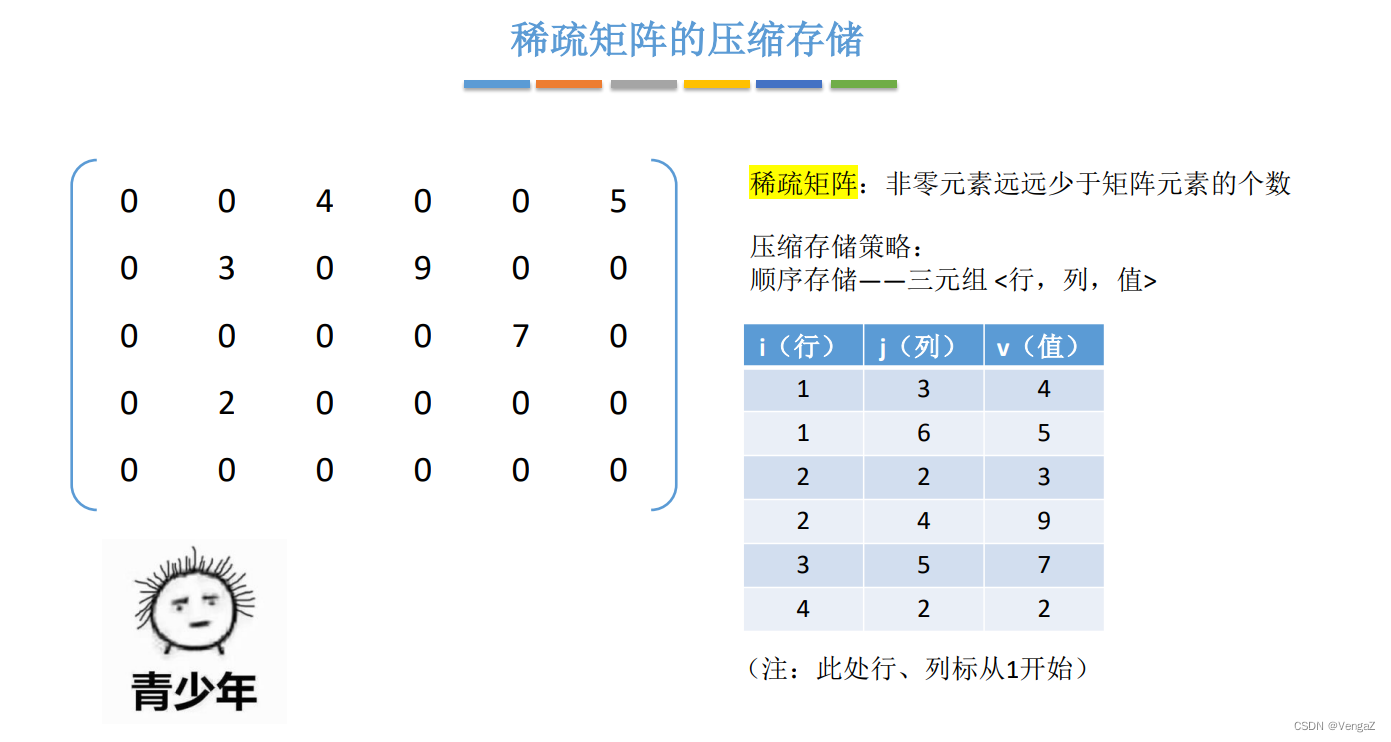
设在mn的矩阵中有t个非零元素,令c=t/(mn),当c<=0.05时称为稀疏矩阵。
压缩存储原则:存各非零元的值、行列位置和矩阵的行列数。