文章目录
- 二叉树性质
- 二叉树分类
- 遍历二叉树
- 如何判断是否为完全二叉树
二叉树是树形结构的一个重要类型。许多实际问题抽象出来的数据结构往往是二叉树形式,即使是一般的树也能简单地转换为二叉树,而且二叉树的存储结构及其算法都较为简单,因此二叉树显得特别重要。二叉树特点是每个节点最多只能有两棵子树,且有左右之分。
二叉树是n个有限元素的集合,该集合或者为空、或者由一个称为根(root)的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成,是有序树。当集合为空时,称该二叉树为空二叉树。在二叉树中,一个元素也称作一个节点
二叉树性质
二叉树是一种特殊的树结构,具有一些重要的性质。这些性质对于理解和操作二叉树非常有帮助。以下是二叉树的一些主要性质:
-
每个节点最多有两个子节点:每个节点最多包含两个子节点,通常称为左子节点和右子节点。这个特性是二叉树最基本的特征。
-
左子树和右子树:二叉树的每个节点都可以看作是根节点,它们分别有自己的左子树和右子树。这使得二叉树具有递归结构。
-
树的深度(Depth):树的深度是从根节点到最远叶节点的最长路径的节点数。树的深度可以用来评估树的高度。
- 第i层最多有2^(i-1)个节点(i>=1)
- 深度为k的二叉树最多有2^k - 1个节点(k>=1)。
- 含有n个节点的二叉树深度至少有log2(n+1)
- 树的高度(Height):树的高度是从根节点到最远叶节点的最长路径的边数。树的高度可以用来评估树的复杂性和性能。
- 高度为h的二叉树,最少有h个节点,最多有2^h - 1个节点。
- 对于任意的二叉树,其最大宽度都是2^h - 1,h为其高度。
-
叶节点(Leaf):没有子节点的节点称为叶节点,也称为终端节点。叶节点位于树的末端。
-
内部节点(Internal Node):除了根节点和叶节点,其他节点都是内部节点,即有至少一个子节点的节点。
-
兄弟节点(Sibling):具有相同父节点的节点称为兄弟节点。
-
祖先节点(Ancestor):位于某节点到根节点路径上的所有节点都是该节点的祖先节点。
-
子孙节点(Descendant):某节点的子树中的所有节点都是该节点的子孙节点。
-
二叉搜索树性质:对于二叉搜索树(BST),它是一种特殊的二叉树,有以下性质:
- 左子树中的所有节点的值小于等于父节点的值。
- 右子树中的所有节点的值大于等于父节点的值。
- 左右子树也分别是二叉搜索树。
- 完全二叉树性质:完全二叉树是一种特殊的二叉树,具有以下性质:
- 除了最后一层外,其他层的节点都是满的,且最后一层的节点从左向右排列。
- 满二叉树性质:满二叉树是一种特殊的二叉树,具有以下性质:
- 除了叶节点外,每个节点都有两个子节点。
二叉树分类
-
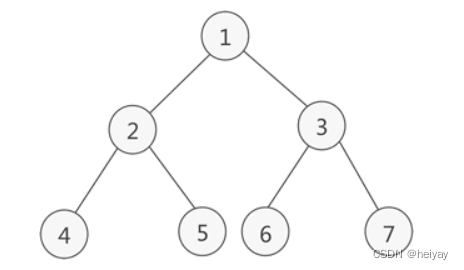
满二叉树:每一层上的节点数都是最大节点数。
-
完全二叉树:除了最后一层,其他层都是满的,最后一层的节点都靠左排列。
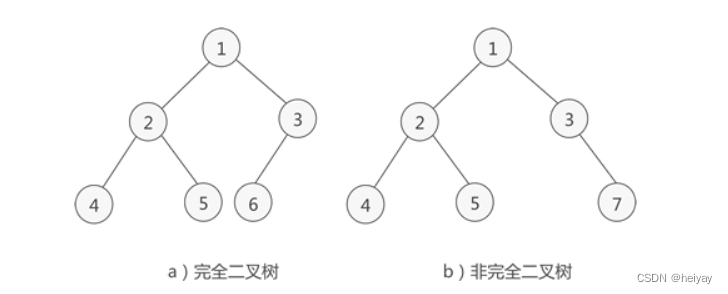
-
二叉搜索树(BST):左子树的值小于根节点,右子树的值大于根节点。
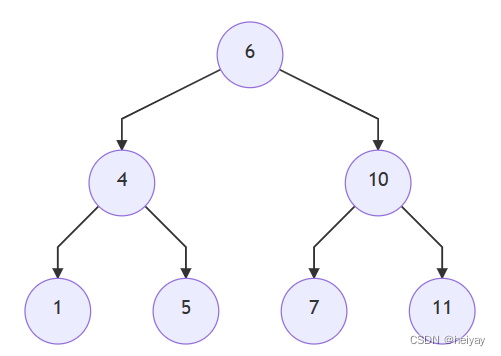
-
平衡二叉树:左右子树的高度差不超过1,通常用来提高搜索性能。
-
红黑树:每个节点标记红黑色,通过颜色保持自平衡,是一种平衡二叉树。
-
B树和B+树:扩展的多叉树,可用于数据库索引。
遍历二叉树
- 前序遍历:根节点 —> 左子树 —> 右子树
- 中序遍历:左子树 —> 根节点 —> 右子树
- 后序遍历:左子树 —> 右子树 —> 根节点
- 层序遍历:按层次一层一层遍历节点
js
// 二叉树节点类
class Node {
constructor(val) {
this.val = val;
this.left = null;
this.right = null;
}
}
// 前序遍历
function preorder(root) {
if (!root) return [];
let result = [root.val];
result = result.concat(preorder(root.left));
result = result.concat(preorder(root.right));
return result;
}
// 中序遍历
function inorder(root) {
if (!root) return [];
let result = [];
result = result.concat(inorder(root.left));
result.push(root.val);
result = result.concat(inorder(root.right));
return result;
}
// 后序遍历
function postorder(root) {
if (!root) return [];
let result = [];
result = result.concat(postorder(root.left));
result = result.concat(postorder(root.right));
result.push(root.val);
return result;
}
// 层序遍历
function levelorder(root) {
let result = [];
let queue = [root];
while (queue.length) {
let curr = queue.shift();
result.push(curr.val);
if (curr.left) queue.push(curr.left);
if (curr.right) queue.push(curr.right);
}
return result;
}
let root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
// 分别测试不同遍历函数
console.log(preorder(root)); // [1, 2, 4, 5, 3]
console.log(inorder(root)); // [4, 2, 5, 1, 3]
console.log(postorder(root)); // [4, 5, 2, 3, 1]
console.log(levelorder(root)); // [1, 2, 3, 4, 5]
如何判断是否为完全二叉树
判断一棵二叉树是否是完全二叉树可以通过广度优先搜索(BFS)的方式进行。在BFS的过程中,我们需要对树中的每个节点进行遍历,并按层级顺序将节点加入队列。对于完全二叉树来说,遇到第一个空节点后,其后的所有节点都应该是空节点,否则就不是完全二叉树。
下面给出使用BFS判断是否是完全二叉树的JavaScript代码:
class TreeNode {
constructor(data) {
this.data = data;
this.left = null;
this.right = null;
}
}
function isCompleteBinaryTree(root) {
if (!root) return true;
const queue = [root];
let flag = false; // 用来标记是否遇到第一个空节点
while (queue.length > 0) {
const node = queue.shift();
// 如果遇到第一个空节点
if (!node) {
flag = true;
} else {
// 如果已经遇到空节点,但当前节点不是空节点,则不是完全二叉树
if (flag) return false;
queue.push(node.left);
queue.push(node.right);
}
}
return true;
}
// 示例用法:
const binaryTree = new TreeNode(1);
binaryTree.left = new TreeNode(2);
binaryTree.right = new TreeNode(3);
binaryTree.left.left = new TreeNode(4);
binaryTree.left.right = new TreeNode(5);
binaryTree.right.left = new TreeNode(6);
binaryTree.right.right = new TreeNode(7);
console.log(isCompleteBinaryTree(binaryTree)); // 打印: true
创建了一个二叉树,并用isCompleteBinaryTree函数判断这棵树是否是完全二叉树。根据给定的二叉树,结果应该为true。