文章目录
- 基本概念
- 基本操作
- 实现分析
- 插入数据
- 查找数据
- 删除数据
- 遍历数据
- 源码
基本概念
二叉搜索树也叫搜索二叉树、二叉排序树、排序二叉树。是一种对查找和排序都有用的特殊二叉树。
二叉搜索树(Binary Search Tree,简称BST)
如何构建一颗二叉搜索树
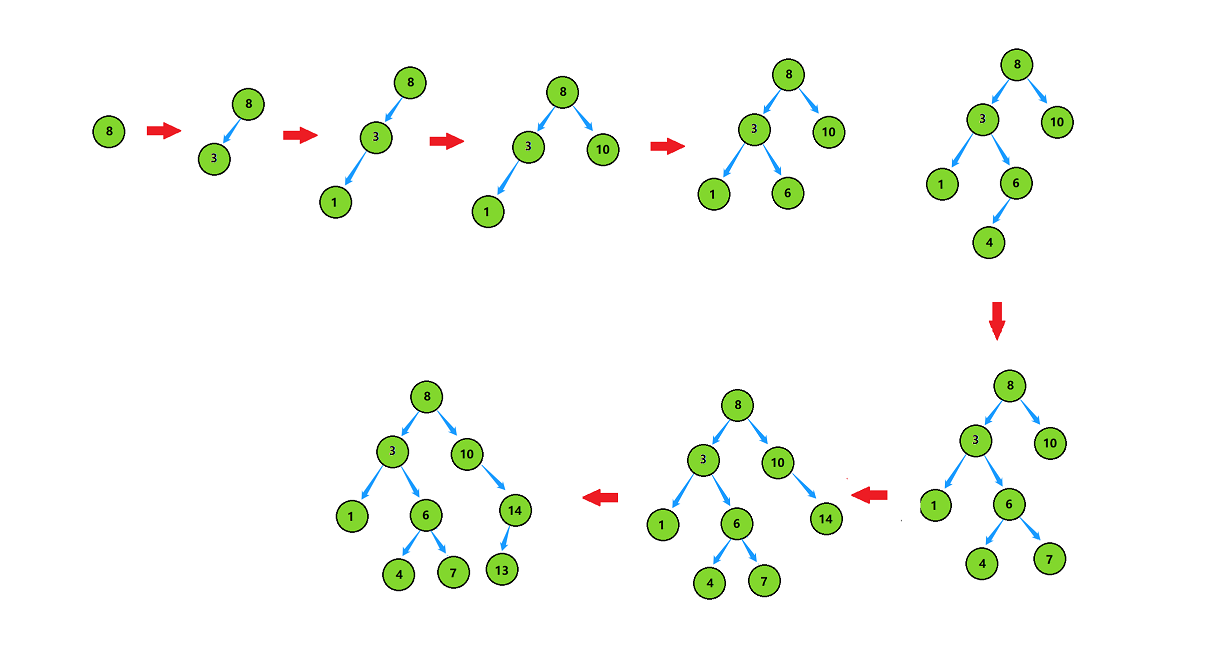
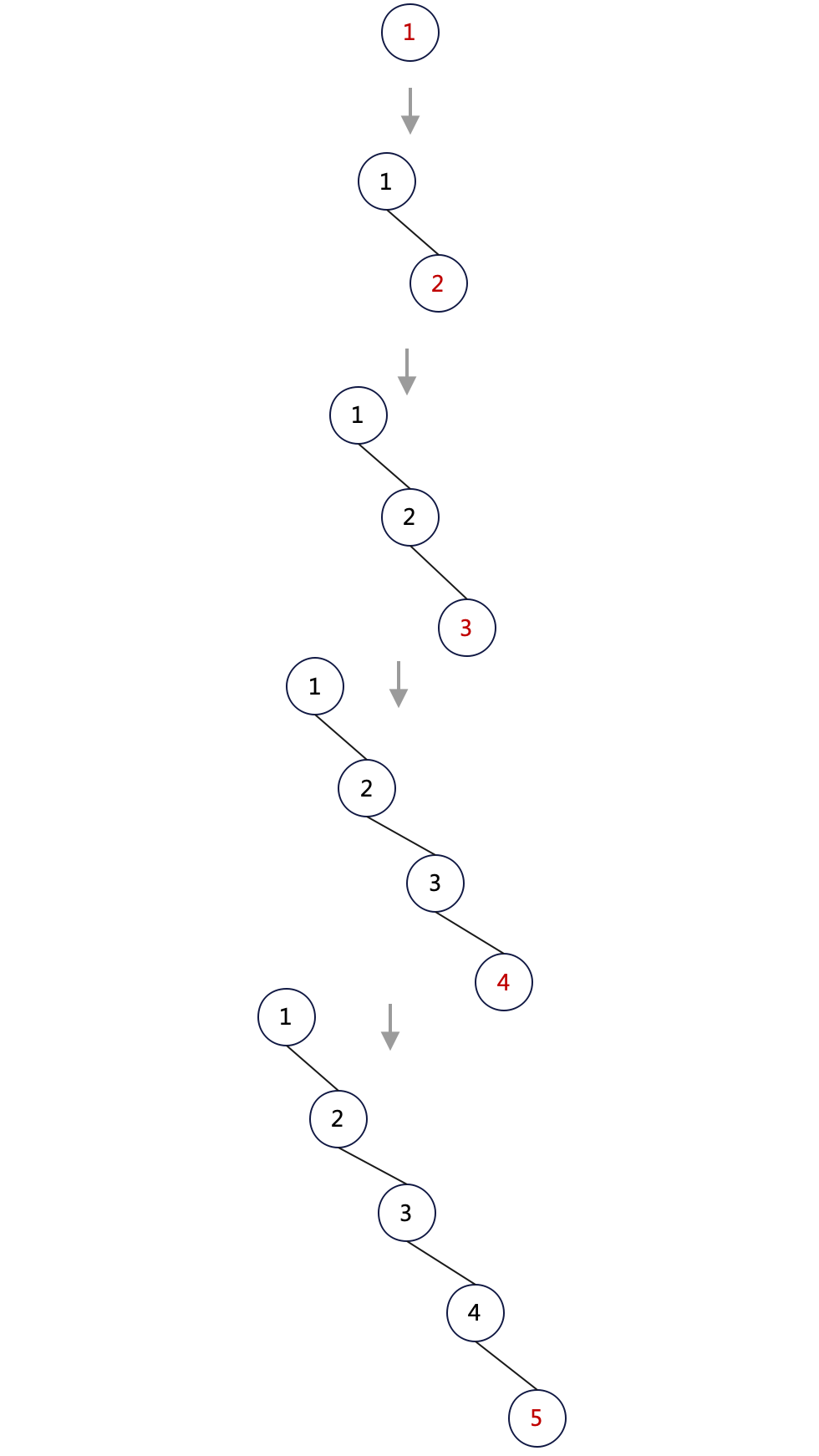
假设我们有如下数据,我们按从左往右的顺序构建一颗二叉搜索树

1.首先,将8作为根节点
2.插入3,由于3小于8,作为8的左子树
3.插入1,由于1小于8,进入左子树3,1又小于3,则1为3的左子树
4.插入10,由于10大于8,则作为8的右子树
5.插入6,由于6小于8,进入左子树3,6又大于3,则6为3的右子树
6.插入4,由于4小于8,进入左子树3,4又大于3,进入右子树6,4还小于6,则4为6的左子树
7.插入7,由于7小于8,进入左子树3,7又大于3,进入右子树6,7还大于于6,则7为6的右子树
8.插入14,由于14大于8,进入右子树10,14又大于10,则14为10的右子树
9.插入13,由于13大于8,进入右子树10,又13大于10,进入右子树14,13小于14,则13为14的左子树
构建一颗二叉搜索树
①只要左子树为空,就把小于父节点的数插入作为左子树
②只要右子树为空,就把大于父节点的数插入作为右子树
③如果不为空,就一直往下去搜索,直到找到合适的插入位置
基本操作
二叉搜索树,又名二叉排序数,是因为这颗二叉树在使用中序遍历来遍历这颗二叉树的时候数据呈现升序,所以我们使用中序遍历来遍历二叉树
插入数据
删除数据
查找数据
查找元素
实现分析
插入数据
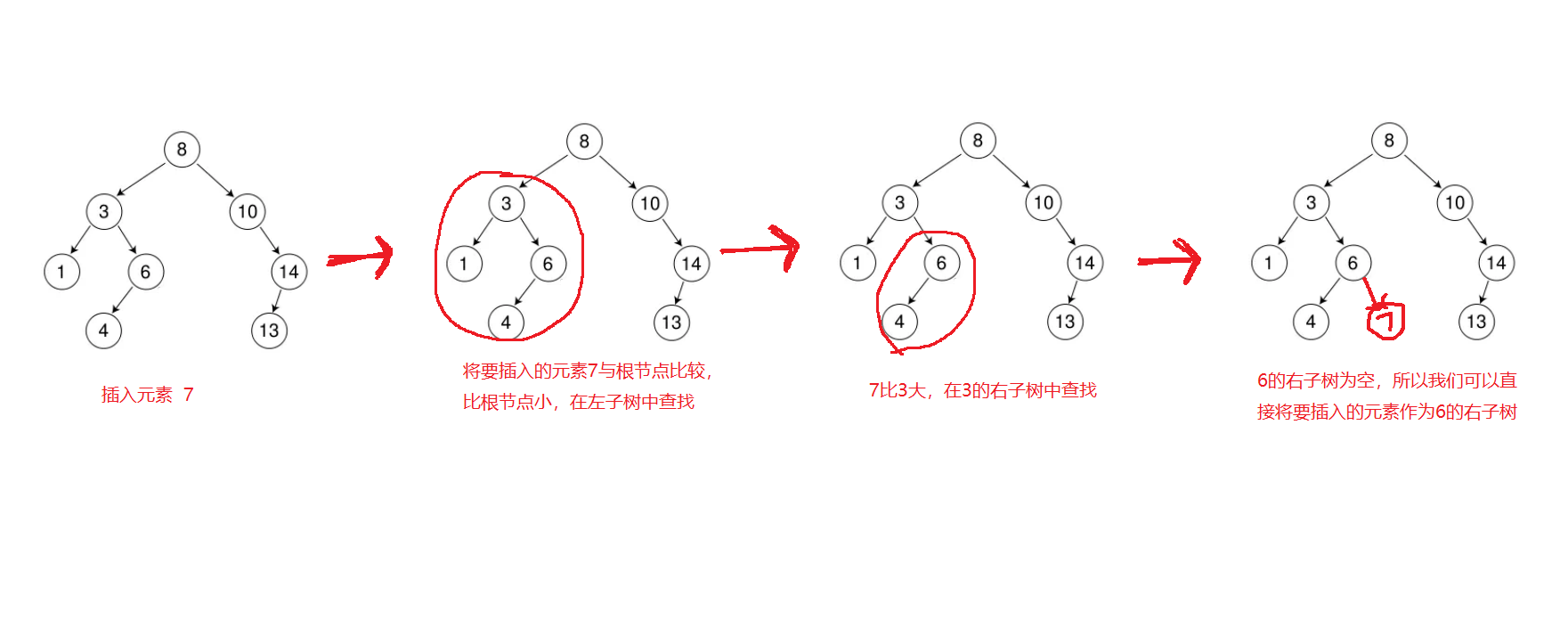
构造一颗二叉搜索树的过程就是插入过程,找寻要插入元素的位置的规则,将要插入的数据与根节点比较,如果比根节点大,则在右子树中寻找,再将要插入的元素跟右子树的根节点比较,如果大,则继续在右子树中找,反之。以此类推,一直找到空节点,如果要插入的元素比根节点小,就将要插入的元素与根节点的左子树比较,同上。
bool Insert(const K& key)
{
//判断特殊情况,如果根节点为空,则将要插入的元素作为根节点
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
//相同值,插入失败
return false;
}
}
cur = new Node(key);
if (parent->_key > key)parent->_left = cur;
else parent->_right = cur;
return true;
}
查找数据
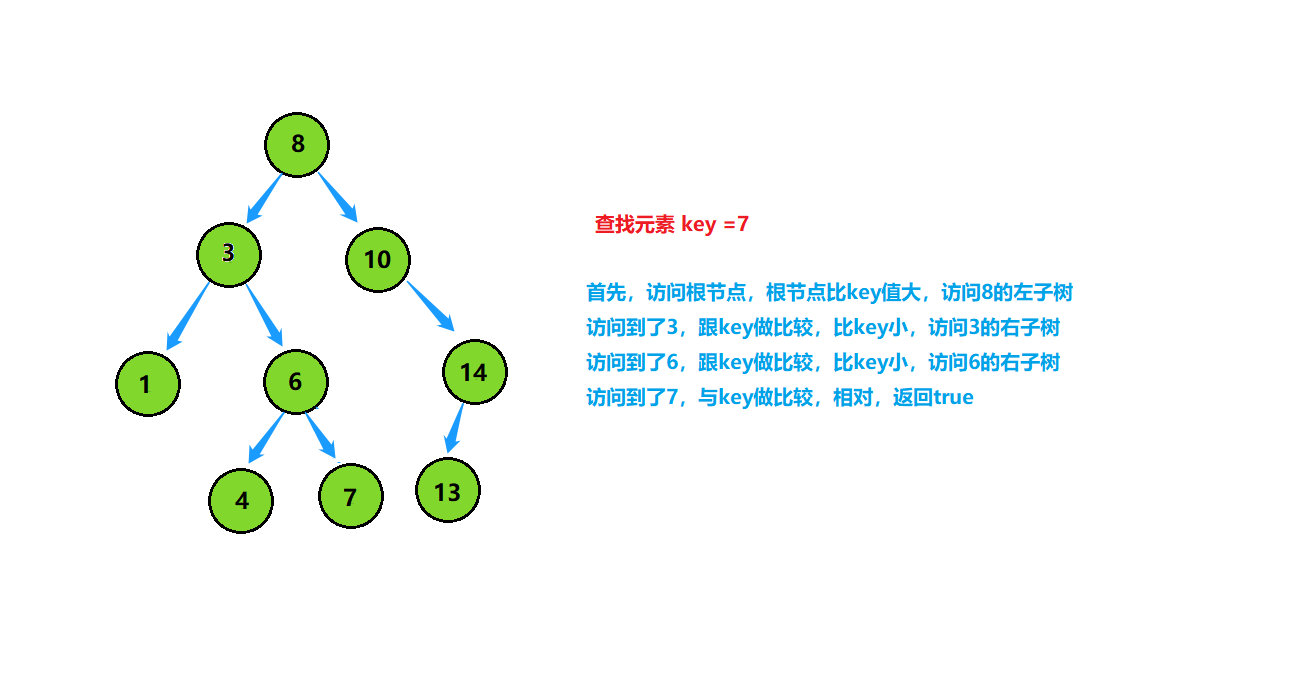
它既然也叫二叉搜索树,查找数据非常的便利。它的操作并不是把中序遍历的结果存入数组,然后在有序数组里查找,而是直接在树上查找。其操作与二分查找非常相似,我们来查找7试一试?(这里要说明以下:在正常的数据结构中,由于数据量很大,所以我们也不知道我们想要的元素在不在里面;同时也不知道每个元素具体是多少,只知道他们的大小关系。我们是在此基础上进行查找)
bool Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else {
return true;
}
}
return false;
}
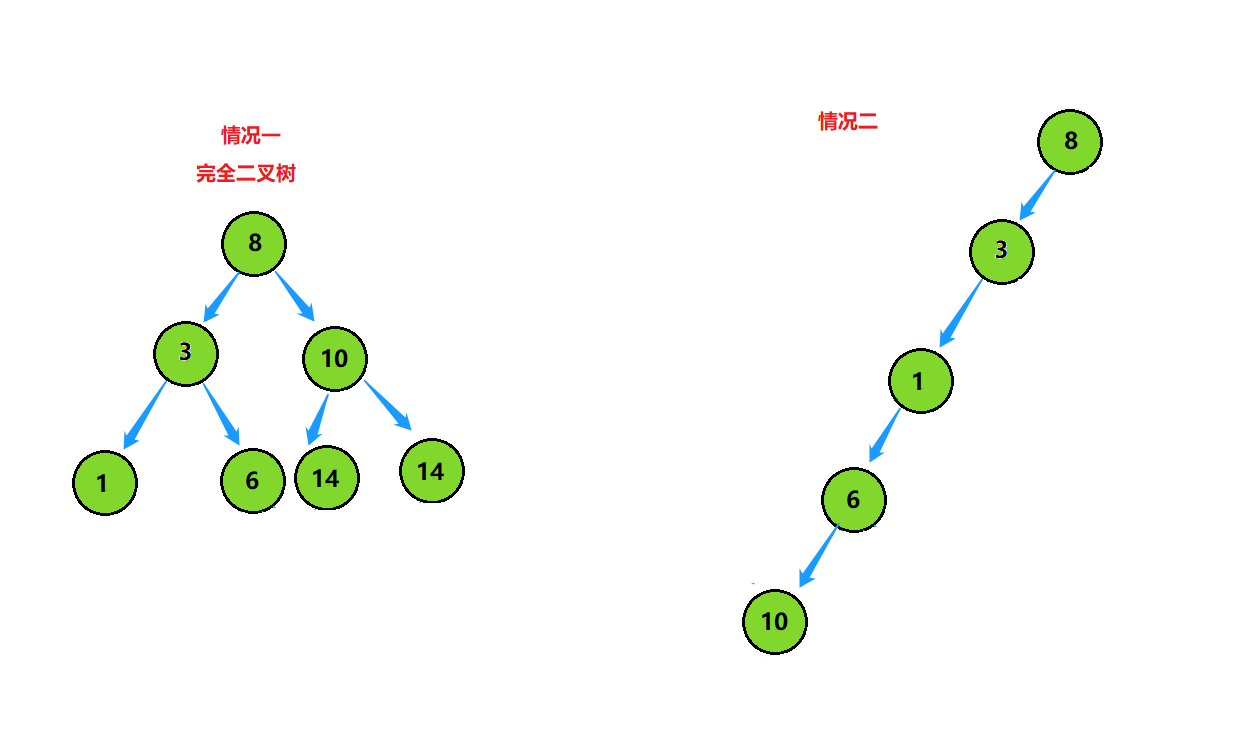
搜索二叉树的查找数据也不是很快,查找一个元素的最快时间复杂度是O(logn)(图左),最坏时间复杂度是O(n)(图右)
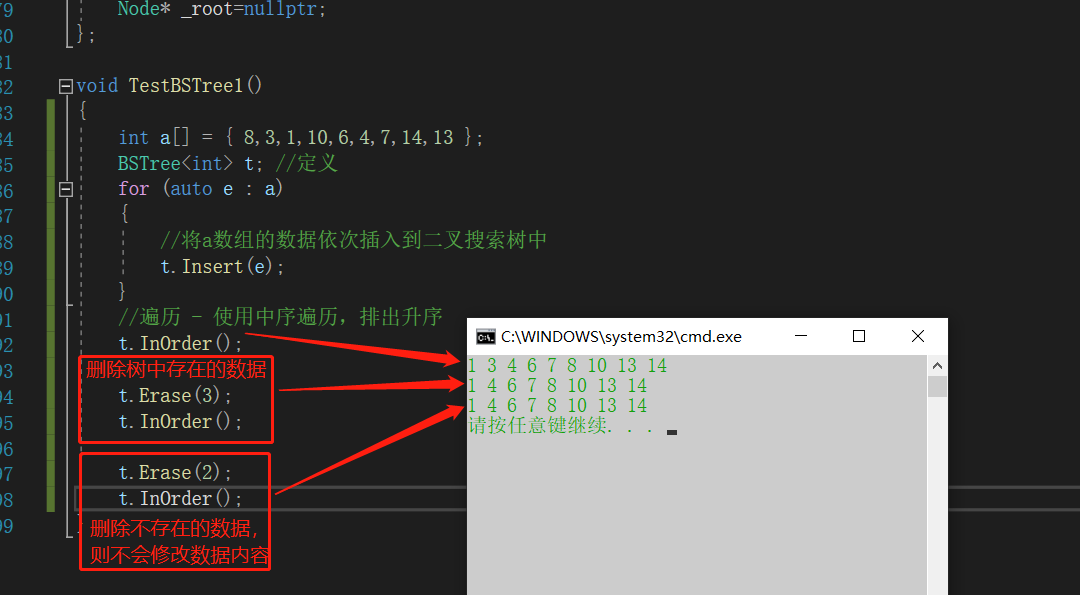
删除数据
二叉树的删除要复杂一点,需要分类讨论分三种情况
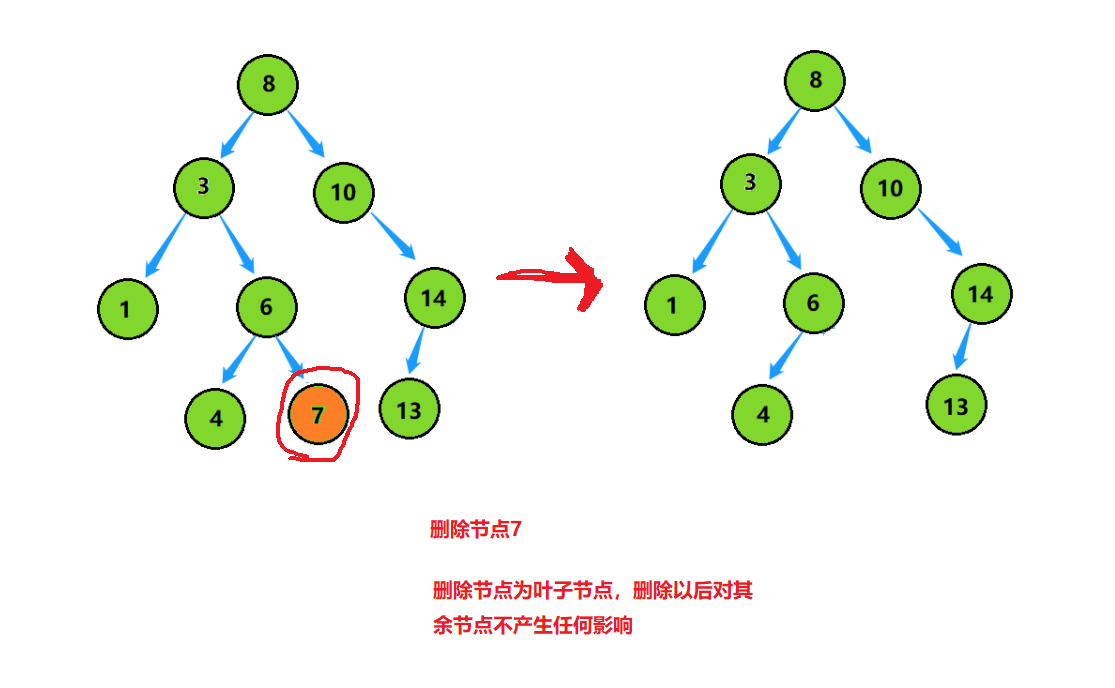
情况一 删除叶子节点
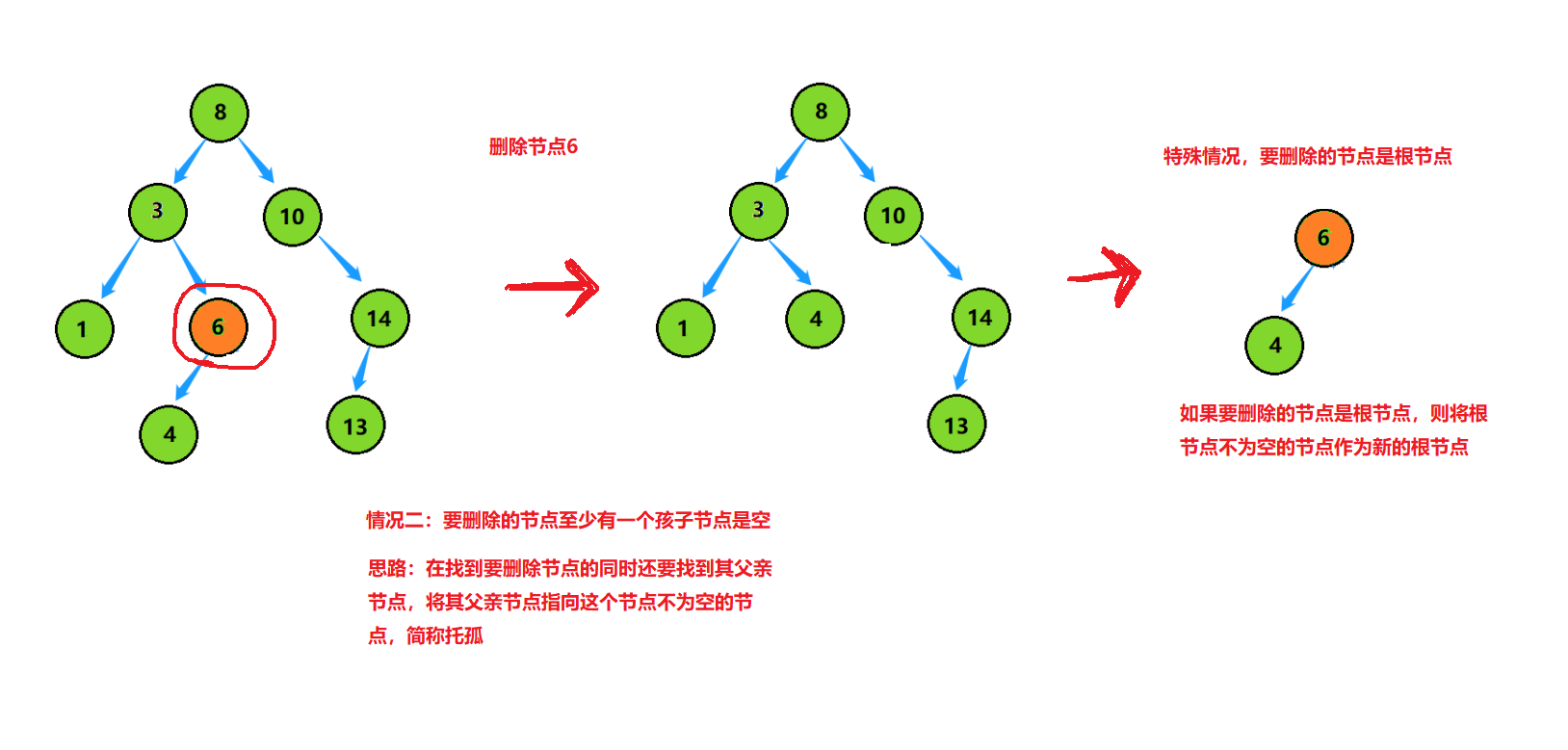
情况二: 要删除的节点至少一个孩子为空
这两种情况可以写代码时可归为一类,就是将删除节点的子节点托孤给父亲节点
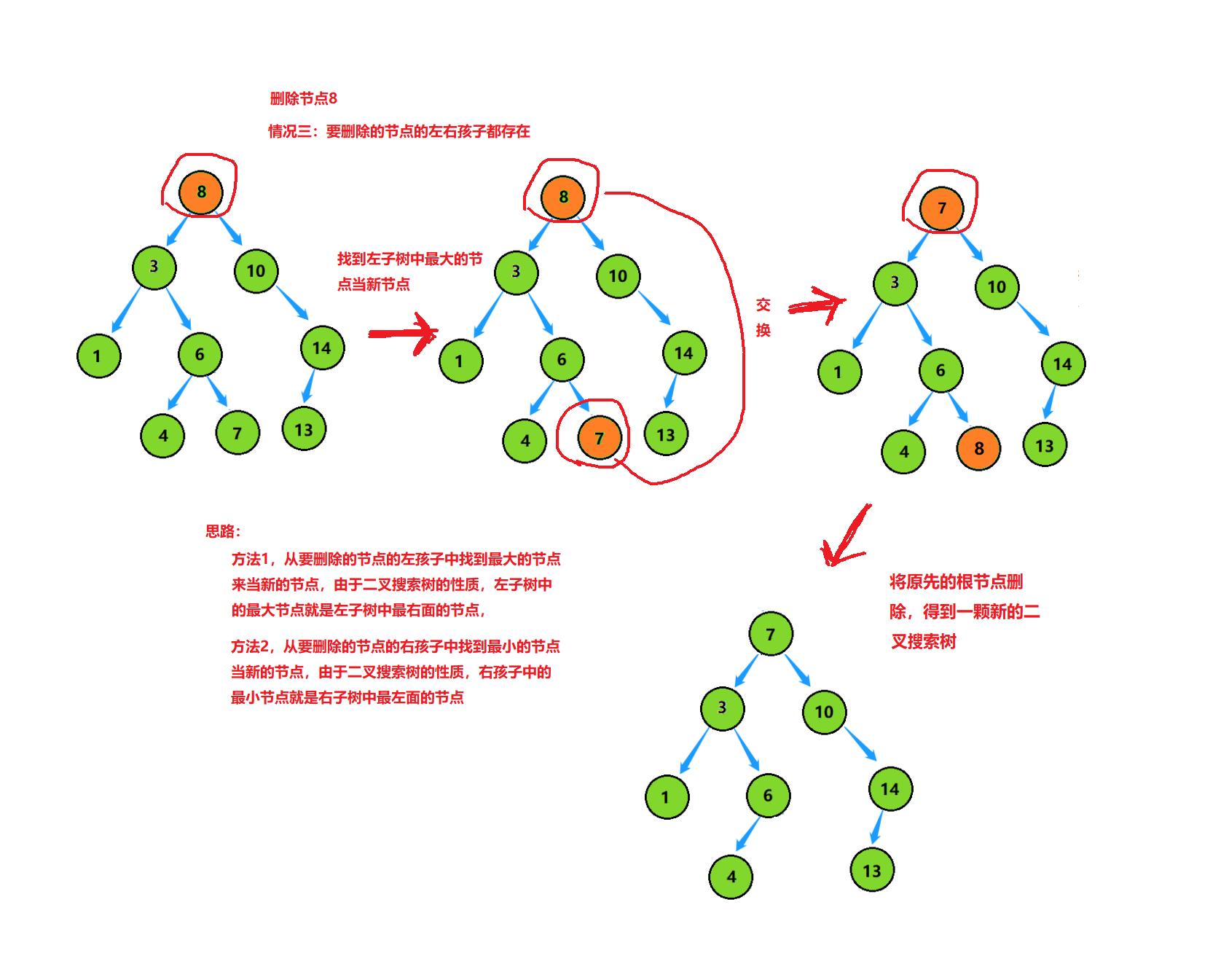
情况三:要删除的节点左右孩子都存在
bool Erase(const K& key)
{
//查找要删除的节点
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if(cur->_key>key)
{
parent = cur;
cur = cur->_left;
}
else {
//情况一:要删除的节点的左子树为空
if (cur->_left == nullptr)
{
//特殊情况,cur是根节点
if (cur == _root)
{
_root = cur->_right;
}
else {
if (cur == parent->_left)
{
parent->_left = cur->_right;
}
else if (cur == parent->_right)
{
parent->_right = cur->_right;
}
}
} //情况一:要删除的节点的右子树为空
else if (cur->_right == nullptr)
{
//特殊情况,cur是根节点
if (cur == _root)
{
_root = cur->_left;
}
else {
if (cur == parent->_left)
{
parent->_left = cur->_left;
}
else if (cur == parent->_right)
{
parent->_right = cur->_left;
}
}
}
else {
//左右子树都不为空
Node* parent = cur; //为防止交换后找不到该节点,所以要一起找到他的父节点
//找到左子树最大的值,也就是左子树最右边的值
Node* leftMax = cur->_left;
while(leftMax->_right)
{
parent = leftMax;
leftMax = leftMax->_right;
}
//将找到的适合做点的哪个值和要删除的值交换
swap(cur->_key, leftMax->_key);
//两种情况,找到的leftMax是parent的左孩子还是右孩子
if (leftMax == parent->_left)
{
//因为找的是最右边节点,所以他的右孩子为空,直接托孤
parent->_left = leftMax->_left;
}
else {
parent->_right = leftMax->_left;
}
cur = leftMax;//删除交换后的节点
}
delete cur;
return true;
}
}
//找完也没找到
return false;
}
遍历数据
二叉搜索树的一个特性,一个节点的所有左子树的值一定比这个节点的值小,一个节点的所有右子树的值比这个节点的值大,所以我们使用中序遍历可以得到一个升序的数组,我们实现的遍历也是利用递归实现中序遍历。
因为调用遍历需要传入根节点,而根节点数据是private类型的,不对外公开,所以我们可以再次封装一层函数用来调用遍历函数。
void InOrder()
{
_InOrder(_root);
cout << endl;
}
void _InOrder(Node* root)
{
if (root == nullptr)return;
_InOrder(root->_left);
cout << root->_key << " ";
_InOrder(root->_right);
}
源码
#pragma once
#include<iostream>
using namespace std;
template<class K>
//二叉搜索树的节点
struct BSTreeNode
{
struct BSTreeNode* _left;
struct BSTreeNode* _right;
K _key;
BSTreeNode(K key = K())
:_key(key)
,_left(nullptr)
,_right(nullptr)
{}
};
template<class K>
class BSTree
{
typedef BSTreeNode<K> Node;
public:
bool Insert(const K& key)
{
//判断特殊情况,如果根节点为空,则将要插入的元素作为根节点
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
//相同值,插入失败
return false;
}
}
cur = new Node(key);
if (parent->_key > key)parent->_left = cur;
else parent->_right = cur;
return true;
}
bool Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else {
return true;
}
}
return false;
}
bool Erase(const K& key)
{
//查找
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if(cur->_key>key)
{
parent = cur;
cur = cur->_left;
}
else {
//左为空
if (cur->_left == nullptr)
{
//特殊情况,cur是根节点
if (cur == _root)
{
_root = cur->_right;
}
else {
if (cur == parent->_left)
{
parent->_left = cur->_right;
}
else if (cur == parent->_right)
{
parent->_right = cur->_right;
}
}
}
else if (cur->_right == nullptr) //右为空
{
//特殊情况,cur是根节点
if (cur == _root)
{
_root = cur->_left;
}
else {
if (cur == parent->_left)
{
parent->_left = cur->_left;
}
else if (cur == parent->_right)
{
parent->_right = cur->_left;
}
}
}
else {
//左右子树都不为空
Node* parent = cur; //为防止交换后找不到该节点,所以要一起找到他的父节点
//找到左子树最大的值,也就是左子树最右边的值
Node* leftMax = cur->_left;
while(leftMax->_right)
{
parent = leftMax;
leftMax = leftMax->_right;
}
//将找到的适合做点的哪个值和要删除的值交换
swap(cur->_key, leftMax->_key);
//两种情况,找到的leftMax是parent的左孩子还是右孩子
if (leftMax == parent->_left)
{
//因为找的是最右边节点,所以他的右孩子为空,直接托孤
parent->_left = leftMax->_left;
}
else {
parent->_right = leftMax->_left;
}
cur = leftMax;//删除交换后的节点
}
delete cur;
return true;
}
}
//找完也没找到
return false;
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
void _InOrder(Node* root)
{
if (root == nullptr)return;
_InOrder(root->_left);
cout << root->_key << " ";
_InOrder(root->_right);
}
private:
Node* _root=nullptr;
};
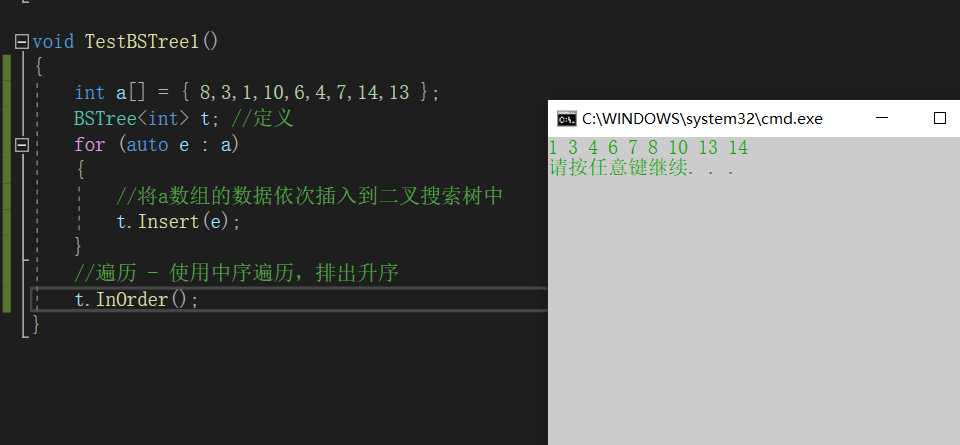
void TestBSTree1()
{
int a[] = { 8,3,1,10,6,4,7,14,13 };
BSTree<int> t; //定义
for (auto e : a)
{
//将a数组的数据依次插入到二叉搜索树中
t.Insert(e);
}
//遍历 - 使用中序遍历,排出升序
//t.InOrder();
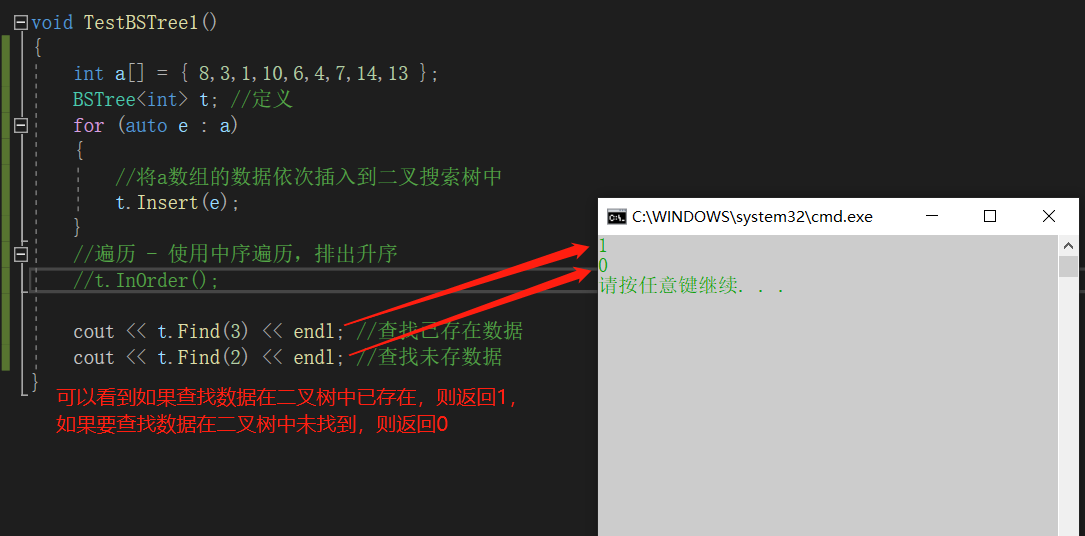
cout << t.Find(3) << endl; //查找已存在数据
cout << t.Find(2) << endl; //查找未存数据
}