pso优化bp网络机械故障诊断(MATLAB代码)

news2024/11/15 23:39:15

在混合算法中,需要优化的对象(粒子)是 BP 神经网络的权值和值。首先应把要优化的神经网络的全部权值和闽值构成一个实数数组,并赋予它们 [0,1之间的随机数。然后,按照选定的网络结构,用前向算法计算出对应于每组输入样本的神经网络输出。这里BP网络的激活函数都选为sigmoid 函数然后用改进PSO算法搜索出最优位置,使如下的均方误差指标(适应度函数值)达到最小:

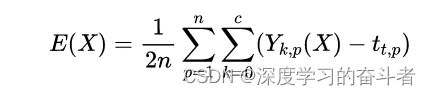
式中,n为样本个数;c 为网络神经元的输出个数;tkp为第p个样本的第个理想输出值;Y.p为第p个样本的第  个实际输出值。
这样适应度函数值达到最小时搜索到的便是 BP 网络的最佳权值和闻值。下面是混合算法的实现步骤:
(1)确定适应度权值w、最大允许迭代步数 t、搜索范围[-Xmax,Xmax]、最大速度，并根据网络规模确定粒子数。 

通过改进的粒子群算法对网络权值进行训练,改善了使用多层感知器的BP算中存在的网络学习收敛速度慢,以及容易陷入局部极小等问题,提高了网络收敛速度,可以有效地用于设备故障诊断,对设备故障进行特征识别和诊断分析。 

文件夹如下

 

数据集介绍

data5.m

训练集特征

训练集的标签 

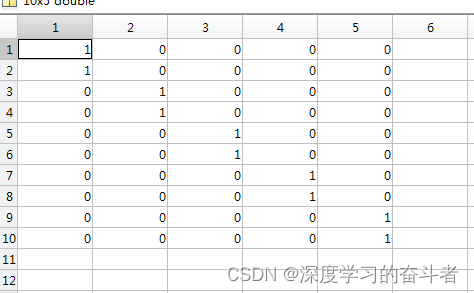
测试集的特征 

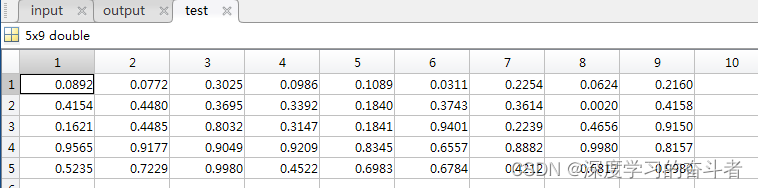 主程序（main.m文件）

%% 该代码为基于PSO和BP网络的预测
%% 初始化
clc
clear
warning off
%读取数据
load data5 input output test

%节点个数
inputnum=9;
hiddennum=13;
outputnum=5;

%训练数据和预测数据
input_train=input';
input_test=test';
output_train=output';
output_test=output';
inputn=input_train;
outputn=output_train;
%构建网络
dx=[0,1;0,1;0,1;0,1;0,1;0,1;0,1;0,1;0,1];
net=newff(dx,[hiddennum,outputnum],{'tansig' 'logsig'},'trainlm');

% 参数初始化
%粒子群算法中的两个参数
c1 = 1.49445;
c2 = 1.49445;

maxgen=100;   % 进化次数  
sizepop=20;   %种群规模

Vmax=1;
Vmin=-1;
popmax=5;
popmin=-5;

for i=1:sizepop
    pop(i,:)=5*rands(1,200);
    V(i,:)=rands(1,200);
    fitness(i)=fun(pop(i,:),inputnum,hiddennum,outputnum,net,inputn,outputn);
end
% 个体极值和群体极值
[bestfitness bestindex]=min(fitness);
zbest=pop(bestindex,:);   %全局最佳
gbest=pop;    %个体最佳
fitnessgbest=fitness;   %个体最佳适应度
fitnesszbest=bestfitness;   %全局最佳适应度

%% 迭代寻优
for i=1:maxgen    
    for j=1:sizepop   
        %速度更新
        V(j,:) = V(j,:) + c1*rand*(gbest(j,:) - pop(j,:)) + c2*rand*(zbest - pop(j,:));
        V(j,find(V(j,:)>Vmax))=Vmax;
        V(j,find(V(j,:)<Vmin))=Vmin;
        
        %种群更新
        pop(j,:)=pop(j,:)+0.2*V(j,:);
        pop(j,find(pop(j,:)>popmax))=popmax;
        pop(j,find(pop(j,:)<popmin))=popmin; 
        
        %自适应变异
        pos=unidrnd(21);
        if rand>0.95
            pop(j,pos)=5*rands(1,1);
        end      
        
        %适应度值
        fitness(j)=fun(pop(j,:),inputnum,hiddennum,outputnum,net,inputn,outputn);
    end    
    
    for j=1:sizepop
    %个体最优更新
    if fitness(j) < fitnessgbest(j)
        gbest(j,:) = pop(j,:);
        fitnessgbest(j) = fitness(j);
    end   
    
    %群体最优更新 
    if fitness(j) < fitnesszbest
        zbest = pop(j,:);
        fitnesszbest = fitness(j);
    end
    end    
    yy(i)=fitnesszbest;            
end

%% 结果分析
plot(yy)
title(['适应度曲线  ' '终止代数＝' num2str(maxgen)]);
xlabel('进化代数');ylabel('适应度');
x=zbest;

%% 把最优初始阀值权值赋予网络预测
% %用pso优化的BP网络进行值预测
w1=x(1:inputnum*hiddennum);
B1=x(inputnum*hiddennum+1:inputnum*hiddennum+hiddennum);
w2=x(inputnum*hiddennum+hiddennum+1:inputnum*hiddennum+hiddennum+hiddennum*outputnum);
B2=x(inputnum*hiddennum+hiddennum+hiddennum*outputnum+1:inputnum*hiddennum+hiddennum+hiddennum*outputnum+outputnum);
net.iw{1,1}=reshape(w1,hiddennum,inputnum);
net.lw{2,1}=reshape(w2,outputnum,hiddennum);
net.b{1}=reshape(B1,hiddennum,1);
net.b{2}=reshape(B2,outputnum,1);

%% BP网络训练
%网络进化参数
net.trainParam.epochs=1000;
net.trainParam.lr=0.001;
net.trainParam.goal=1e-6;
net.trainParam.showwindow = 0;

%网络训练
[net,per2]=train(net,inputn,outputn);

%% BP网络预测
an=sim(net,input_test)

pso.m文件 

clc
clear
warning off
%读取数据
load data5 input output test

%节点个数
inputnum=9;
hiddennum=13;
outputnum=5;

%训练数据和预测数据
input_train=input';
input_test=test';
output_train=output';
output_test=output';
inputn=input_train;
outputn=output_train;
%构建网络
dx=[0,1;0,1;0,1;0,1;0,1;0,1;0,1;0,1;0,1];
net=newff(dx,[hiddennum,outputnum],{'tansig' 'logsig'},'trainlm');

% 参数初始化
%粒子群算法中的两个参数
c1 = 1.49445;
c2 = 1.49445;

maxgen=2;   % 进化次数  
sizepop=20;   %种群规模

Vmax=1;
Vmin=-1;
popmax=5;
popmin=-5;

for i=1:sizepop
    pop(i,:)=5*rands(1,200);
    V(i,:)=rands(1,200);
    fitness(i)=fun(pop(i,:),inputnum,hiddennum,outputnum,net,inputn,outputn);
end
% 个体极值和群体极值
[bestfitness bestindex]=min(fitness);
zbest=pop(bestindex,:);   %全局最佳
gbest=pop;    %个体最佳
fitnessgbest=fitness;   %个体最佳适应度值
fitnesszbest=bestfitness;   %全局最佳适应度值

%% 迭代寻优
for i=1:maxgen    
    for j=1:sizepop   
        %速度更新
        V(j,:) = V(j,:) + c1*rand*(gbest(j,:) - pop(j,:)) + c2*rand*(zbest - pop(j,:));
        V(j,find(V(j,:)>Vmax))=Vmax;
        V(j,find(V(j,:)<Vmin))=Vmin;
        
        %种群更新
        pop(j,:)=pop(j,:)+0.2*V(j,:);
        pop(j,find(pop(j,:)>popmax))=popmax;
        pop(j,find(pop(j,:)<popmin))=popmin; 
        
        %自适应变异
        pos=unidrnd(21);
        if rand>0.95
            pop(j,pos)=5*rands(1,1);
        end      
        
        %适应度值
        fitness(j)=fun(pop(j,:),inputnum,hiddennum,outputnum,net,inputn,outputn);
    end    
    
    for j=1:sizepop
    %个体最优更新
    if fitness(j) < fitnessgbest(j)
        gbest(j,:) = pop(j,:);
        fitnessgbest(j) = fitness(j);
    end   
    
    %群体最优更新 
    if fitness(j) < fitnesszbest
        zbest = pop(j,:);
        fitnesszbest = fitness(j);
    end
    end    
    yy(i)=fitnesszbest;            
end

%% 结果分析
plot(yy)
title(['适应度曲线  ' '终止代数＝' num2str(maxgen)]);
xlabel('进化代数');ylabel('适应度');
x=zbest;

%% 把最优初始阀值权值赋予网络预测
% %用遗传算法优化的BP网络进行值预测
w1=x(1:inputnum*hiddennum);
B1=x(inputnum*hiddennum+1:inputnum*hiddennum+hiddennum);
w2=x(inputnum*hiddennum+hiddennum+1:inputnum*hiddennum+hiddennum+hiddennum*outputnum);
B2=x(inputnum*hiddennum+hiddennum+hiddennum*outputnum+1:inputnum*hiddennum+hiddennum+hiddennum*outputnum+outputnum);
net.iw{1,1}=reshape(w1,hiddennum,inputnum);
net.lw{2,1}=reshape(w2,outputnum,hiddennum);
net.b{1}=reshape(B1,hiddennum,1);
net.b{2}=reshape(B2,outputnum,1);

%% BP网络训练
%网络进化参数
net.trainParam.epochs=1000;
net.trainParam.lr=0.001;
net.trainParam.goal=1e-6;
net.trainParam.showwindow = 0;

%网络训练
[net,per2]=train(net,inputn,outputn);

%% BP网络预测
an=sim(net,input_test)

 效果图

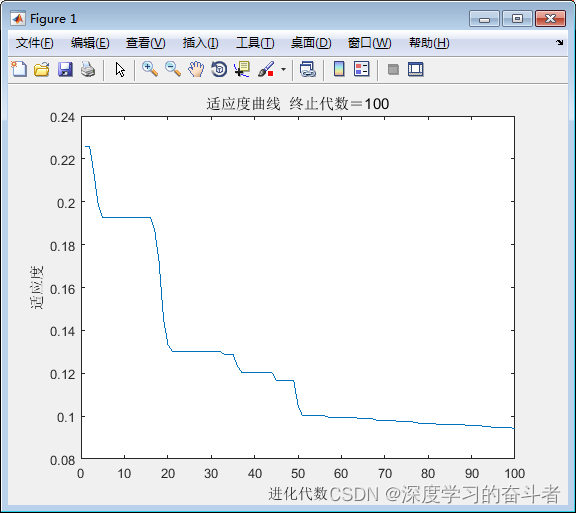
测试集的预测标签

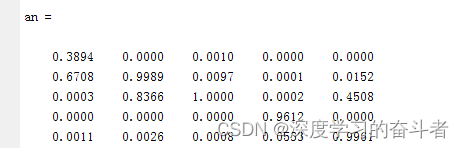
完整代码可以关注

 

function error = fun(x,inputnum,hiddennum,outputnum,net,inputn,outputn)
% 该函数用来计算适应度
%x          input     个体
%inputnum   input     输入层节点数
%outputnum  input     隐含层节点数
%net        input     网络
%inputn     input     训练输入数据
%outputn    input     训练输出数据

%error      output    个体适应度

%提取
w1=x(1:inputnum*hiddennum);
B1=x(inputnum*hiddennum+1:inputnum*hiddennum+hiddennum);
w2=x(inputnum*hiddennum+hiddennum+1:inputnum*hiddennum+hiddennum+hiddennum*outputnum);
B2=x(inputnum*hiddennum+hiddennum+hiddennum*outputnum+1:inputnum*hiddennum+hiddennum+hiddennum*outputnum+outputnum);

 
%网络权值赋值
net.iw{1,1}=reshape(w1,hiddennum,inputnum);
net.lw{2,1}=reshape(w2,outputnum,hiddennum);
net.b{1}=reshape(B1,hiddennum,1);
net.b{2}=reshape(B2,outputnum,1);
%可以关注https://mbd.pub/o/bread/ZJyTmZZt

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/806359.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【unity细节】怎么让物体产生碰撞后不会被撞飞，但是有碰撞停止的效果

【unity细节】怎么让物体产生碰撞后不会被撞飞，但是有碰撞停止的效果

&#x1f468;‍&#x1f4bb;个人主页&#xff1a;元宇宙-秩沅 hallo 欢迎 点赞&#x1f44d; 收藏⭐ 留言&#x1f4dd; 加关注✅! 本文由 秩沅 原创 收录于专栏&#xff1a;unity细节和bug ⭐怎么让物体产生碰撞后不会被撞飞&#xff0c;但是有碰撞停止的效果⭐ 文章目录…
阅读更多...
PHP-Mysql图书管理系统--【白嫖项目】

PHP-Mysql图书管理系统--【白嫖项目】

强撸项目系列总目录在000集 PHP要怎么学–【思维导图知识范围】 文章目录 本系列校训本项目使用技术 首页phpStudy 设置导数据库后台的管理界面数据库表结构项目目录如图&#xff1a;代码部分&#xff1a;主页的head 配套资源作业&#xff1a; 本系列校训 用免费公开视频&am…
阅读更多...
Linux安装Kafka图形化界面

Linux安装Kafka图形化界面

Apache Kafka本身是一个分布式的消息系统&#xff0c;它并没有官方提供的图形界面。Kafka主要通过命令行界面进行管理和操作。 如果你需要一个可视化的界面来管理Kafka&#xff0c;可以考虑安装一些第三方的Kafka管理工具&#xff0c;例如Kafdrop、Kafka Manager或Conduktor等…
阅读更多...
NOAUTH Authentication required解决方法

NOAUTH Authentication required解决方法

执行redis报错如下&#xff1a; 提示需要进行权限认证 解决方案 输入redis密码 格式&#xff1a; auth 密码
阅读更多...
vue使用Clodop插件打印

vue使用Clodop插件打印

一、前往lodop官网&#xff0c;下载插件&#xff0c;http://www.lodop.net/index.html 这里下载的window64位的&#xff0c;将插件安装好&#xff0c;运行&#xff0c;会看到 点击‘去了解C-Lodop>>’,会跳转至使用说明页面&#xff0c;在这个页面里&#xff0c;可以打印…
阅读更多...
Facebook开源PySlowFast视频理解代码库

Facebook开源PySlowFast视频理解代码库

近年来&#xff0c;Facebook 人工智能研究&#xff08;FAIR&#xff09;一直在为视频理解研究做出重大贡献。在2019年10月的ICCV上&#xff0c;该团队推出了一个基于Python的代码库PySlowFast。FAIR现在是开源的PySlowFast&#xff0c;还有一个预先训练的模型库&#xff0c;并承…
阅读更多...
camunda流程引擎简单上手

camunda流程引擎简单上手

快速开始 参考官方的文档&#xff1a; https://docs.camunda.org/get-started/ 我下面会在关键部署简单记录一下。 下载 服务端 https://docs.camunda.org/manual/latest/installation/full/tomcat/pre-packaged/ 为了方便我们直接下载tomcat整合包&#xff0c;不用自己在…
阅读更多...
1200*C. K-th Not Divisible by n

1200*C. K-th Not Divisible by n

Example input 6 3 7 4 12 2 1000000000 7 97 1000000000 1000000000 2 1 output 10 15 1999999999 113 1000000001 1 解析&#xff1a; 将每 n 个数看成一组&#xff0c;每组缺少了一个n的倍数&#xff0c;所以按照对 n-1 整除和取模分别得出组数和余数&#xff0c;乘起来…
阅读更多...
Hexo+GithubPages免费搭建个人博客网站

Hexo+GithubPages免费搭建个人博客网站

HexoGithubPages免费搭建个人博客网站 目录 一、前言二、Github配置 新建同名仓库配置Pages 三、安装Hexo四、配置hexo-deployer-git五、访问六、发布文章七、安装主题 一、前言 我之前开了好几年的云服务器了&#xff0c;实际上使用场景并不是很多&#xff0c;感觉有点浪费…
阅读更多...
Android Studio手动下载安装SDK，图文详解

Android Studio手动下载安装SDK，图文详解

本教程适用于手动下载Android SDK&#xff0c;适合第一次安装Android Studio的同学&#xff0c;进入安卓SDK网址&#xff1a;https://www.androiddevtools.cn/。首先你需要在D盘新建一个目录Android SDK&#xff0c;存放后面下载的工具。 1、下载SDK Tools&#xff0c;解压到An…
阅读更多...
【机器学习 | 朴素贝叶斯】朴素贝叶斯算法：概率统计方法之王，简单有效的数据分类利器

【机器学习 | 朴素贝叶斯】朴素贝叶斯算法：概率统计方法之王，简单有效的数据分类利器

&#x1f935;‍♂️ 个人主页: AI_magician &#x1f4e1;主页地址&#xff1a; 作者简介&#xff1a;CSDN内容合伙人&#xff0c;全栈领域优质创作者。 &#x1f468;‍&#x1f4bb;景愿&#xff1a;旨在于能和更多的热爱计算机的伙伴一起成长&#xff01;&#xff01;&…
阅读更多...
微信读书：长期投资（阅读摘录）

微信读书：长期投资（阅读摘录）

微信读书&#xff1a;长期投资&#xff08;阅读摘录&#xff09; 所有投资高手的时间精力都投向了这三大块&#xff1a;行动、思考、读书。 我们把耐心发挥到了极致&#xff0c;这正是价值投资的关键特征之一。 通常在牛市中想要跑赢大盘&#xff0c;难度非常大。 实际上&am…
阅读更多...
C语言每日一题：8.除自身以外数组的乘积。

C语言每日一题：8.除自身以外数组的乘积。

题目&#xff1a; 题目&#xff1a; 思路一&#xff1a; &#xff08;先不考虑题目的要求循序渐进的方法&#xff09; 1.动态开辟数组&#xff0c;初始化数组内容为全1. 2.使用双for循环去给answer赋值。 3.在相同位置不去*对应的下标位置的数组值&#xff0c;而是*1&#xff…
阅读更多...
【Linux命令200例】lsattr用于查看文件或目录的属性

【Linux命令200例】lsattr用于查看文件或目录的属性

&#x1f3c6;作者简介&#xff0c;黑夜开发者&#xff0c;全栈领域新星创作者✌&#xff0c;2023年6月csdn上海赛道top4。 &#x1f3c6;本文已收录于专栏&#xff1a;Linux命令大全。 &#x1f3c6;本专栏我们会通过具体的系统的命令讲解加上鲜活的实操案例对各个命令进行深入…
阅读更多...
测试开源C#人脸识别模块ViewFaceCore（5：质量检测和眼睛状态检测）

测试开源C#人脸识别模块ViewFaceCore（5：质量检测和眼睛状态检测）

ViewFaceCore模块中的FaceQuality支持预测人脸质量&#xff0c;最初以为是预测人体体重&#xff0c;实际测试过程中才发现是评估人脸图片质量&#xff0c;主要调用Detect函数执行图片质量检测操作&#xff0c;其函数原型如下所示&#xff1a; //// 摘要:// 人脸质量评估///…
阅读更多...
tf卡为什么显示0字节？tf卡显示0字节怎么恢复数据

tf卡为什么显示0字节？tf卡显示0字节怎么恢复数据

我的TF卡现在显示字节为0&#xff0c;想要打开总是会弹出要求格式化的对话框&#xff0c;里面有我重要的数据。请问如何恢复里面的数据啊&#xff1f;急&#xff01;急&#xff01;急&#xff01; ——在日常使用中&#xff0c;我们可能将重要的数据存储在TF卡中。然而&#x…
阅读更多...
【每天40分钟，我们一起用50天刷完 (剑指Offer)】第四十天 40/50【二叉树递归】

【每天40分钟，我们一起用50天刷完 (剑指Offer)】第四十天 40/50【二叉树递归】

专注 效率 记忆 预习 笔记 复习 做题 欢迎观看我的博客&#xff0c;如有问题交流&#xff0c;欢迎评论区留言&#xff0c;一定尽快回复&#xff01;&#xff08;大家可以去看我的专栏&#xff0c;是所有文章的目录&#xff09; 　 文章字体风格&#xff1a; 红色文字表示&#…
阅读更多...
【雕爷学编程】Arduino动手做（175）---机智云ESP8266开发板模块3

【雕爷学编程】Arduino动手做（175）---机智云ESP8266开发板模块3

37款传感器与执行器的提法&#xff0c;在网络上广泛流传&#xff0c;其实Arduino能够兼容的传感器模块肯定是不止这37种的。鉴于本人手头积累了一些传感器和执行器模块&#xff0c;依照实践出真知&#xff08;一定要动手做&#xff09;的理念&#xff0c;以学习和交流为目的&am…
阅读更多...
flask中的蓝图

flask中的蓝图

flask中的蓝图 在 Flask 中&#xff0c;蓝图&#xff08;Blueprint&#xff09;是一种组织路由和服务的方法&#xff0c;它允许你在应用中更灵活地组织代码。蓝图可以大致理解为应用或者应用中的一部分&#xff0c;可以在蓝图中定义路由、错误处理程序以及静态文件等。然后可以…
阅读更多...
vcruntime140_1.dll无法继续执行代码重新安装方法

vcruntime140_1.dll无法继续执行代码重新安装方法

cruntime140_1.dll是Windows操作系统中的一个动态链接库文件&#xff0c;它包含了一些与C运行时相关的函数和资源。在Windows系统中&#xff0c;许多应用程序和游戏都依赖于vcruntime140_1.dll文件来正常运行。当系统中缺少或损坏了vcruntime140_1.dll文件时&#xff0c;就会出…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023