引言
打算写写树形数据结构:二叉查找树、红黑树、跳表和 B 树。这些数据结构都是为了解决同一个基本问题:如何快速地对一个大集合执行增删改查。
本篇是第一篇,讲讲搜索树的基础:二叉搜索树。
基本问题
如何在一千万个手机号中快速找到 13012345432 这个号(以及相关联信息,如号主姓名)?
最笨的方案
把一千万个手机号从头到尾遍历一遍,直到找到该手机号,返回对应的姓名。其时间复杂度是 O(n)————当然这肯定不是我们要的方案。
最秀的方案
用散列表,可以在 O(1) 的时间复杂度完成查找。
关于散列表的原理和代码参见 算法(TypeScript 版本)。
散列表的问题
散列表的查询性能非常优秀,插入和删除的性能也不赖,但它有什么问题呢?
我们稍微变换一下问题:如何在一千万个手机号中快速找到在 1301111111 到 13022222222 之间所有的手机号?
和基本问题不同的是,这是个范围查询。
散列表的本质是通过对关键字(本例中是手机号)执行 hash 运算,将其转换为数组下标,进而可以快速访问。
此处讲的数组是 C 语言意义上的数组,不是 javascript、PHP 等脚本语言中的数组。C 语言的数组是一段连续的内存片段,对数组元素的访问是通过内存地址运算进行的,可在常数时间内访问数组中任意元素。
hash 运算的特点是随机性,这也带来了无序性,我们无法保证 hash(1301111111) < hash(1301111112)。
无序性使得我们无法在散列表上快速执行范围查找,必须一个一个比较,时间复杂度又降到 O(n)。
基于有序数组的二分搜索
如果这一千万的手机号是排好序的(升序),我们有没有更好的办法实现上面的范围查找呢?
对于排好序的序列,我们如果能快速找到下限(1301111111)和上限(13022222222)所在的位置,那么两者之间所有的手机号就都是符合条件的。
如何才能快速找到 1301111111 的位置呢?
想想我们是怎么玩猜数字游戏的?
第一次猜 100,发现大了,第二次我们便倾向于猜 50 附近的数————而不是猜 99,如图:
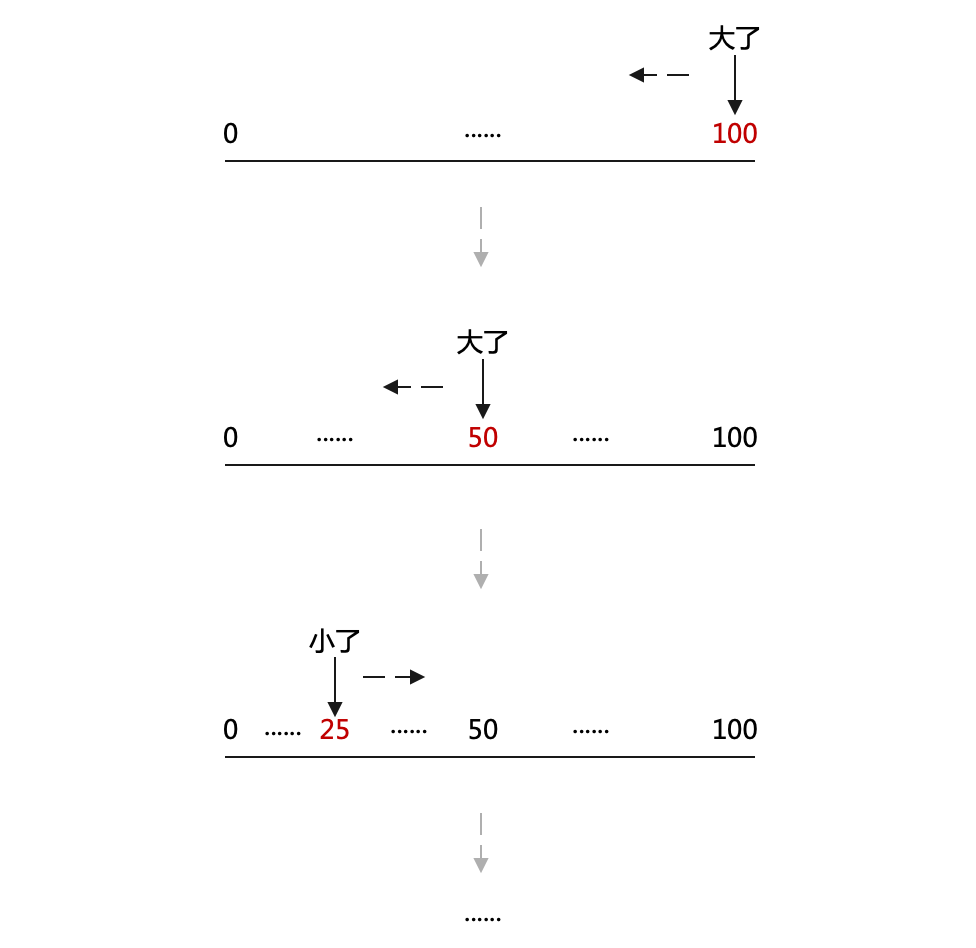
这种思想叫二分法————这种方法可以将问题范围成倍地缩小,进而可以至多尝试 log2nlog2n 次即可找出解。对于一千万个手机号来说,至多只需要比较 24 次即可找出 1301111111 的位置。相比于一千万次,简直是天壤之别。
代码如下:
interface Value {
// 为方便起见,这里限定 key 是数值类型
key: number;
val: unknown;
}
/**
* 二分搜索
* @param arr - 待搜索数组,必须是按升序排好序的(根据 Value.key)
* @param key - 搜索关键字
* @reutrn 搜索到则返回对应的 Value,否则返回 null
*/
function binSearch(arr: Value[], key: number): Value | null {
if (arr.length === 0) {
return null
}
// 子数组左右游标
let left = 0
let right = arr.length - 1
while (left <= right) {
// 取中
const mid = left + Math.floor((right - left) / 2)
const val = arr[mid]
if (key === val.key) {
return val
}
// key 小于 val 则在左边找
if (key < val.key) {
right = mid - 1
} else {
left = mid + 1
}
}
return null
}
所以,如果需要对这一千万个手机频繁地执行范围查找,二分搜索法是个不错的选择:先对一千万个手机号执行排序,然后对排好序的序列执行二分搜索。
二分搜索的问题
二分搜索能很快地执行精确查找和范围查找,但它仍然存在问题。
对一百个元素执行二分搜索,必须能够在常数时间内定位到第 50 个元素————只有数组(C 语言意义上的)这种数据结构才能做到。
也就是说,必须用数组来实现二分搜索。
但数组有个很大的缺陷:对插入和删除操作并不友好,它们都可能会造成数组元素迁移。
比如要往有序数组 arr = [1, 2, 3, 4, 5 ..., 100] 中插入元素 0 且继续保证数组元素的有序性,则必须先将既有的一百个元素都往右移一位,然后将 0 写到 arr[0] 位置。删除元素则会造成后续元素的左移。
倘若插入和删除操作非常频繁,这种迁移(复制)操作会带来很大的性能问题。
可见,对有序数组的查询可以在 O(log2nlog2n) 执行,但其写操作却是 O(n) 复杂度的。
有没有什么数据结构能够让读写操作都能在 O(log2nlog2n) 内完成呢?
二分搜索的启发
二分搜索的优势是能够在一次操作中将问题范围缩小到一半,进而能够在对数的时间复杂度上求得问题的解。不过其劣势是依赖于数组,因而其插入和删除性能低下。
那么,我们现在的目的便是解决二分搜索的写(插入和删除)性能。
要想提高写性能,我们的直觉是摆脱数组这种数据结构的桎梏————是否有别的数据结构代替数组?
一个很自然的想法是链表。链表的优势在于其元素节点之间是通过指针关联的,这使得插入和删除元素时只需要变更指针关系即可,无需实际迁移数据。
// 链表的节点定义
interface Node {
data: Value;
next: Node;
}
然而,链表的劣势是查询:它无法像数组那样通过下标访问(而只能从头节点一个一个遍历访问),进而也就无法实现二分法。
如对于数组 arr = [1, 2, 3, 4, 5],我们能直接通过 arr[2] 访问中间元素;但对于链表 link = 1 -> 2 -> 3 -> 4 -> 5,由于不是连续内存地址,无法通过下标访问,只能从头开始遍历。
那么,我们如何解决链表的查询问题呢?或者说如何用链表来模拟有序数组的二分法呢?
二分法有两个操作:
- 取中。快速定位到中间位置的元素(对于有序序列来说就是中位数)。
- 比较。根据第一步取得的元素,决定后续操作:如果相等则返回;如果比目标大,则取左半部子集继续操作;如果比目标小,则取右半部子集继续操作。
那么,如何在链表上实现上面两个操作?
我们先考虑操作二:比较。如果比较结果不相等,则会去左边或者右边继续查找。我们可以改造一下链表节点,用左右指针来表示“左边”和“右边”,左右指针分别指向左子链表和右子链表。改造后的节点定义如下:
// 改进的节点定义
interface Node {
data: Value;
// 左指针
left: Node;
// 右指针
right: Node;
}
由于改造后的链表节点有 left 和 right 两个指针,相当于一个节点分了两个叉,故名为二叉。
再考虑操作一:取中。取中将原数组一分为三:当前元素(中间元素)、左子数组、右子数组。
我们可以将它映射到改造后的链表中的当前节点、左(left)子链表、右(right)子链表。查找时,如果当前节点的值小于目标值,则通过 right 指针进入到右子链表中继续查找,反之通过 left 指针进入左子链表查找。
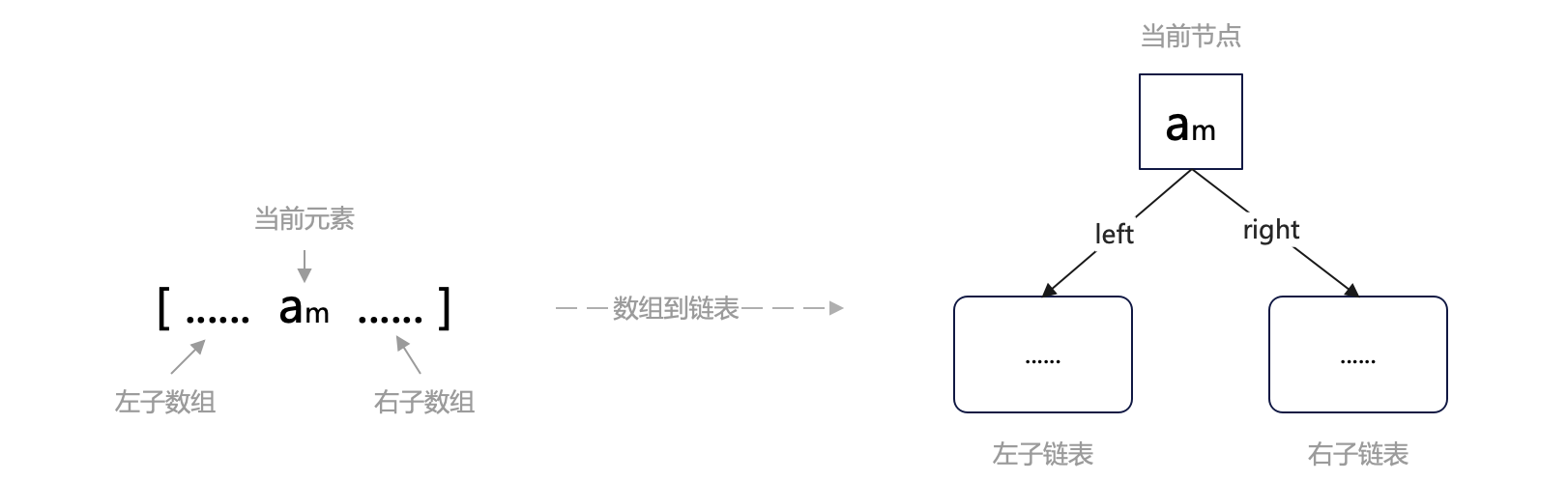
继续分析之前,我们先从直观上考察一下改造后的链表。分叉后,整个结构不再像单条链子,更像一棵树,于是我们不再称之为“二叉链表”,而是称作“二叉树”。对应地,左右子链表也更名为“子树”。
对应数组看,很容易知道,节点左子树中的所有元素都小于等于节点元素,右子树中的所有元素都大于等于节点元素————这是二叉搜索树最重要(甚至是唯一重要)的性质。
至此,我们用链表的节点代替数组的元素,用节点的左右指针(或者说左右指针指向的两棵子树)代替左右子数组。
现在还剩下最后一个问题:如何将数组中的每个元素映射到这棵二叉搜索树(或者叫“改造后的链表”)中?
既然二分法是不断地取数组(包括左右子数组)中间位置的元素进行比较,那么我们将取出来的元素从上到下(从树根开始)依次挂到这棵树的节点上即可,如此当我们从树根开始遍历时,拿到的元素的顺序便和从数组中拿到的一致。
我们以数组 arr = [1, 2, 3, 4, 5, 6, 7] 为例,看看如何生成对应的二叉搜索树。
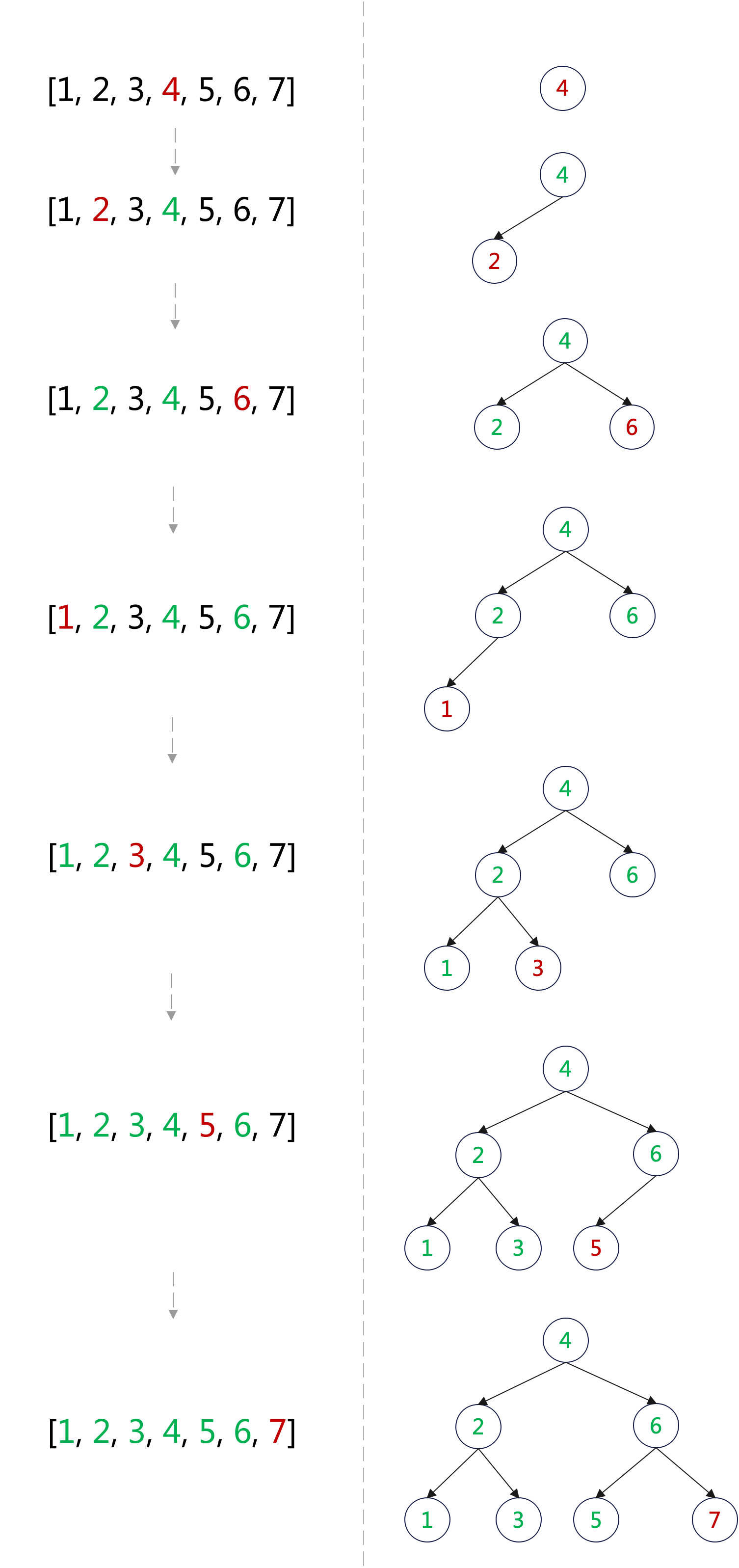
如上图:
- 先取整个数组中间元素 4,作为二叉树的根节点;
- 取左子数组的中间元素 2,作为根节点的左子节点;
- 取右子数组的中间元素 6,作为根节点的右子节点;
- 依此递归处理,直到取出数组中所有的元素生成二叉树的节点,整棵二叉树生成完成;
我们将上面的过程转换成代码:
// 二叉搜索树
class BinSearchTree {
// 树根节点
root: Node;
}
/**
* 基于已排好序(根据 key)的数组 arr 构建平衡的二叉搜索树
*/
function buildFromOrderdArray(arr: Value[]): BinSearchTree {
const tree = new BinSearchTree()
// 从树根开始构建
tree.root = innerBuild(arr, 0, arr.length - 1)
return tree
}
/**
* 基于子数组 arr[start:end] 构建一棵以 node 为根节点的二叉子树,返回根节点 node
*/
function innerBuild(arr: Value[], start: number, end: number): Node {
if (start > end) {
// 空
return null
} else if (start == end) {
// 只剩下一个元素了,则直接返回一个节点
return { data: arr[start], left: null, right: null }
}
/**
* 使用二分思想构建二叉树
*/
// 中间元素
const mid = start + Math.floor((end - start) / 2)
// 当前节点
const curr: Node = { data: arr[mid], left: null, right: null }
/**
* 递归生成左右子树
*/
// 左子树
curr.left = innerBuild(arr, start, mid - 1)
// 右子树
curr.right = innerBuild(arr, mid + 1, end)
return curr
}
二叉搜索树的查找
二叉搜索树是基于二分搜索思想构建的,其搜索逻辑也和二分搜索相同,只不过将左右子数组替换成左右子树。
以搜索元素 13 为例:
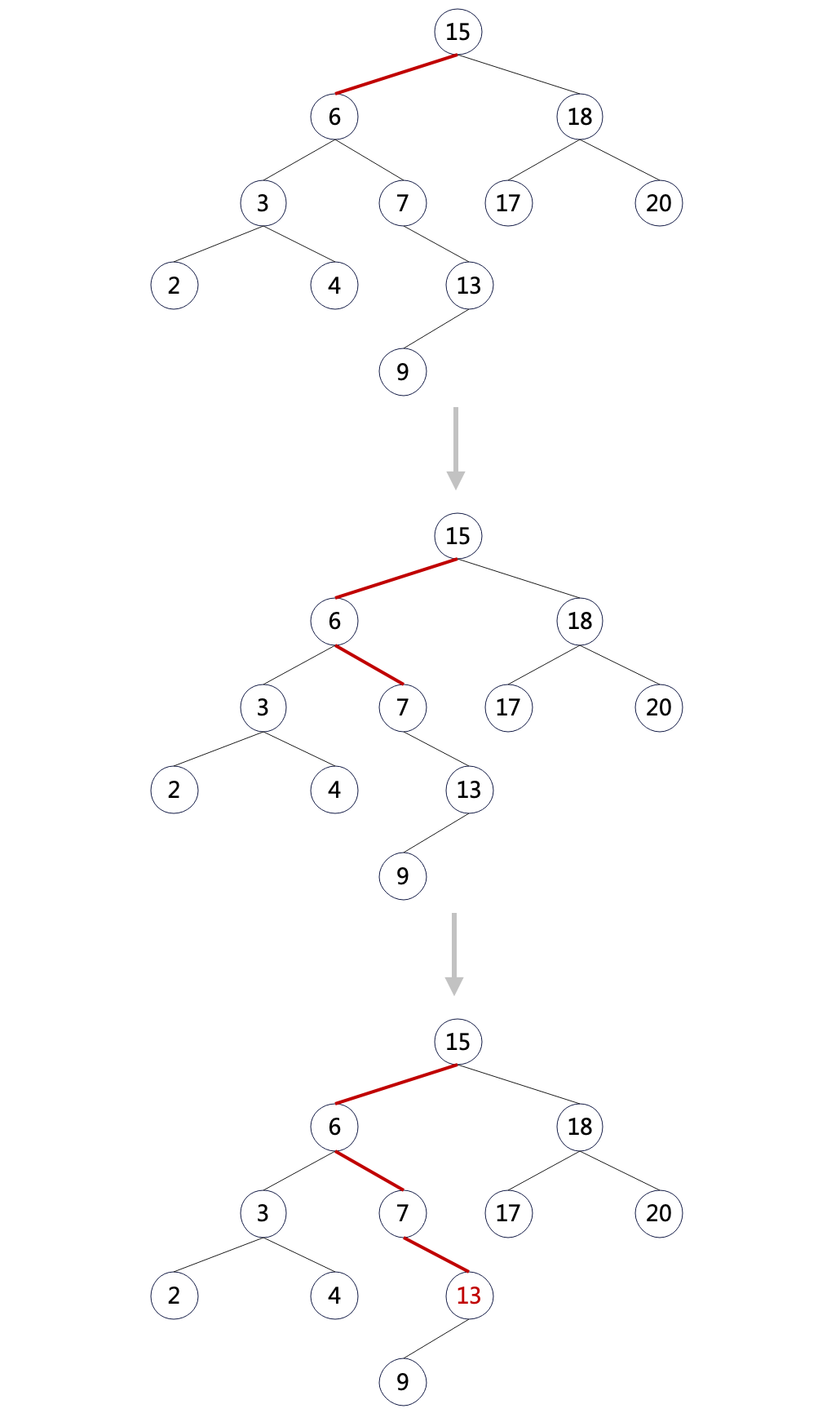
上图中搜索步骤:
- 从根节点开始比较,15 大于 13,到本节点的左子树继续搜索;
- 节点 6 小于 13,到本节点的右子树继续搜索;
- 节点 7 小于 13,到本节点的右子树继续搜索;
- 节点 13 等于 13,找到目标节点,结束;
对比二分搜索可以发现,二叉搜索树中的 left 和 right 子树就是对应二分搜索中左右子数组,两者的搜索逻辑本质上是一致的。
代码如下:
class BinSearchTree {
// 树根节点
root: Node;
/**
* 在以 node 为根的子树中搜索关键字为 key 的节点并返回该节点
* 如果没有找到则返回 null
*/
search(key: unknown, node: Node = undefined): Node {
// 默认取根
node = node === undefined ? this.root : node
// 遇到 null 节点,说明没搜到,返回 null
if (!node) {
return null
}
// 先判断当前节点
if (node.data.key === key) {
// 找到,即可返回
return node
}
// 没有找到,则视情况继续搜索左右子树
if (key < node.data.key) {
// 目标值小于当前节点,到左子树中搜索
return this.search(key, node.left)
}
// 目标值大于等于当前节点,到右子树中搜索
return this.search(key, node.right)
}
}
从图中可见,对于任何元素的搜索,搜索次数不可能大于从根到所有叶节点的最长路径中节点个数(上图中是 5)。如果用这条路径的边来表达的话,搜索次数不可能超过最长路径边数加 1。
这个最长路径的边数即是整棵树的高。
对于一颗完美的平衡二叉树来说,这个高 h = log2nlog2n,其中 n 是节点数量。因而说二叉搜索树的查询时间复杂度是 O(log2nlog2n),和二分搜索是一致的。
注意上面说的是完美的平衡二叉树,但二叉搜索树并不是天生平衡的,所以才引出了各种平衡方案,诸如 2-3 树、红黑树、B 树等。
特殊查找:最小元素
由于二叉搜索树中的任意一个节点,其左边元素总小于该节点,所以要找最小元素,就是从根节点开始一直往左边找。
如图:
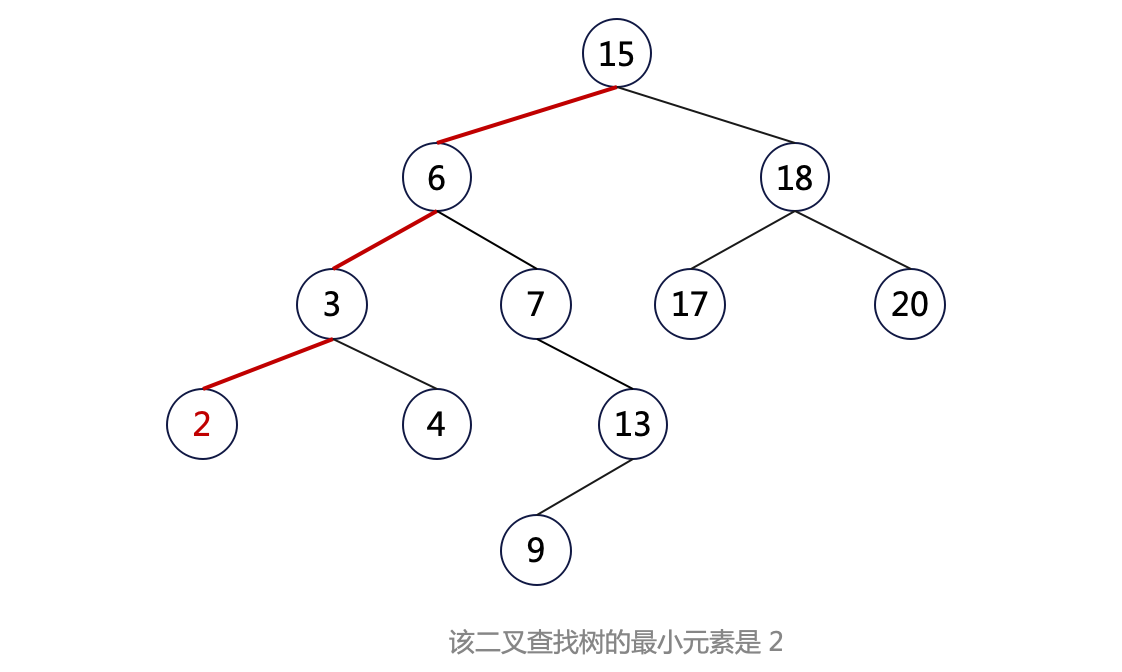
代码如下:
class BinSearchTree {
// 树根节点
root: Node;
/**
* 查找以 node 为根的子树的最小节点并返回
*/
min(node: Node = undefined): Node {
// 默认取根节点
node = node === undefined ? this.root : node
if (node === null || !node.left) {
// 如果是空子树,或者 node.left 是空节点,则返回
return node
}
// 存在左子树,继续往左子树中找
return this.min(node.left)
}
}
相对应的是最大值,也就是递归地往右边找,此处略。
按序遍历
对于有序数组,很容易通过循环从头到尾按序遍历数组中元素,对应地,如何按序遍历二叉搜索树呢?
二叉搜索树是根据二分法递归生成的,所以同样可以用二分法来解决此问题。
对于一棵树来说,它分为三部分:树根节点、左子树、右子树,其中大小关系是:左子树 <= 树根节点 <= 右子树,所以我们以这个顺序遍历整棵树,便可以按序输出。
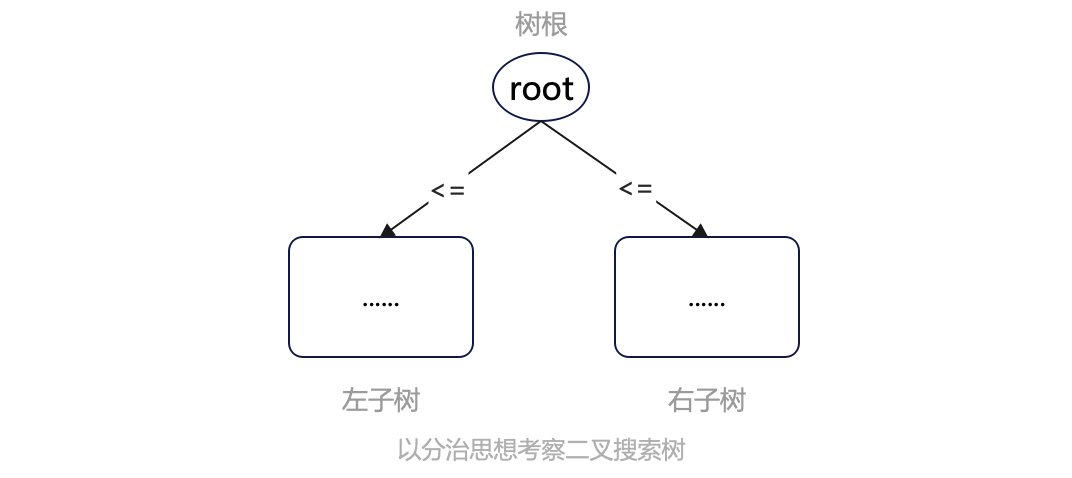
这种遍历方式,由于是在中间步骤操作树根节点,又称之为中序遍历。
相应地,按“树根节点 -> 左子树 -> 右子树”的顺序遍历称之为先序遍历,按“左子树 -> 右子树 -> 树根节点”的顺序遍历称之为后序遍历。
中序遍历代码:
class BinSearchTree {
// 树根节点
root: Node;
/**
* 中序遍历
*/
inorder(): Node[] {
const arr: Node[] = []
this.innerInorder(this.root, arr)
return arr
}
/**
* 对 x 子树执行中序遍历,遍历的节点放入 arr 中
*/
innerInorder(x: Node, arr: Node[]) {
if (!x) {
return
}
// 先遍历左子树
this.innerInorder(x.left, arr)
// 自身
arr.push(x)
// 右子树
this.innerInorder(x.right, arr)
}
}
范围查询
如何在二叉搜索树上执行范围查询?
问题:按序返回二叉搜索树中所有大于等于 start 且小于等于 end 的节点集合(即返回所有节点 x,x 满足:start <= x <= end)。
上面的中序遍历其实就是一种特殊的范围查询:min <= x <= max。所以范围查询的思路和中序遍历一样,只不过在遍历时加上范围限制。
具体来说,什么时候需要去查左子树呢?当左子树有可能存在符合条件的元素时需要去查。如果当前节点 x 的值小于范围下限(start),而 x 的左子树的值都小于等于 x 的,说明此时其左子树中不可能存在符合条件的节点,无需查询;或者,如果 x 的值大于范围上限(end),而 x 的右子树的值都大于等于 x 的,说明此时其右子树中不可能存在符合条件的节点,也无需查询。其他情况则需要查询。
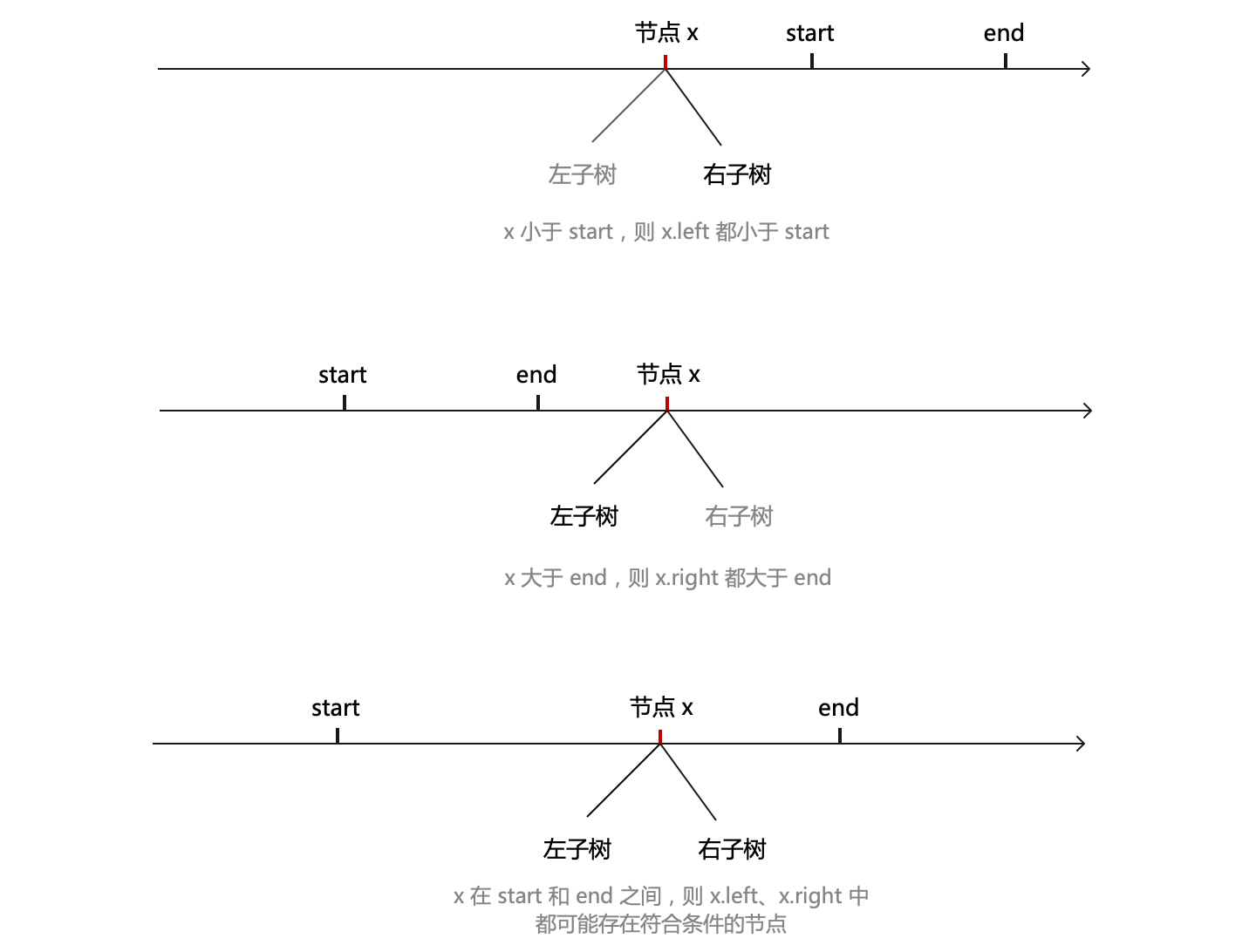
代码如下:
class BinSearchTree {
// 树根节点
root: Node;
/**
* 按序返回所有大于等于 start 且小于等于 end 的节点集合
*/
range(start: unknown, end: unknown): Node[] {
const arr: Node[] = []
this.innerRange(this.root, start, end, arr)
return arr
}
/**
* 在 x 子树中查找所有大于等于 start 且小于等于 end 的节点并放入 arr 中
*/
innerRange(x: Node, start: unknown, end: unknown, arr: Node[]) {
if (!x) {
return
}
// 比较节点 x 和 start、end 之间的大小关系
const greaterThanStart = x.data.key >= start
const smallerThanEnd = x.data.key <= end
// 如果当前节点大于等于 start,则需要搜索其左子树
if (greaterThanStart) {
this.innerRange(x.left, start, end, arr)
}
// 如果 x 在 start 和 end 之间,则符合条件,存入 arr
if (greaterThanStart && smallerThanEnd) {
arr.push(x)
}
// 如果当前节点小于等于 end,则需要搜索其右子树
if (smallerThanEnd) {
this.innerRange(x.right, start, end, arr)
}
}
}
插入操作
对于二叉树来说,新节点总是被插入到 null 节点(末端)处。
还是以上图为例,插入新节点 14:
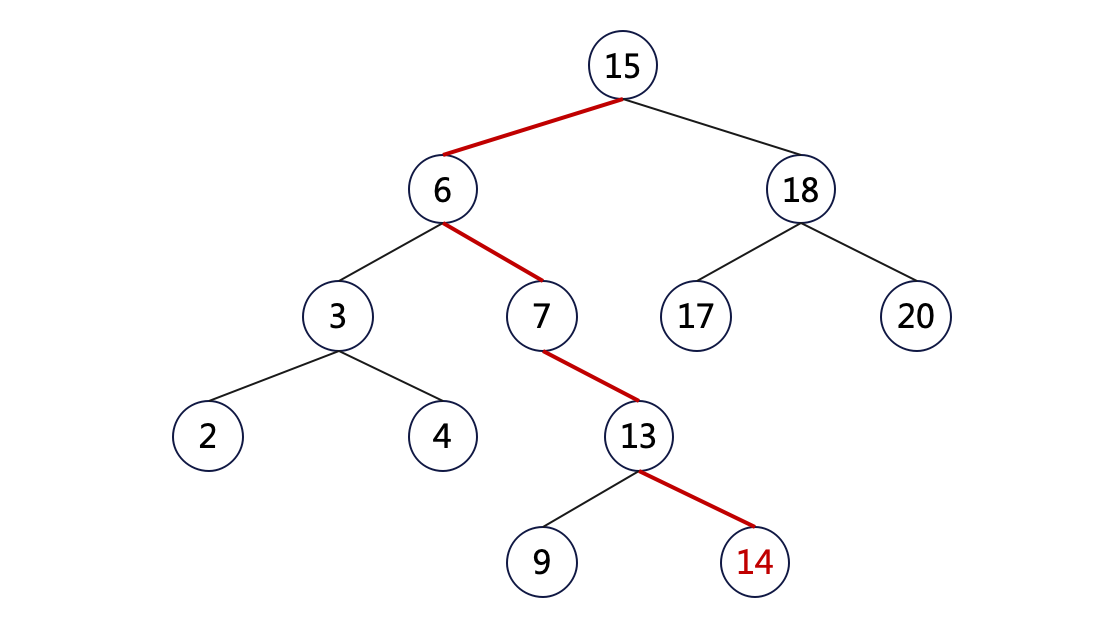
如图所示,插入操作分两步:
- 搜索。这一步和查找操作一样,相当于是搜索这个新节点 14,结果没搜到,遇到了 null 节点(Node(13).right);
- 插入。生成新节点 14 并插入到节点 13 的右侧(Node(13).right = Node(14));
很明显,插入操作的时间复杂度也是 O(log2nlog2n),完美!
插入操作的代码如下:
class BinSearchTree {
// 树根节点
root: Node;
/**
* 将元素 data 插入到树中
*/
insert(data: Value) {
// 从根节点开始处理
// 插入完成后,将新根赋值给 root
this.root = this.innerInsert(data, this.root)
}
/**
* 将元素 data 插入到以 node 为根的子树中
* 返回插入元素后的子树的根节点
*/
innerInsert(data: Value, node: Node): Node {
if (node === null) {
// 遇到了 null 节点,说明需要插入到该位置
return { data: data, left: null, right: null }
}
// 比较 data 和 node 的值,视情况做处理
if (data.key < node.key) {
// 待插入的元素小于当前节点,需要插入到当前节点的左子树中
node.left = this.innerInsert(data, node.left)
} else {
// 插入到右子树中
node.right = this.innerInsert(data, node.right)
}
// 插入完成后,需返回当前节点
return node
}
}
删除操作
删除操作需要分几种情况。
情况一:删除叶子节点,该节点的 left 和 right 都是 null。
这种情况很简单,直接删掉该元素即可。如删除节点 9:
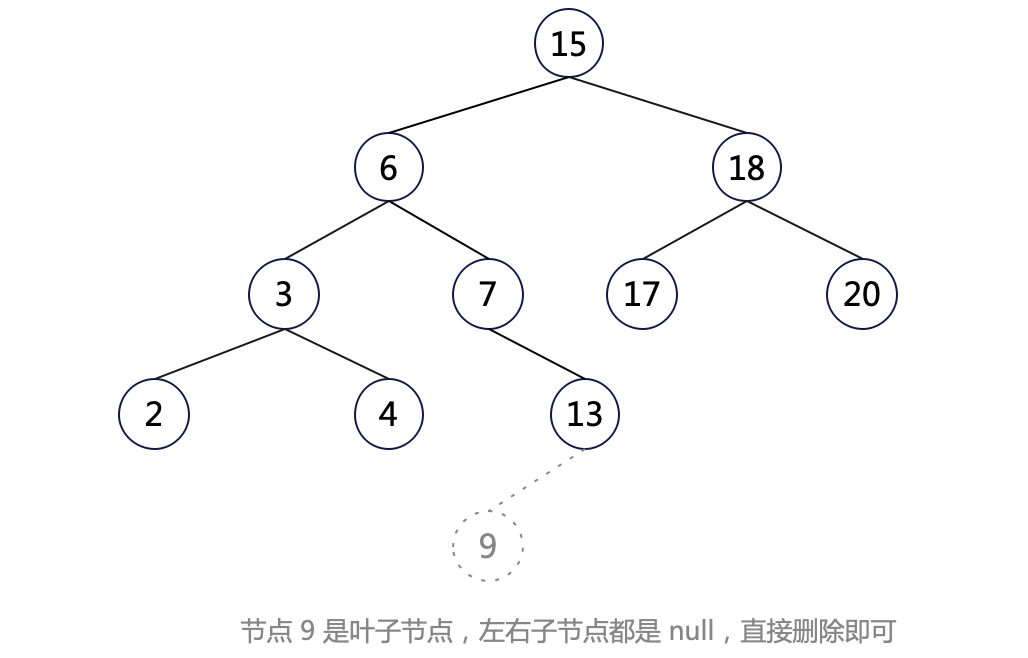
情况二:待删除的节点只有一个子节点,用该子节点代替该节点即可。如删除节点 13:
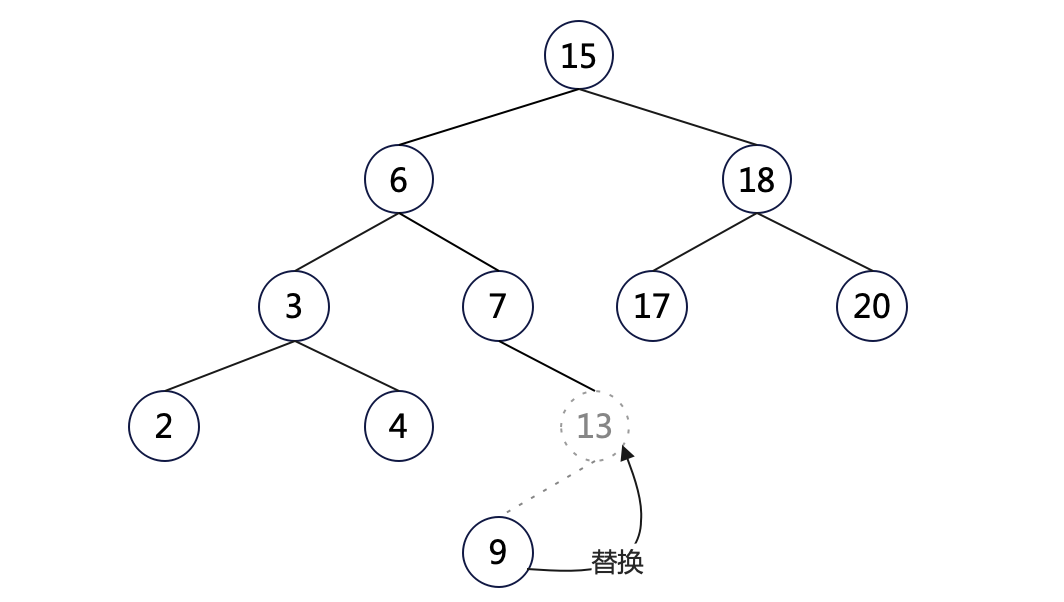
以上两种情况都比较简单,第三种情况则稍微复杂。
情况三:待删除的节点有左右两个子节点。如图中节点 6。将 6 删除后,我们无法简单的用其 left 或 right 子节点替代它————因为这会造成两棵子树一系列的变动。
前面说过,二叉搜索树本质上是由有序数组演化而来,那么我们不妨以数组的角度看是否有所启示。
上图用数组表示:arr = [2, 3, 4, 6, 7, 9, 13, 15, 18, 17, 20]。该数组中删掉元素 6 后,如何才能让数组中其他元素调整次数最少(这里不考虑迁移,因为二叉树不存在迁移开销)?
自然是直接用 6 的前一个(4)或者后一个(7)元素替代 6 的位置。其中 4 恰恰是 6 左边子数组中的最大值,而 7 恰恰是其右边子数组中的最小值。
我们不妨用右边子数组中最小值(7)来替代 6————映射到二叉搜索树中便是节点 6 的右子树的最小节点。
前面已经讨论过二叉搜索树中最小值的求解逻辑:顺着节点左子树(left)一直递归查找,直到 node.left 等于 null,该 node 便是最小值————也就是说,一棵树的最小节点不可能有左子节点,即最小节点最多有一个子节点,这便是情况一或者情况二。
那么能否用右子树中最小节点(7)替代当前节点(6)呢?无论从有序数组还是从二叉搜索树本身角度看,都很容易证明是可以的(替换后仍然符合二叉搜索树的性质)。
因而,情况三可以作如下处理:
- 将右子树中最小节点的 data 赋值给当前节点;
- 删除右子树中最小节点;
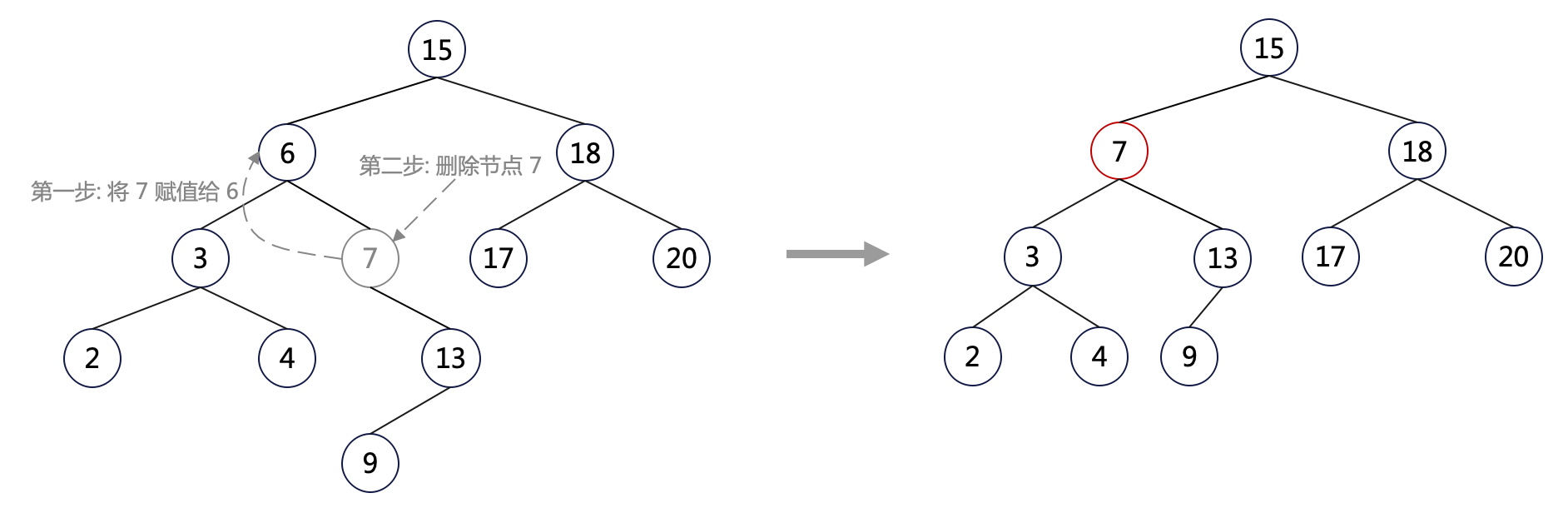
代码如下:
class BinSearchTree {
// 树根节点
root: Node;
// ...
/**
* 删除 key 对应的节点
*/
delete(key: unknown) {
const node = this.search(key, this.root)
if (!node) {
// key 不存在
return
}
this.root = this.innerDelete(this.root, node)
}
/**
* 删除子树 current 中 del 节点,并返回操作完成后的子树根节点
*/
innerDelete(current: Node, del: Node): Node {
/**
* 当前节点即为待删除节点
*/
if (current === del) {
// 情况一:当前节点没有任何子节点,直接删除
if (!current.left && !current.right) {
return null
}
// 情况二:只有一个子节点
if (current.left && !current.right) {
// 只有左子节点,用左子节点替换当前节点
return current.left
}
if (current.right && !current.left) {
// 只有右子节点,用右子节点替换当前节点
return current.right
}
// 情况三:有两个子节点
// 取右子树的最小节点
const minNode = this.min(current.right)
// 用最小节点的值替换当前节点的
current.data = minNode.data
// 删除右子树中的最小节点
current.right = this.innerDelete(current.right, minNode)
return current
}
/**
* 当前节点不是待删除节点,视情况递归从左或右子树中删除
*/
if (del.data.key < current.data.key) {
// 待删除节点小于当前节点,从左子树删除
current.left = this.innerDelete(current.left, del)
} else {
// 待删除节点大于当前节点,继续从右子树删除
current.right = this.innerDelete(current.right, del)
}
return current
}
}
很容易证明,删除操作的时间复杂度也是 O(log2nlog2n)。
二叉搜索树的问题
由上面的插入操作可知,二叉搜索树新增节点时总是往末端增加新节点,这种操作方式有个问题:当我们一直朝同一个方向(一直向左或者一直向右)插入时,便很容易出现倾斜。
比如我们向一棵空树中依次插入 1, 2, 3, 4, 5:
const tree = new BinSearchTree()
tree.insert({ key: 1, val: 1 })
tree.insert({ key: 2, val: 2 })
tree.insert({ key: 3, val: 3 })
tree.insert({ key: 4, val: 4 })
tree.insert({ key: 5, val: 5 })
得到的二叉树如下:
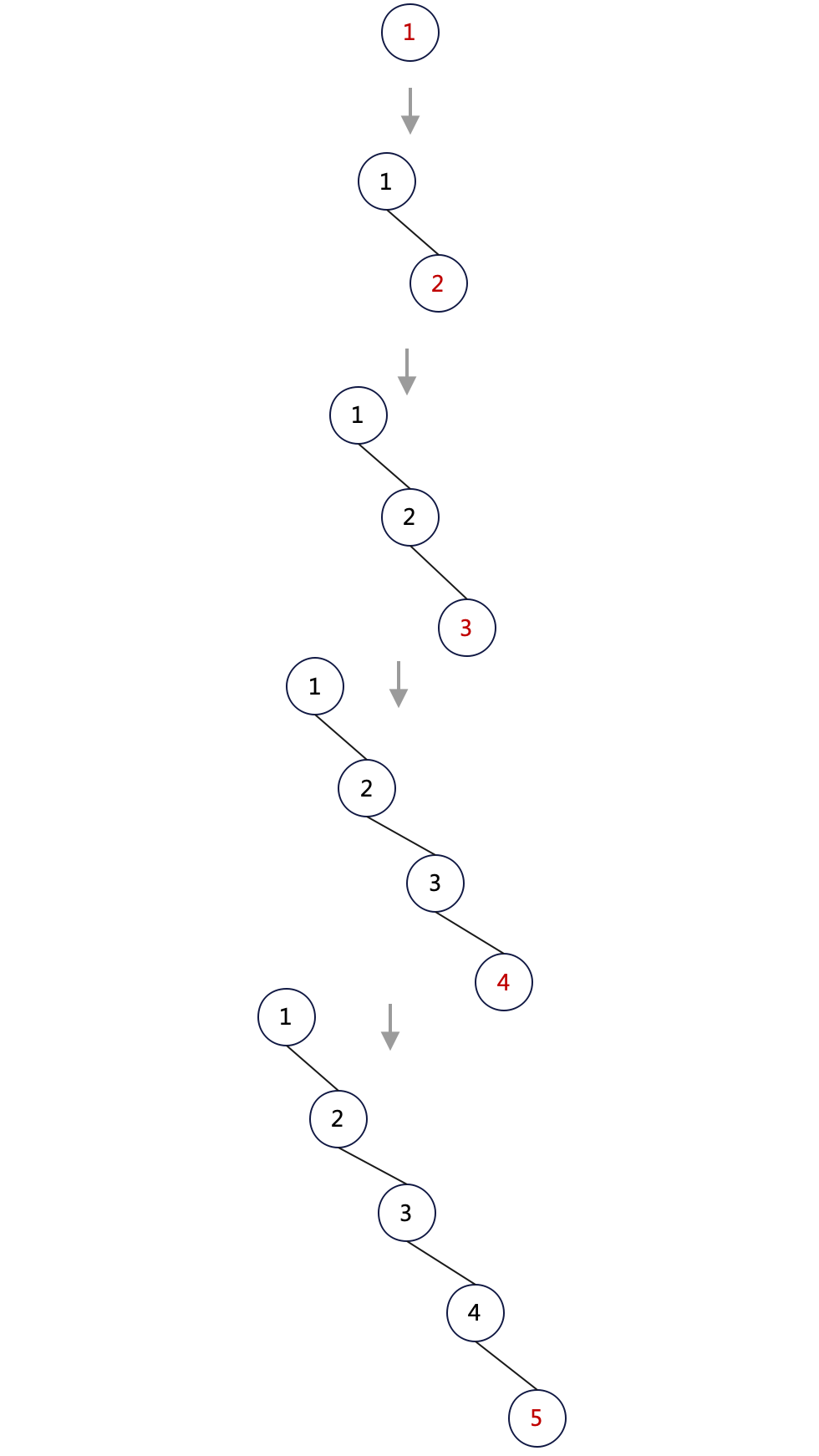
二叉树退化成了普通链表,所有的操作退化为 O(n) 复杂度!
所以在插入和删除二叉树节点时,需要执行额外的操作来维护树的平衡性,后面将要介绍的红黑树和 B 树就是两种非常著名的解决方案。
总结
- 散列表能很好地解决精确查询(O(1) 复杂度),但无法解决范围查询(必须 O(n) 复杂度);
- 基于有序数组的二分搜索能很好地解决精确查询和范围查询(O(log2nlog2n) 复杂度),但无法解决插入和删除(必须 O(n) 复杂度);
- 基于二分搜索思想改进的链表(二叉搜索树)能很好地解决查询(包括范围查询)、插入和删除,所有的操作都是 O(log2nlog2n) 的时间复杂度;
- 二叉搜索树中以任意节点作为根的子树仍然是一棵二叉搜索树,这个特点很重要,它是递归操作的关键;
- 二叉搜索树存在节点倾斜问题,会降低操作性能,极端情况下会退化成普通链表,所有的操作都退化到 O(n) 复杂度;
- 为解决二叉搜索树的倾斜问题,实际应用中需引入相关平衡方案,本系列的后序文章将介绍三种常见的方案:红黑树、跳表和 B 树;