指令调度（Instruction Scheduling）

news2025/1/11 2:44:15

指令调度（Instruction Scheduling）

指令调度的约束
基本机器模型
基本块调度
全局调度

指令调度是为了提高指令级并行（ILP），对于超长指令字（VLIW, Very Long Instruction Word）和多发射系统，ILP是可以有效提高硬件利用率。

指令调度的约束

指令调度也是一种程序的优化pass，需要遵循以下约束：

数据依赖约束。调度后代码执行结果需要和调度前相同。
控制依赖约束。所有调度前程序执行的指令都必须在调度后的程序中执行。
资源约束。调度不能超过机器上的资源。

数据依赖包括真依赖、反依赖、输出依赖和输入依赖，相关概念可以参阅数据依赖和控制依赖 Data Dependence and Contol Dependence。前3种依赖约束了指令的执行顺序，但其中只有真依赖的依赖关系是不可解除的，而反依赖和输出依赖都可以通过使用不同的变量来解除依赖关系。

一个基本块（BB）内指令只要满足数据依赖就可以进行任意重新排序，但基本块内的程序通常都很少，重排提升并行性非常有限。提高基本块之间的并行性就至关重要了。基本块间指令的调度需要遵循控制依赖的约束，如果指令a的结果决定了指令b是否执行，则称指令b控制依赖于指令a。控制依赖相关概念可以参阅数据依赖和控制依赖 Data Dependence and Contol Dependence。

资源约束是显而易见的，调度肯定不能超过机器物理资源的限制。

基本机器模型

在介绍指令调度前，先假设下我们的基本机器模型：

对于一个基本数学运算：

需要一个ALU单元的物理资源
需要一个时钟（clock）的时间

对于Loads (LD) 和 Stores (ST)：

需要一个MEM（Memory buffer）单元的物理资源
ST需要一个时钟时间。LD需要两个时钟时间才能完成，但是我们可以在下一个时钟ST到相同的内存位置，并且每个LD可以在任意时钟发射。

基本块调度

先从最简单的基本块调度说起，这里介绍列表调度（list scheduling）的方法。基本块内的指令顺序其实就是一种拓扑排序，基本块调度的目的是找到一种性能最佳（并行度最高）的拓扑排序。

一个基本块内的指令构建一个数据依赖图（data-dependece graph）：

节点就是基本块内的每条指令
边代表两条指令间的数据依赖， $i\rightarrow j$ 表示指令 $j$ 数据依赖于指令 $i$
边上有一个表示延迟的标号。代表目的指令必须在源指令发射后至少多少个时钟之后发射

例如：

LD r1, a          // MEM
LD r2, b          // MEM
ADD r3, r1, r2    // ALU
ST a r2           // MEM
ST b r1           // MEM
ST c r3           // MEM

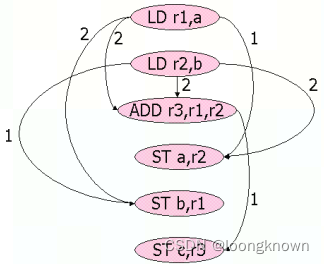
数据依赖图为：

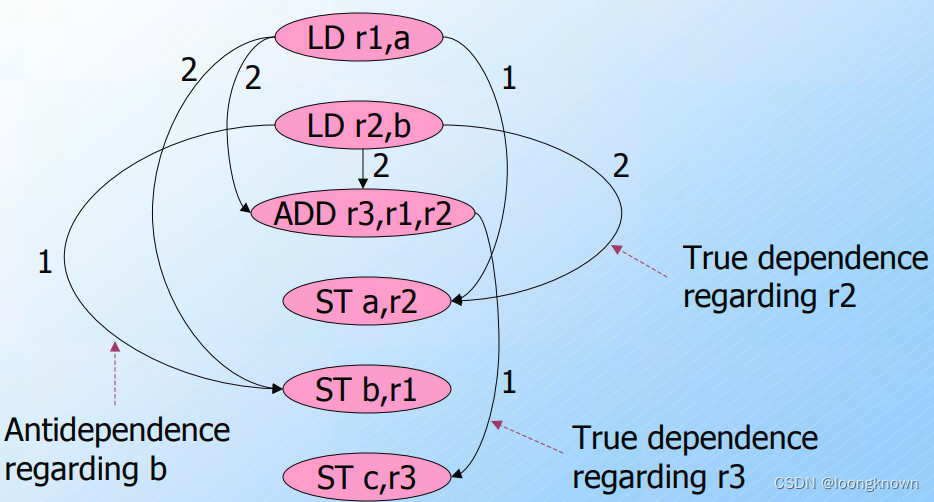
列表调度是一种简单的启发式的方法，在遵从数据依赖的基础上，选择一个带有优先级的拓扑排序来访问数据依赖图中的每个节点，比如启发式地先选择具有最长路径的节点。

指令选择的优先级：

最长路径（或关键路径）。从该节点开始的最长路径长度
满足资源限制
源指令的顺序

列表调度算法为：

使用列表调度算法对上述指令调度如下：

1）首先将 LD r1, a 和 LD r2, b加入到READY中，此时 READY={LD r1, a; LD r1, a}。则先调度第一条指令 LD r1, a，此时MEM资源限制，LD r2, b延迟到第二个时钟调度：

LD r1, a // clock 1  
LD r2, b // clock 2

此时更新READY为 READY={ADD r3, r1, r2; ST a r2; ST b r1 }。

2）接着ADD r3, r1, r2有最高优先权（最长执行路径），并且ALU资源可用，最早可以在第四个时钟调度：

LD r1, a    // clock 1      
LD r2, b    // clock 2

ADD r3, r1, r2  // clock 4

此时更新READY为 READY={ST a r2; ST b r1; ST c r3 }。

3）接着ST a r2有最高调度优先权，最早在时钟4就绪，并且MEM资源可用，因而可以调度到时钟4的位置：

LD r1, a    // clock 1      
LD r2, b    // clock 2

ADD r3, r1, r2      ST a r2   // clock 4

此时更新READY为 READY={ST b r1; ST c r3 }。

4）此时ST b r1有最高调度优先权，最早在时钟3就绪，并且MEM资源可用，因而可以调度到时钟3的位置：

LD r1, a    // clock 1      
LD r2, b    // clock 2
ST b r1     // clock 3
ADD r3, r1, r2      ST a r2   // clock 4

此时更新READY为 READY={ST c r3 }。

5）最后调度ST c r3，结果如下：

LD r1, a     // clock 1      
LD r2, b     // clock 2
ST b r1      // clock 3
ADD r3, r1, r2      ST a r2   // clock 4
ST c r3      // clock 5

全局调度

基本块可以调度的空间非常有限，因而跨基本块的全局调度至关重要。在介绍全局调度前，这里先介绍一个概念：控制等价的（control equivalent）。

如果基本块B支配基本块B’，并且基本块B’反向支配基本块，则称B和B‘是控制等价的。

假设每个时钟可以执行任意两条指令，除了加载指令需要两个时钟周期的延迟外，其余每条指令执行延迟为一个时钟周期。下面的例子，假设a、b、c、d和e地址各不相同，并且它们的地址分别存放在R1～R5中。

通过观察，有以下几个优化点：

不管分支如何跳转，B3中的指令都会被执行，一次B3可以和B1并行执行。
B2和B1存在控制依赖关系，可以投机性地执行B2中的加载指令，如果B2被执行则可以节省两个时钟周期。但保存指令不能投机性地执行，它会覆盖某个内存位置上的值，却可以延迟执行一个保存指令。

移动后的代码可以在4个时钟周期内完成。

指令移动的目的是在遵从数据依赖的同时增加指令的并行性。包括向上代码移动和向下代码移动。

向上代码移动：将指令从基本块src向上移动到基本块dst：

如果src和dst是控制等价的，如果这样的移动没有破坏数据依赖关系，并且可以让的代码运行的更快，这样的移动没有任何问题。
如果src不反向支配dst，则意味着存在一条经过dst但不经过src的路径，在这条路径上会多执行一条被移动过去的指令。首先这条被移动的指令必须是没有副作用的，否则这样的移动就是非法移动。如果这条指令在dst中是”免费“执行的（利用的是闲置的物理资源），则这样的移动不会产生开销。当控制流达到src时，这次移动就是有收益的。
如果dst不支配src，则存在一条不经过dst就到达src的路径，那我们需要在这条路径上插入被移动指令的拷贝（补偿代码）。补偿代码会让某些执行路径变慢，因此需要对这种移动的收益作出评估才行。

向下代码移动：将指令从基本块src向下移动到基本块dst。根据支配情况也同样有以上类似问题。

这里介绍一个基本的全局调度算法——区域调度，它优先调度最内层循环，并且仅向上移动代码。

程序可以被看作是一个 区域（Region） 的层次结构。区域是流图中只有单个入口节点的部分，正式地讲，一个区域是满足如下条件的节点N和边E的集合：

N中有一个支配N中所有节点的头节点h。
如果某个节点m可以不经过h可以到达N中的n，那么m也在N中。
E是N中任意两个节点n1和n2之间的控制流边的集合。有些进入h的边（可能）不在其中。

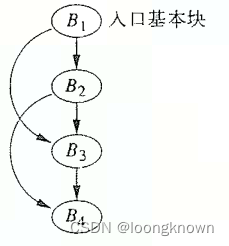
B1和B2以及边B1->B2形成一个区域。B1、B2和B3以及边B1->B2、B2->B3和B1->B3也形成一个区域。但是B2、B3以及边B2->B3组成的子图不是一个区域。