title: 传染病模型
date: 2023-7-24 10:55:00
updated: 2023-7-24 10:55:00
tags:
- 算法
- 数学建模
- 传染病模型
- matlab
categories: 数学建模
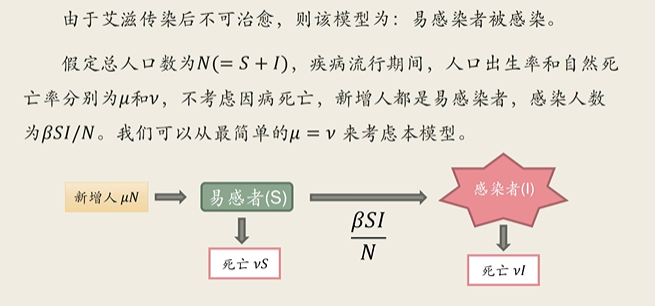
传染病模型中的符号表示


SI模型(艾滋传染模型)
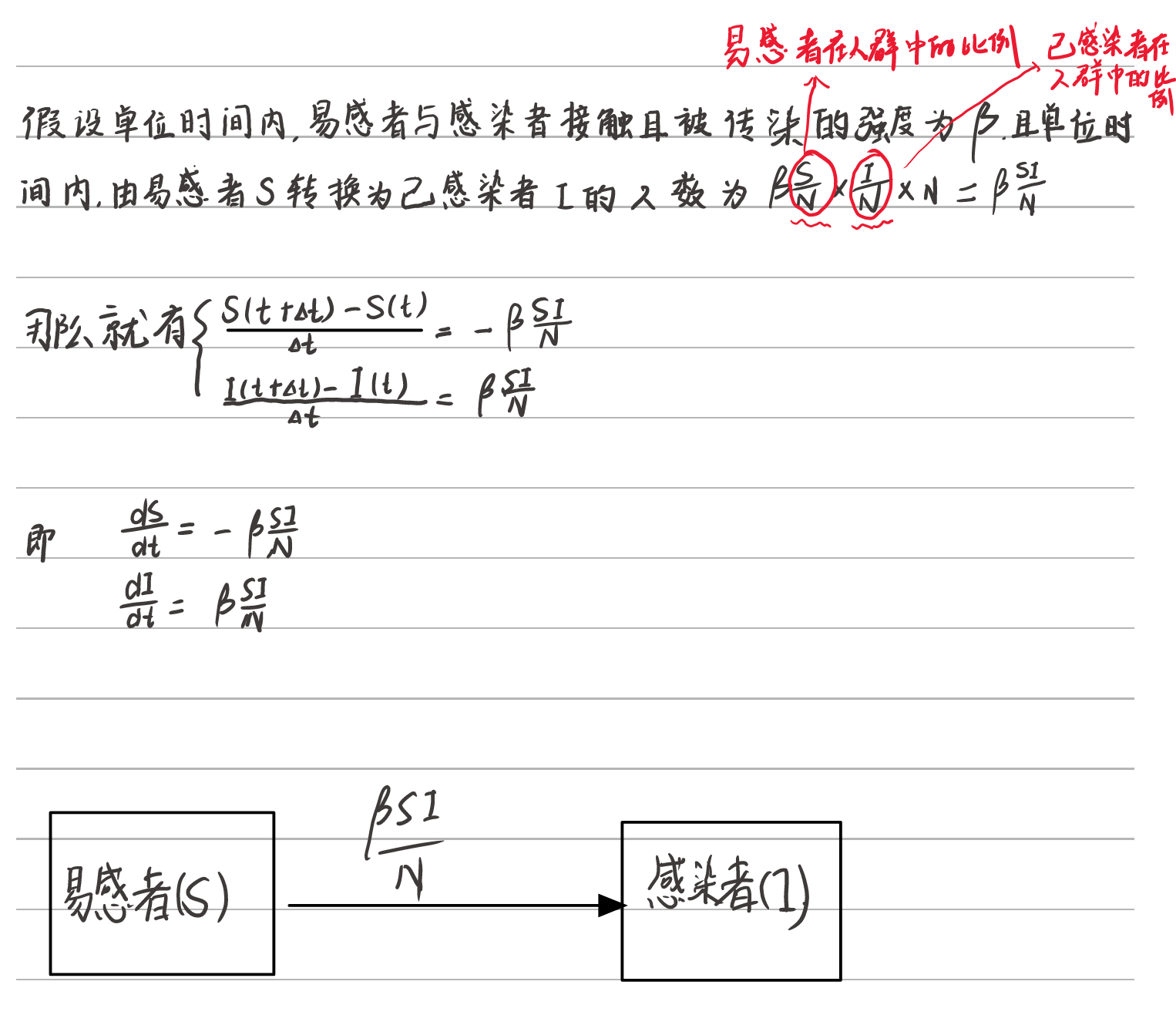
%% 直接求微分方程的解析解
dsolve('Dx1 = -0.1 * x1 * x2 / 1000', 'Dx2 = 0.1 * x1 * x2 / 1000','x1(0) = 999, x2(0) = 1', 't');
%% 根据S + I = N做一个化简
x1 = dsolve('Dx1 = -0.1 * x1 * (1000 - x1) / 1000', 'x1(0) = 999', 't');
x2 = 1000 - x1;
figure(1)
fplot(x1, [0 200], 'b')
hold on
fplot(x2, [0 200], 'r')
legend('易感者', '感染者')
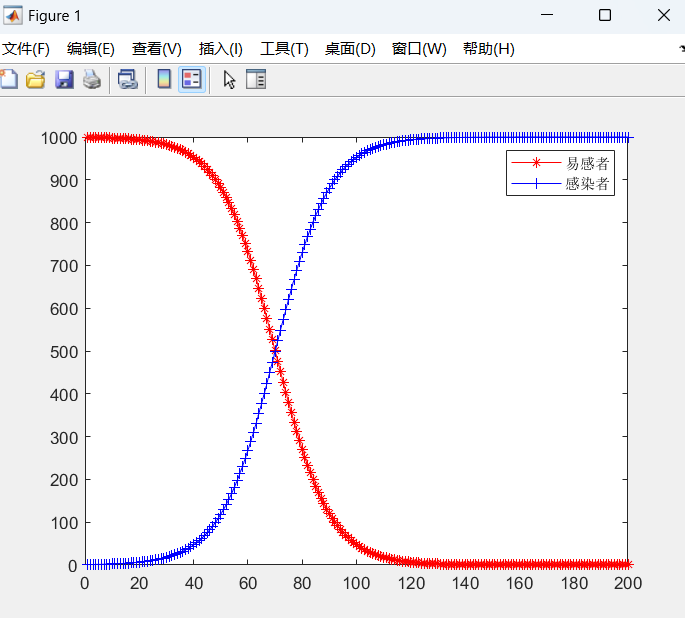
%% 这道题目可以求出解析解,但是后面的大部分题目都是求不出解析解这里我们再熟悉一遍数值解的求解过程
clc; clear
global TOTAL_N
TOTAL_N = 1000;
i0 = 1;
s0 = 999;
[t, x] = ode45('fun1', [1:200], [s0, i0]);
plot(t, x(:, 1), 'r-*');
hold on
plot(t, x(:, 2), 'b-+')'
legend('易感者', '感染者')
function dx = fun1(t, x)
global TOTAL_N
beta = 0.1;
dx = zeros(2, 1);
dx(1) = - beta * x(1) * x(2) / TOTAL_N;
dx(2) = beta * x(1) * x(2) / TOTAL_N;
end
SIS模型(普通传染病模型 )

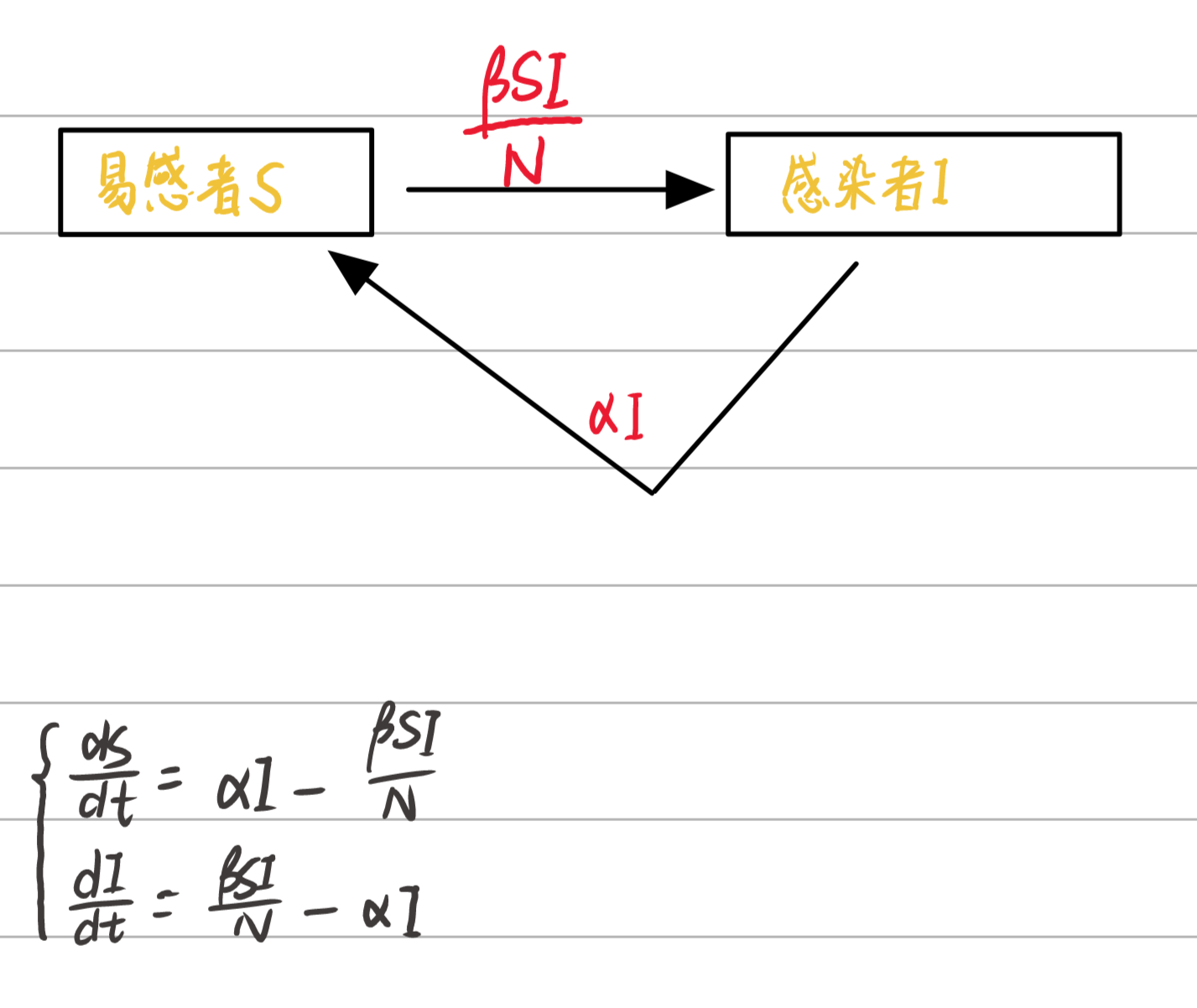
%%
clc;clear
global TOTAL_N
TOTAL_N = 1000;
global alfa;
alfa = 0.06;
global beta
beta = 0.1;
i0 = 1;
s0 = 999;
[t, x] = ode45('fun1', [1:500], [s0, i0]);
plot(t, x(:, 1), 'r-*');
hold on
plot(t, x(:, 2), 'b-+')'
legend('易感者', '感染者')
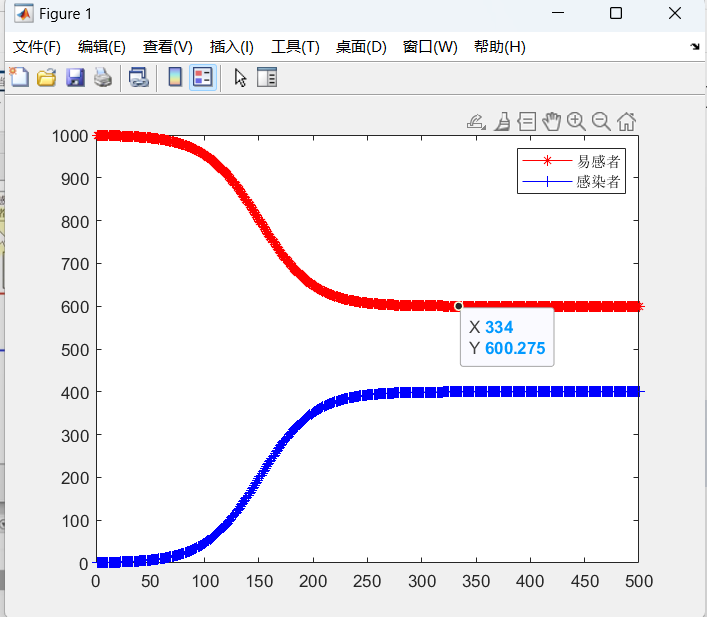
SIR模型

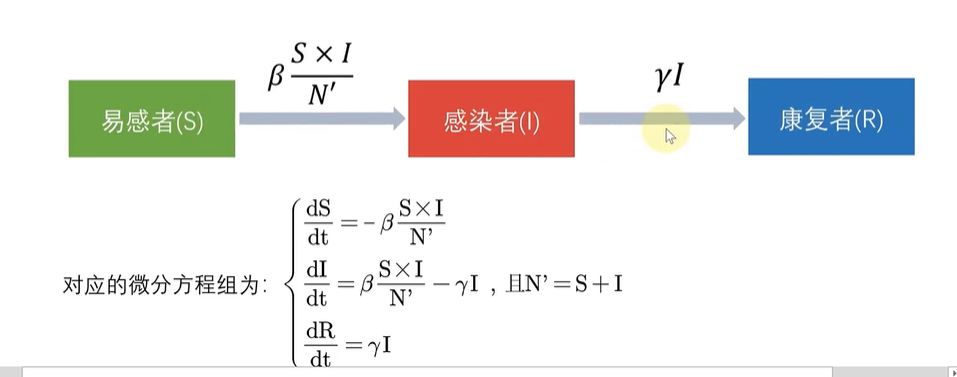
这里关于总人数毫无疑问 N = S + I + R但是在传染过程中,由于康复者已经有抗体且不会再被感染,所以这里有效人群就不能再把R计算在内了,N’ = S + I
%%
clc; clear all;
N = 1000;
i0 = 1;
s0 = 999;
r0 = 0;
[t, x] = ode45('fun1', [1:500], [s0 i0 0]);
x = round(x);
figure(1);
plot(t, x(:, 1), 'r-');
hold on
plot(t, x(:, 2), 'b-');
hold on
plot(t, x(:, 3), 'g-');
hold on
legend('易感者S','感染者I','康复者R')
function dx = fun1(t, x)
beta = 0.1;
gamma = 0.02;
% x(1)表示S,x(2)表示I, x(3)表示R
dx = zeros(3,1);
C = x(1) + x(2);
dx(1) = - beta * x(1) * x(2) / C;
dx(2) = beta * x(1) * x(2) / C - gamma * x(2);
dx(3) = gamma * x(2);
end
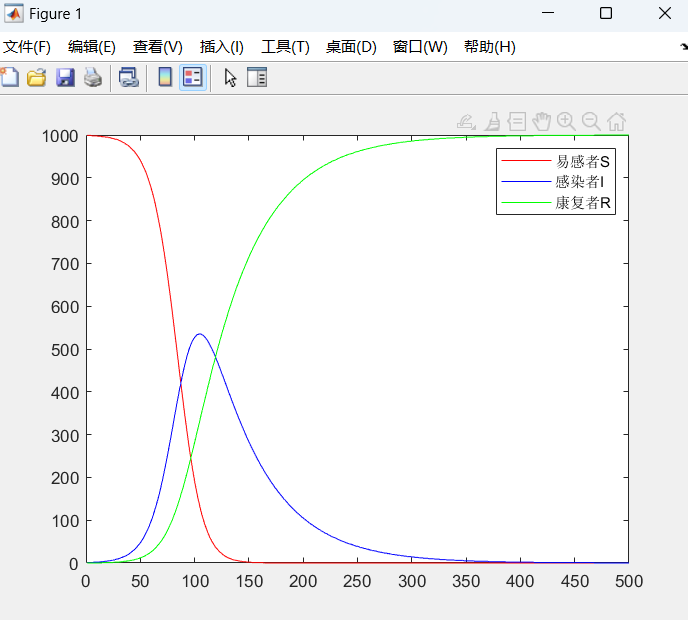
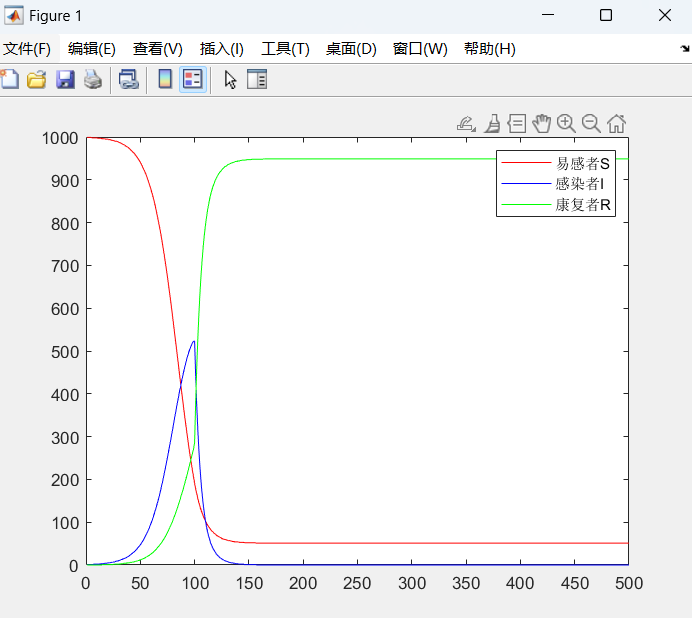
对SIR模型的拓展

function dx = fun1(t, x)
beta = 0.1;
gamma = 0.02;
if t > 100
gamma = gamma * 10;
end
% x(1)表示S,x(2)表示I, x(3)表示R
dx = zeros(3,1);
C = x(1) + x(2);
dx(1) = - beta * x(1) * x(2) / C;
dx(2) = beta * x(1) * x(2) / C - gamma * x(2);
dx(3) = gamma * x(2);
end
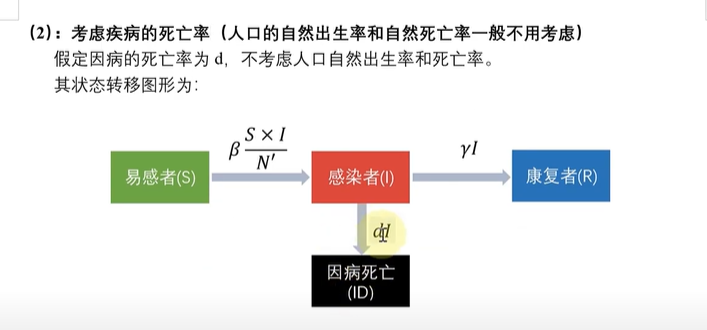
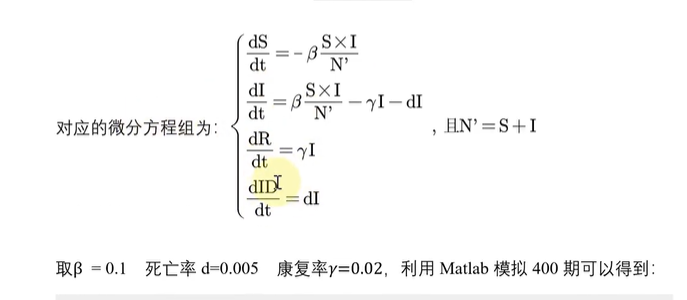
拓展2:考虑死亡率
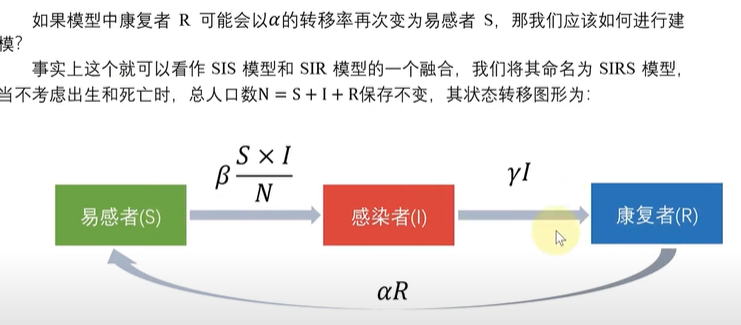
SIRS模型