1.摘要

最近，将低分辨率高光谱图像（LR-HSI）与不同卫星的高分辨率多光谱图像（HR-MSI）融合已成为提高HSI分辨率的有效方法。然而，由于不同的成像卫星、不同的照明条件和相邻的成像时间，LR-HSI和HR-MSI可能不满足现有工作所建立的观测模型，并且它们难以进行配准。为解决上述问题，我们针对来自不同卫星的LR-HSI和HR-MSI建立新的观测模型，然后提出了一个基于深度学习的框架，用于解决多卫星HSI融合的关键步骤，包括图像配准、模糊核学习和图像融合。具体而言，我们首先构建一个名为RegNet的卷积神经网络（CNN），用于生成LR-HSI和HR-MSI之间的像素级偏移，这些偏移用于将LR-HSI进行配准。接下来，根据新的观测模型，我们构建了一个小型网络，称为BKLNet，用于学习光谱和空间模糊核，其中BKLNet和RegNet可以联合训练。在融合部分，我们通过使用学习到的空间模糊核对配准数据进行下采样，进一步训练了一个名为FusNet的网络。大量实验证明了所提出框架在HSI配准和融合准确性方面的优越性。

2.引言

将不同卫星的低分辨率高光谱图像（LR-HSI）和高分辨率多光谱图像（HR-MSI）进行融合是获取载人高分辨率高光谱图像（HR-HSI）的一种有效和便捷的方法，也称为HSI锐化或HSI超分辨率。值得强调的是，由于不同的成像卫星、照明条件和相邻成像时间，融合前的LR-HSI和HR-MSI的预处理步骤变得尤为重要，包括精确的图像配准和合适的观测模型构建。精确的像素级配准是确保融合HR-HSI中的光谱和空间信息的关键。

传统的图像配准方法大致可以分为两类：基于区域的方法和基于特征的方法。

• 基于区域的方法通常使用原始图像强度值来解决图像配准问题，例如相关方法、互信息方法等。这些方法不需要图像中的显著结构特征，但对不同的照明和畸变非常敏感。
• 基于特征的图像配准方法在多光谱图像配准中得到广泛应用，如尺度不变特征变换（SIFT）、加速鲁棒特征（SURF）和深度特征等。然而，不同的地形和巨大的空间分辨率差距使得图像配准困难，并且未准确配准的图像将导致错误的模糊核估计。

本文介绍了一种新颖的基于深度学习的HSI融合框架，用于解决多卫星合作融合问题中的关键步骤，包括图像配准、模糊核学习和图像融合。具体而言，该深度框架包含两个部分，即预处理部分和图像融合部分。在预处理部分，我们对经典观测模型引入了一个额外的线性函数，以弥合来自不同成像卫星的LR-HSI和HR-MSI之间的光谱差距。我们进一步构建一个CNN来生成LR-HSI的像素级偏移量，根据参考HR-MSI，然后将其用于对LR-HSI进行重采样。接下来，根据新的观测模型，构建了一个用于学习空间和光谱模糊核的小型网络。通过解决一些梯度推导问题，我们将配准网络与模糊核学习网络相结合，并将它们一起训练。一旦获得了配准的两幅图像和模糊核，我们将以零样本学习的方式开始HSI融合部分。我们使用学习到的空间模糊核对配准后的两幅图像进行下采样，构建训练对，然后使用快速残差CNN进行HSI融合。此外，我们收集了四个真实的多卫星HSI融合数据集来评估所提出的框架。该研究的贡献主要体现在以下四个方面：

1）我们为不同成像卫星、传感器参数、照明和不同成像时间条件下的LR-HSI和HR-MSI给出了新的观测模型。

2）据我们所知，我们是第一个从LR-HSI和HR-MSI的观测模型入手解决图像配准问题。通过引入可求导的高斯模糊核，我们可以联合优化图像配准和模糊核学习。

3）我们进一步为HSI融合网络引入位置编码洗牌和逆洗牌层，可以在LR-HSI和HR-MSI不完全对齐时保留高分辨率的空间结构。

4）我们收集了四个真实的多卫星HSI融合数据集，并验证了许多深度HSI融合方法可以在所提出的框架基础上扩展到多卫星HSI融合任务。

3.相关工作

在过去几十年中，已经提出了大量的高光谱图像（HSI）融合方法，包括组分替代（CS）方法 [25]，[27]，多分辨率分析（MRA）方法 [28]，[29]，基于优化的方法 [36]，[37]，[38]，[39]，[40]，[41]，[42]，[43]，[44]，以及数据驱动的方法 [30]，[31]，[32]，[34]，[46]，[47]。CS方法使用一组系数生成类似于全色图像的强度图，这组系数应符合两个相机的相对光谱响应函数（SRF），即光谱模糊核。在[25]中，专利提出了一种Gram-Schmidt（GS）光谱Pansharpening方法，它对所有LR-HSI的波段进行平均以计算模拟强度图像。与CS方法不同，MRA方法可以有效避免由于不准确的光谱模糊核引起的融合图像的光谱失真，它们利用全色图像提取空间细节，然后将其添加到LR-HSI中。但另一个问题是，为了获得适当的细节，我们通常使用高斯核对全色图像进行模糊和下采样，这个核应该接近两个相机的相对点扩散函数（PSF），即空间模糊核。在[29]中，作者提出了一种融合框架，该框架使用广义拉普拉斯金字塔（GLP）的减少滤波器，并结合成像相机的调制传递函数（MTF）。

空间和光谱模糊核是基于优化的方法的基石，它们用于构建目标函数。这些方法通常使用一些先验条件来解决优化问题，如高斯先验 [39]，稀疏先验 [36]，[37]，[38]，[40]，[42]，[49]，低秩先验 [41]，[50]，甚至是深度先验 [43]。在[41]中，Charis等人认为HSI融合问题类似于HSI解混合，提出了一种可以将输入的LR-HSI和HR-MSI共同解混合成纯物质反射光谱的方法来实现HSI融合。在[42]中，Dong等人利用HR-HSI的稀疏先验知识来估计系数和光谱基底，采用非负字典学习实现更清晰的HSI融合。此外，Zhang等人在[50]中提出了一种基于低秩Tucker表示的HSI融合模型，带有图正则化，可以保持光谱平滑性和空间一致性。然而，上述优化方法恢复的HR-HSI的质量高度依赖于预定义的先验条件，换句话说，预定义的先验条件往往不足以准确刻画HSI复杂的空间和光谱结构。在[43]中，Dian等人将深度先验引入传统优化框架，他们利用残差CNN来开发所需的HR-HSI图像先验，进而用于联合优化最终的HR-HSI。

随着深度学习在各个领域的一系列成就 [6]，[52]，[53]，[54]，[55]，许多数据驱动的深度学习模型 [30]，[31]，[32]，[34]，[46]，[47]，[51]，[56]已被引入Pansharpening或HSI融合中，这些模型可以通过输入大量的LR-HSI、HR-MSI和参考HR-HSI训练对来学习复杂的映射函数。在[30]中，作者首次提出利用Pansharpening CNN（PNN）进行融合任务，该模型只含有三层但表现出良好性能。在[32]中，Yang等人将领域特定知识融入到PanNet架构中，该模型使用高通滤波后的残差细节图像训练模型的参数。在[33]中，Han等人提出了一个旨在进行深度空间和光谱融合的轻量级HSI融合架构，他们将HR-MSI连续堆叠到特征图中，以实现HR-HSI的清晰空间细节重建。在[46]中，Xie等人构建了一个新颖的MHFNet模型，通过将复杂的优化问题展开为端到端的深度架构，可以考虑LR-HSI和HR-MSI的观测模型。在[47]中，Wang等人引入了一个深度盲融合网络（DBIN），可以迭代地交替优化观测模型和融合过程。当将这些模型应用于实际HSI融合场景时，由于所需的HR-HSI是未知的，观测模型的空间模糊核通常用于对原始LR-HSI和HR-MSI进行模糊和下采样，构造训练对，遵循Wald协议 [57]，其中原始观测的LR-HSI被视为参考HR-HSI标签。这种训练策略被称为零样本学习 [58]，已经在许多方法中提到过 [30]，[31]，[32]，[46]。零样本学习的优势在于它只需要空间模糊核，这可以用于解决多卫星HSI融合中可能不存在准确光谱模糊核的问题。

4.方法

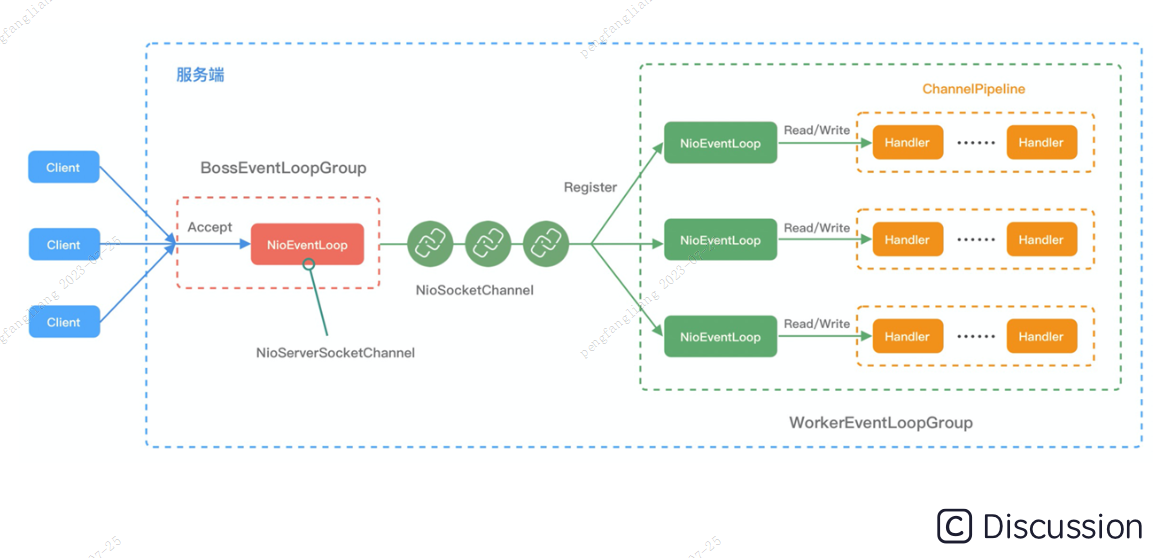
在本文中，我们介绍了用于多卫星HSI融合的新观测模型和深度框架（DFMF），旨在解决融合问题中的关键步骤，包括图像配准、模糊核学习和图像融合。深度框架由两个主要部分组成：a) 预处理部分 b) HSI融合部分。DFMF的结构如图1所示。

4.1 观测模型

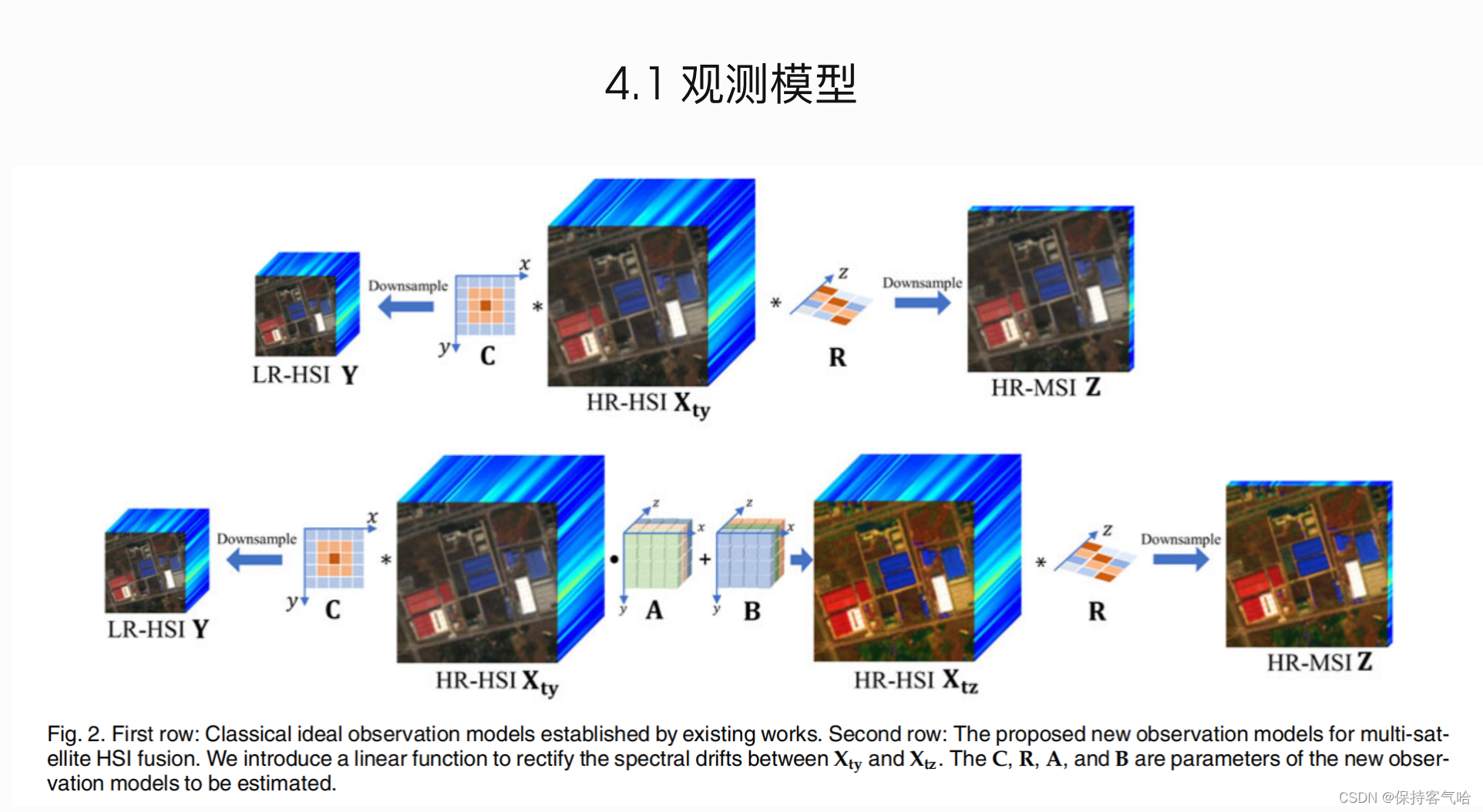
观测模型描述LR-HSI、HR-MSI和目标HR-HSI之间的关系，在HSI融合中至关重要。HSI融合过程是将HR-MSI $Z\in R^{w\times h\times 1}$ (l=1表示全色影像)与相应的LR-HSI $Y\in R^{w\times h\times L}$, (L是光谱波段数)进行融合，得到目标HR-HSI $X_{ty}\in R^{W\times H\times L}$。如图2所示，LR-HSI Y由HR-HSI $X_{ty}$退化得到，这一过程可以表达为：

$$Y=(X_{ty}\ast C{)}_{\downarrow spa}+N_y,(1)$$

其中 * 和 $\downarrow spa$表示空间维度的卷积和下采样操作，下采样比例为s，即HR-HSI的GSD与LR-HSI的GSD之比，s = W/w。C称为两个相机之间的相对点扩散函数（PSF），即空间模糊核，$N_y$代表噪声项。进一步，一个理想的模糊核C可以近似为高斯分布：

$$C(m,n,s)=\frac{1}{\sqrt{2\pi s}}{e}^{-(m^2+n^2)/(2{\sigma }^2))},where(m,n)\in [k,k+1)$$

​ 其中(m, n)表示核中某点的坐标，s是标准差，k表示高斯核的半径。因此，我们只需要估计空间模糊核C的k和s。

类似地，现有的研究假设HR-MSI Z也由相同的HR-HSI $X_{ty}$退化而来。因此，$X_{ty} $和 Z 之间的关系，即观测模型为：

$$Z=(X_{ty}\ast C{)}_{\downarrow spe}+N_z,(3)$$

其中 $\downarrow spe$ 和 * 表示光谱维度的下采样和卷积操作，这个过程也可以描述为光谱维度的张量矩阵乘积。类似地，$N_z$表示Z中的噪声，R是相对光谱响应函数（SRF），即光谱模糊核，其大小为L×l。光谱模糊核R的每列之和为1：

${\Sigma }_{i=1}^L{r}_i^j=1,r_j^i\ge 0,forj=1,2,3,...,l(4)$$

其中$r_i^j $表示R的第j列中第i个元素，因此光谱模糊核中有$L * l$个可训练参数。

然而，在多卫星HSI融合中，不同的卫星影像、光照条件和成像时间会直接导致LR-HSI和HR-MSI之间的光谱差异，即LR-HSI Y和HR-MSI Z来自不同的HR-HSI。因此，我们引入另一个HR-HSI $X_{tz}$，并将其形式化为：

$$Z=(X_{tz}\ast R{)}_{\downarrow spe}+N_z,(5)$$

其中$X_{tz}$是Z对应的HR-HSI。如图2所示，为了弥合$X_{ty}和X_{tz}$之间的光谱漂移差距，我们进一步假设$X_{ty}和X_{tz}$是逐波段线性的关系，可以表示为：

$$X_{tz}=A\odot X_{ty}+B,(6)$$

其中⊙表示逐元素相乘，A和B是线性模型中的两个权重张量，每个波段的元素都相同。可以看出，所有待估计的两个观测模型的参数为C、R、A和B，共有2 + L*l + L + L个参数。

4.2 CNN-Based Registration

与自然场景图像的图像配准任务不同，我们可以通过利用遥感图像的地理坐标（例如有理多项式系数（RPC）正射校正）将来自不同卫星的HR-MSI和LR-HSI统一到一个坐标系统中。然而，这种方式的准确性通常不足，意味着在RPC正射校正后，两个图像之间仍然存在一些像素偏移。对于未精确配准的图像，我们无法找到它们的观测模型，更不用说实现像素级的图像融合。

为了使LR-HSI和HR-MSI严格满足新的观测模型所描述的空间和光谱关系，我们需要首先进行精确的图像配准。在图3中所示，由于训练数据极其有限，即一个LR-HSI和一个HR-MSI，我们构建了一个浅层图像配准网络（RegNet），用于根据参考HR-MSI生成LR-HSI的像素偏移。然后，我们利用这些偏移对LR-HSI进行重采样，使其与输入的HR-MSI对齐。因此，输入LR-HSI的实际覆盖面积应大于输入HR-MSI，为保持两个图像的原始比例，我们在输入HR-MSI的边界处填充了“0”（见图3中HR-MSI的蓝色区域，而虚线内的区域为实际要注册的区域）。

首先，我们对输入的LR-HSI进行通道平均（在图3中的“CA”层），以减少RegNet的参数，并将其与调整大小后的HR-MSI进行串联。然后，我们使用四个卷积（Conv）层，每层使用32个5x5的卷积核和扩张率2，以获得更大的感受野，最后一个Conv层使用2个普通的5x5卷积核来产生偏移。接下来，将两个方向的偏移调整为与输入的LR-HSI相同的大小。同时，我们移除所有卷积核的偏置权重，因为所期望的像素级偏移通常具有广泛的数值范围（从1到数十个像素），但偏置权重使得RegNet的输出更加集中，这对训练过程非常不利。

获得像素级偏移后，我们使用它们将输入的LR-HSI与HR-MSI对齐。由于缺乏目标配准的LR-HSI，我们无法直接训练RegNet。

4.3 Blur Kernel Learning

在图像处理中，准确的模糊核估计也非常重要。在本节中，我们利用新的观测模型来学习模糊核并训练整个预处理部分。具体来说，我们使用频谱核 R 和空间核 C 对 LR-HSI Y 和 HR-MSI Z 进行模糊和下采样，降质的 LR-HSI $Y^{\prime }$ 和 HR-MSI $Z’ $可以表示为：

$$Y^{\prime }=(Y\ast R{)}_{\downarrow spe}(9)$$

$$Z^{\prime }=(Z\ast C{)}_{\downarrow spe}(10)$$

为方便起见，我们省略了观测模型（1）、（5）中的噪声项，并将它们代入式（9）和式（10）中，可以表示为：

$$Y^{\prime }=((X_{ty}\ast C{)}_{\downarrow spa}\ast R{)}_{\downarrow spe}(11)$$

$$Z^{\prime }=((X_{ty}\ast R{)}_{\downarrow spe}\ast C{)}_{\downarrow spa}(12)$$

此外，我们预定义了$ X_{tz} 和 X_{ty} $之间的关系，如 $X_{tz}=A\ast X_{ty}+B$，将其代入式（12）中，可以得到：

$$Z^{\prime }=((A\ast X_{ty}+B)\ast R{)}_{\downarrow spe}\ast C{)}_{\downarrow spa}(13)$$
如果我们使用 A 和 B 将式（1）中的 $X_{ty}$ 映射，并将其代入式（9）中，可以得到：

$$Y^{\prime \prime }=((A\ast X_{ty}+B)\ast C{)}_{\downarrow spa}\ast R{)}_{\downarrow spe}(14)$$
因为空间和光谱降解是两个独立的过程，我们可以发现 $Y^{\prime \prime }$。进一步考虑到 C 和 R 都已归一化，我们将式（14）转换为：

根据公式（10），可以得到：

$$(A\ast Y+B)\ast R\downarrow spe=(Z\ast C)\downarrow spa(16)$$

公式（16）中的关系非常重要，基于此，我们可以建立一个微小的模糊核学习网络。同时，它还使我们可以仅使用 LR-HSI Y 和 HR-MSI Z 训练整个预处理部分。

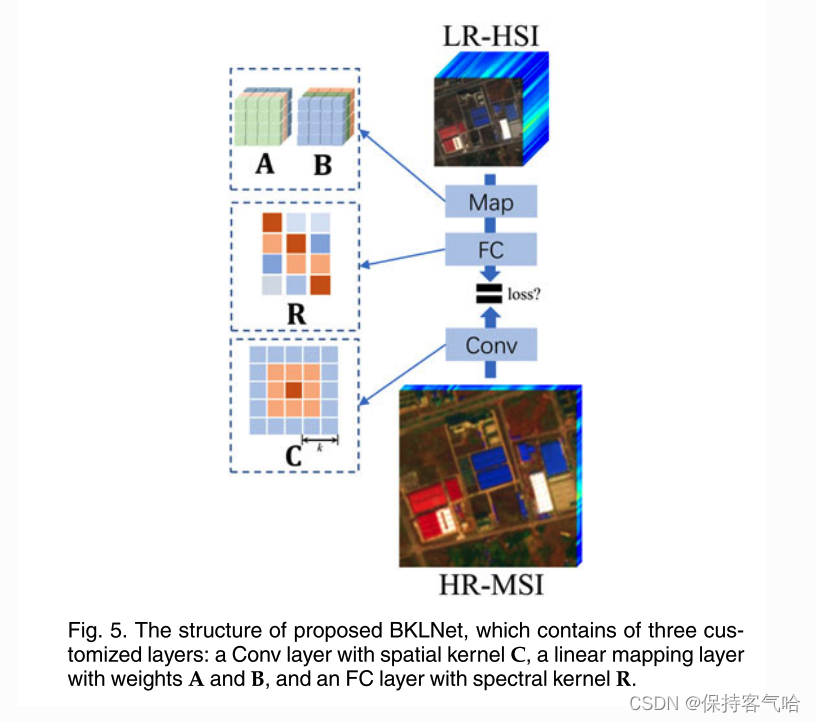
可以很容易地观察到，普通 CNN 中的深度卷积层带有高斯核 C 和步长 s 可以完美地模拟空间模糊和下采样过程。类似地，光谱模糊和下采样过程也可以由具有权重 R 的全连接（FC）层或大小为 l1 * 1 的卷积层模拟。如图 5 所示，

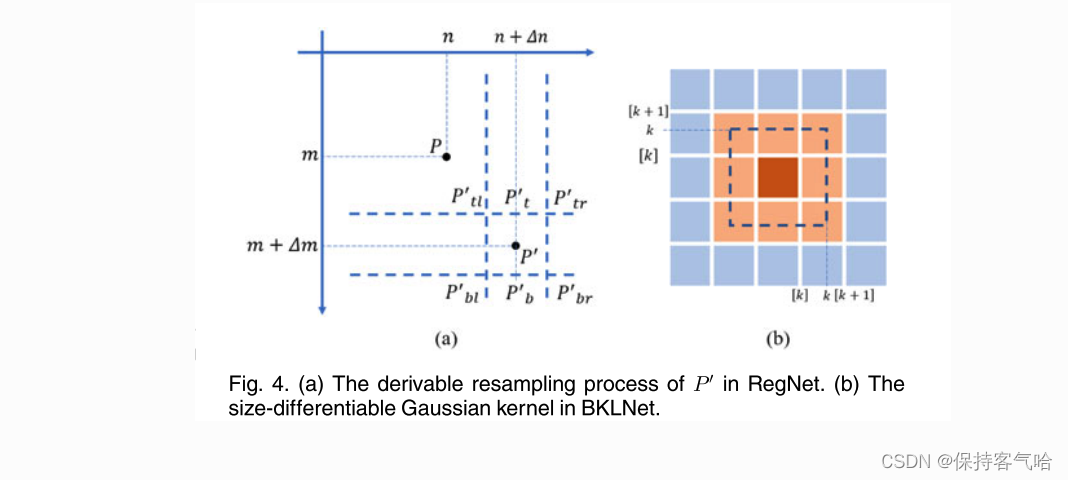
我们引入了模糊核学习网络（BKLNet），它由三个定制的可学习部分组成，一个具有权重 A 和 B 的线性映射层，一个具有光谱核 R 的 FC 层和一个具有空间核 C 的卷积层（见图 5 中的 “Map”、“FC” 和 “Conv” 层）。我们进一步利用线性插值操作使非整数大小的模糊核大小 k 可微分和可训练，表示为：
$$C_k=f(k)C_{[k+1]}+(1-f(k))\ast C_{[k]}(17)$$

其中，$C_k$ 表示大小为 $(2k+1)\times (2k+1)$ 的高斯核，如图 4b 所示

4.4 Joint Training

如上所述，由于不同的成像卫星、不同的光谱响应特性，甚至不同的照明条件，使得公式（16）中的等式关系很难严格正确。因此，我们使用结构相似性指数（SSIM）损失来训练 BKLNet，而不是像素均方误差（MSE）损失，它表示为：

$$loss1=(1-SSIM(Y^{\prime \prime },Z’))+\lambda （k+\sigma )(18)$$

其中，$\lambda$ 表示正则化参数，这里设置为 0.0005。我们限制模糊核大小 k 和标准差 s，以避免在后续的零样本融合部分中由于过度平滑的空间模糊核而导致严重的结构畸变。

此外，由于对 LR-HSI 进行重采样和学习模糊核大小 k 的梯度推导问题已经得到很好地解决，因此我们可以将 RegNet 与 BKLNet 结合起来，然后进行端到端的训练。全局损失函数为：

$$loss2=(1-SSIM(Y^{\prime \prime },Z’))+aTV(off)+\lambda （k+\sigma )(19)$$

其中，TV(off) 表示我们使用 $l_1-TV$ 对预测的偏移进行约束，这可以确保对齐的 LR-HSI 的平滑性，a 设置为 0.01。我们使用 Adam 优化器对整个预处理部分进行 20 轮训练，学习率设置为 0.005。

4.5 Multi-Satellite HSI Fusion

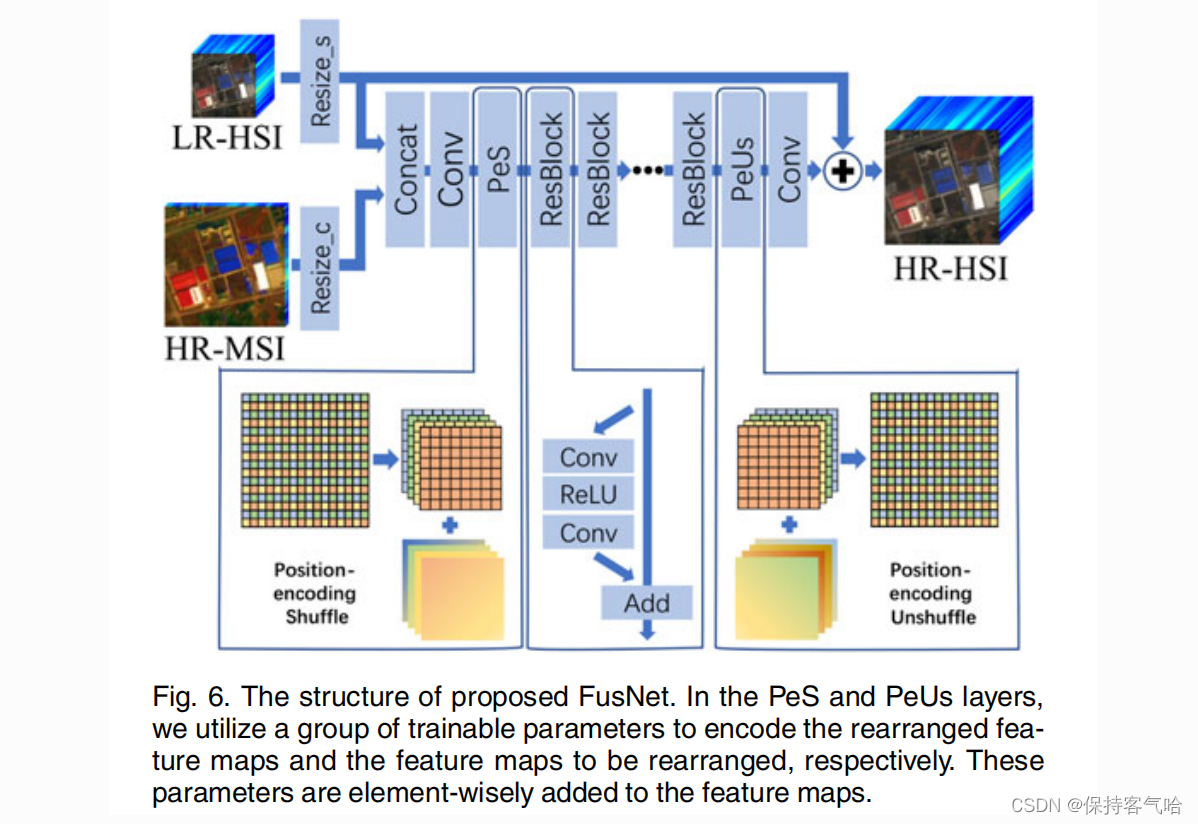
经过预处理步骤，我们可以获得对齐的 LR-HSI、HR-MSI、空间和光谱模糊核。我们采用零样本训练策略进行多卫星 HSI 融合。首先，为了生成训练数据，我们利用学习得到的空间模糊核对对齐的 LR-HSI 和 HR-MSI 进行模糊和下采样（采样比例为 s），并将它们裁剪为图像块。然后，将裁剪后的 LR-HSI 和 HR-MSI 块送入快速 HSI 融合网络（FusNet）进行训练，FusNet 的结构如图 6 所示。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-vGMEF5kk-1690527740730)(/Users/zhangkai/Library/Application Support/typora-user-images/image-20230728150123784.png)]

我们首先将输入的 LR-HSI 块上采样到与 HR-MSI 块在空间维度上相同的大小，并将输入的 HR-MSI 块上采样到与 LR-HSI 块在光谱维度上相同的波段。然后，我们将它们连接起来，并使用一个具有 80 个 1 * 1 卷积核的普通卷积层进行通道压缩。如图 6 所示，为了提高模型的训练效率，我们引入了 ”Position-encoding Shuffle” 和 ”Position-encoding Unshuffle” 层。与常用的 ”Shuffle” 和 ”Unshuffle” 层不同，我们在这些层中引入了受最新的 transformer[62]启发的位置编码操作，它可以在重新排列像素时保留 HR-MSI 的高分辨率空间结构。具体来说，我们引入了一组可训练参数到这些层中，然后将这些参数逐元素加到特征图上。接下来，我们使用五个 ResBlocks 进行更深的特征提取，每个 ResBlocks 中的卷积层具有 320 个 3 * 3 的卷积核。最后，我们使用具有 L 个 3 * 3 卷积核的卷积层进行通道扩展，并将它们添加到重新调整大小的输入 LR-HSI 中，以重构所需的 HR-HSI。使用平均绝对误差（MAE）损失进行 FusNet 的训练，我们还使用 Adam 优化器[60]，学习率设置为 0.0001，并在每 20 轮训练后降低十倍。