前面的内容:
一. 器件选型心得(系统设计)--1_goldqiu的博客-CSDN博客
一. 器件选型心得(系统设计)--2_goldqiu的博客-CSDN博客
二. 多传感器时间同步方案(时序闭环)--1
三. 多传感器标定方案(空间同步)--1
在进行多传感器融合算法部署之前,除了要进行多传感器时间同步,也就是时序闭环;还需要进行多传感器标定,也就是空间同步。
我们要做的就是:将所有传感器的成像结果统一到同一坐标系下。
多传感器标定的参数包括内参和外参,其核心问题是求解非线性最小二乘问题,对应非线性优化方法。
非线性优化
最简单的方法是梯度下降,即找一个初始值,沿着负梯度(非线性函数对求解参数进行求导)的方向逐步迭代,当迭代步长足够小时,即完成求解。
我们定义成数学问题,对于:

我们的思路:

非线性优化问题的关键是如何确定∆x。
方法如下:

方法1(最速下降法):步长𝜆不容易确定,容易陷入局部最优,根本原因是仅保留一阶项来近似求解。
方法2(牛顿法):求解Hessian矩阵的计算量比较大,且不容易求解。
方法3(高斯牛顿法):不是对lost-function进行泰勒展开,而是对非线性函数进行一阶泰勒展开,进行一阶线性化近似,然后构建目标函数,目标函数对∆x进行求导,最后求解线性方程组,用Jacobian来近似Hessian。这样的好处是收敛速度较快,特别适用于参数估计问题。然而,由于它基于二次函数的线性化,当目标函数存在较大的非线性特征时,可能会导致迭代过程中发散。
于是便引出LM法:
Levenberg-Marquardt方法:它是一种常用的非线性最小二乘优化算法,结合了最速下降法和高斯牛顿法的优点。它在高斯牛顿法的基础上引入了一个调整因子,以解决高斯牛顿法在目标函数具有较大非线性特征时可能出现的发散问题。
Levenberg-Marquardt法是在Gaussian-Newton法的基础上添加了阻尼因子λ,即求解线性方程:
当λ较大时,相当于梯度下降法,而λ较小时,相当于G-N法。 当问题性质较好时,用高斯牛顿法,若问题接近病态,用LM法,稳定性更好,更容易收敛。
标定问题中的非线性优化
一般我们需要求解变换矩阵T,而R是满足一定约束的。那么,带约束的非线性优化问题,如何求解?
• 用李代数表达位姿,利用李代数求导方法,可转化为无约束优化问题(矩阵群没有加法,只有乘法,不方便求导)
• 沿用非线性优化求解
内参标定
多传感器内参:
| 传感器 | 内参产生原因 | 如何标定 |
|---|---|---|
| 相机 | • 棱镜安装偏移 • 焦距 • 相机坐标系与图像坐标系之间转换关系 | • 可通过算法补偿 • 因工艺问题,需要重标 |
| 激光雷达 | • 激光头的安装位置和角度 • 强度值一致性要求 | • 需要专业设备 • 出厂已标好 |
| 毫米波雷达 | • 发射天线安装位置 • 接收天线距离 | • 需要专业设备 • 出厂已标好 |
| 超声波雷达 | • 压电陶瓷输入的电流电压值 • 安装高度及感知区域扇面尺寸 | • 需要专业设备 • 出厂已标好 |
所以一般我们只需要标定相机内参,即标定相机坐标系到uv坐标系的投影关系。
Camera成像过程的建模
成像两阶段(没有考虑畸变):
-
相机坐标系到图像坐标系
-
图像坐标系到像素坐标系
得到:
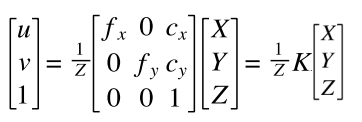
Z被提取出来,表明成像过程失去了深度信息。 fx, fy 为坐标系缩放系数,包含了f焦距信息;Cx, Cy 为坐标系平移量。
Camera成像过程中存在畸变,如何建模?
-
径向畸变:透镜自身形状难以做到完全规则,因此会对光线传播产生影响,从而引起径向畸变
-
切向畸变:机械组件的安装过程中,透镜和成像平面不可能完全平行。
总结整个相机成像过程建模:
(1)自车坐标系到相机坐标系
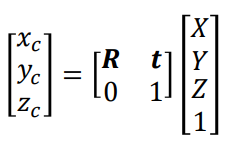
(2)相机坐标系到图像坐标系(不考虑畸变)
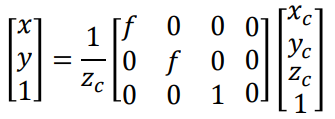
(3)图像坐标系(含去畸变): 将(Xc, Yc, Zc)投影到归一化平面上 ,再进行(径向与切向)畸变修正,得到去畸变后的归一化坐标。
(4)图像坐标系到像素坐标系
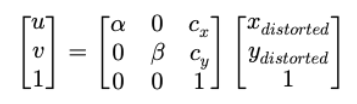
将纠正后的点投影到像素平面,其中 为坐标系缩放系数,Cx, Cy 为坐标系平移量。
通常意义上,相机需要标定的参数如下:
[f, , Cx, Cy, k1, k2, k3, p1, p2]
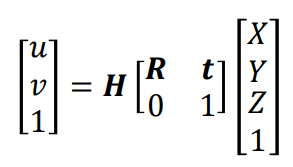
矩阵H内包含f, , Cx, Cy 内参 和 k1, k2, k3, p1, p2 畸变参数。对于每个相机来说,参数都不一致,因此需要标定。
将Camera内参标定问题转化为非线性优化问题
采用棋盘格进行标定(张正友标定法),传统计算机视觉对于棋盘格的角点检测精度高。而棋盘格尺寸是定制的,角点之间的3D位置可计算。
我们需要获得一一对应的多组3D空间点和像素点。而一张棋盘格成像可以建立多组对应关系。

对第k张图片,以棋盘格的原点为基准可定位每一个角点,并满足投影关系如下,找到足够多的对应点:
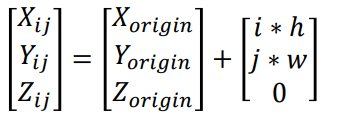
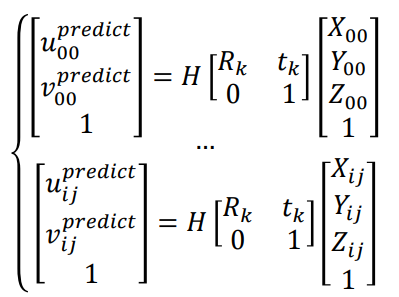
由此构建优化问题:
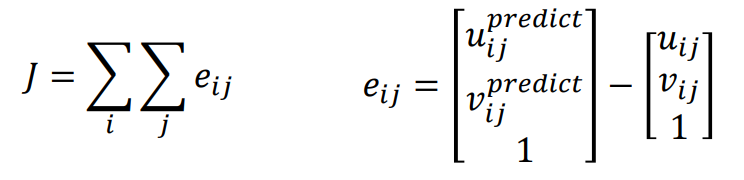
用高斯牛顿法或LM(Levenberg-Marquardt )算法计算出如下参数:
[f, , Cx, Cy, k1, k2, k3, p1, p2]还有R,t,注意这里还得到了相机到自车坐标系的变换。
总结:
假设在相机内参和外参完全已知和正确的情况下,标定板在三维空间中的角点投影到相机像素平面上应该是要和相机像素平面成像的那个角点重合的。但事实上相机的内参和外参是不正确的,所以是不重合的,error不为0,所以我们就是要构建多个三维空间的角点投影到相机像素平面的UV点与原来像素平面的UV点的误差方程,我们的目标是将error逼近0,达到最小,求解出此时的内参和外参。那为什么相机到自车坐标系这个外参也能求得呢,是因为我们已知了棋盘格内部角点的投影关系,这个作为已知量,而外参作为求解量和内参也能够在构建的超定方程中求解出来。
标定实现
二. 多传感器时间同步方案(时序闭环)--1
参考:深蓝学院《多传感器融合感知》