实验十二 图+查找
一、实验目的与要求
1)掌握拓扑排序的应用;
2)掌握查找的概念和算法;
3)掌握查找的基本原理以及各种算法的实现;
4)掌握查找的应用。
二、实验内容
1. 用邻接表建立一个有向图的存储结构。利用拓扑排序算法输出该图的拓扑排序序列。
2. 0~n-1中缺失的数字
一个长度为n-1的递增排序数组中的所有数字都是唯一的,并且每个数字都在范围0~n-1之内。在范围0~n-1内的n个数字中有且只有一个数字不在该数组中,请使用折半查找算法找出这个数字。
示例 1:
输入: [0,1,3]
输出: 2
示例 2:
输入: [0,1,2,3,4,5,6,7,9]
输出: 8
三、实验结果
1)请将调试通过的主要源代码、输出结果粘贴在下面(必要的注释、Times New Roman 5号,行间距1.5倍)
2)简述算法步骤(选画技术路线图),格式如下:
S1:
S2:
3)请分析算法的时间复杂度。
4)请将源代码(必要的注释)cpp文件压缩上传
题目1:
(1.1)实验源代码
#include <iostream>
using namespace std;
//拓扑排序
#define MVNum 100
typedef char VerTexType;
//图的邻接表存储表示
typedef struct ArcNode{
int adjvex;
struct ArcNode *nextarc;
}ArcNode;
typedef struct VNode{
VerTexType data;
ArcNode *firstarc;//指向第一条依附该顶点的边的指针
}VNode, AdjList[MVNum];
typedef struct{
AdjList vertices;//邻接表
AdjList converse_vertices;//逆邻接表
int vexnum, arcnum;//图的当前顶点数和边数
}ALGraph;
//定义顺序栈
typedef struct{
int *base;
int *top;
int stacksize;
}spStack;
int indegree[MVNum];//存放个顶点的入度
spStack S;
//初始化栈
void InitStack(spStack &S){
S.base = new int[MVNum];
if(!S.base)
exit(1);
S.top = S.base;
S.stacksize = MVNum;
}
//进栈
void Push(spStack &S , int i){
if(S.top - S.base == S.stacksize){
return;
}
*S.top++ = i;
}
//出栈
void Pop(spStack &S , int &i){
if(S.top == S.base){
return;
}
i = *--S.top;
}
//判断空栈
bool StackEmpty(spStack S){
if(S.top == S.base){
return true;
}
return false;
}
//确定点v在G中的位置
int LocateVex(ALGraph G , VerTexType v){
for(int i = 0; i < G.vexnum; ++i){
if(G.vertices[i].data == v){
return i;
}
}
return -1;
}
//创建有向图G的邻接表、逆邻接表
int CreateUDG(ALGraph &G){
int i , k;
cout <<"请输入总顶点数,总边数:";
cin >> G.vexnum >> G.arcnum;
cout << endl;
cout << "输入点的名称:" << endl;
for(i = 0; i < G.vexnum; ++i){
cout << "请输入第" << (i+1) << "个点的名称:";
cin >> G.vertices[i].data;
G.converse_vertices[i].data = G.vertices[i].data;
G.vertices[i].firstarc=NULL;//初始化表头结点的指针域为NULL
G.converse_vertices[i].firstarc=NULL;
}
cout << endl;
cout << "输入边依附的顶点:" << endl;
for(k = 0; k < G.arcnum;++k){
VerTexType v1 , v2;
int i , j;
cout << "请输入第" << (k + 1) << "条边依附的顶点:";
cin >> v1 >> v2;
i = LocateVex(G, v1);
j = LocateVex(G, v2);//确定v1和v2在G中位置,即顶点在G.vertices中的序号
ArcNode *p1=new ArcNode;//生成一个新的边结点*p1
p1->adjvex=j;//邻接点序号为j
p1->nextarc = G.vertices[i].firstarc;
G.vertices[i].firstarc=p1;//将新结点*p1插入顶点vi的边表头部
ArcNode *p2=new ArcNode;
p2->adjvex=i;
p2->nextarc = G.converse_vertices[j].firstarc;
G.converse_vertices[j].firstarc=p2;
}
return 1;
}
//求入度
void FindInDegree(ALGraph G){
int i , count;
for(i = 0 ; i < G.vexnum ; i++){
count = 0;
ArcNode *p = G.converse_vertices[i].firstarc;
if(p){
while(p){
p = p->nextarc;
count++;
}
}
indegree[i] = count;
}
}
//有向图G采用邻接表存储结构,若G无回路,则生成G的一个拓扑序列topo[]并,否则ERROR
int TopologicalSort(ALGraph G , int topo[]){
int i , m;
FindInDegree(G);
InitStack(S);
for(i = 0; i < G.vexnum; ++i){
if(!indegree[i]){
Push(S, i); //入度为0者进栈
}
}
m = 0;//对输出顶点计数,初始为0
while(!StackEmpty(S)){
Pop(S, i);//将栈顶顶点vi出栈
topo[m]=i;//将vi保存在拓扑序列数组topo中
++m;//对输出顶点计数
ArcNode *p = G.vertices[i].firstarc;//p指向vi的第一个邻接点
while(p){
int k = p->adjvex;//vk为vi的邻接点
--indegree[k];//vi的每个邻接点的入度减1
if(indegree[k] ==0){
Push(S, k); //若入度减为0,则入栈
}
p = p->nextarc;//p指向顶点vi下一个邻接结点
}
}
if(m < G.vexnum){
return 0;
}
return 1;
}
int main(){
ALGraph G;
CreateUDG(G);
int *topo = new int [G.vexnum];
cout << endl;
cout << "有向图的邻接表、逆邻接表创建完成" << endl<< endl;
if(TopologicalSort(G , topo)){
cout << "该有向图的拓扑有序序列为:";
for(int j = 0 ; j < G.vexnum; j++){
if(j != G.vexnum - 1){
cout << G.vertices[topo[j]].data << " , ";
}
else{
cout << G.vertices[topo[j]].data << endl << endl;
}
}
}
else{
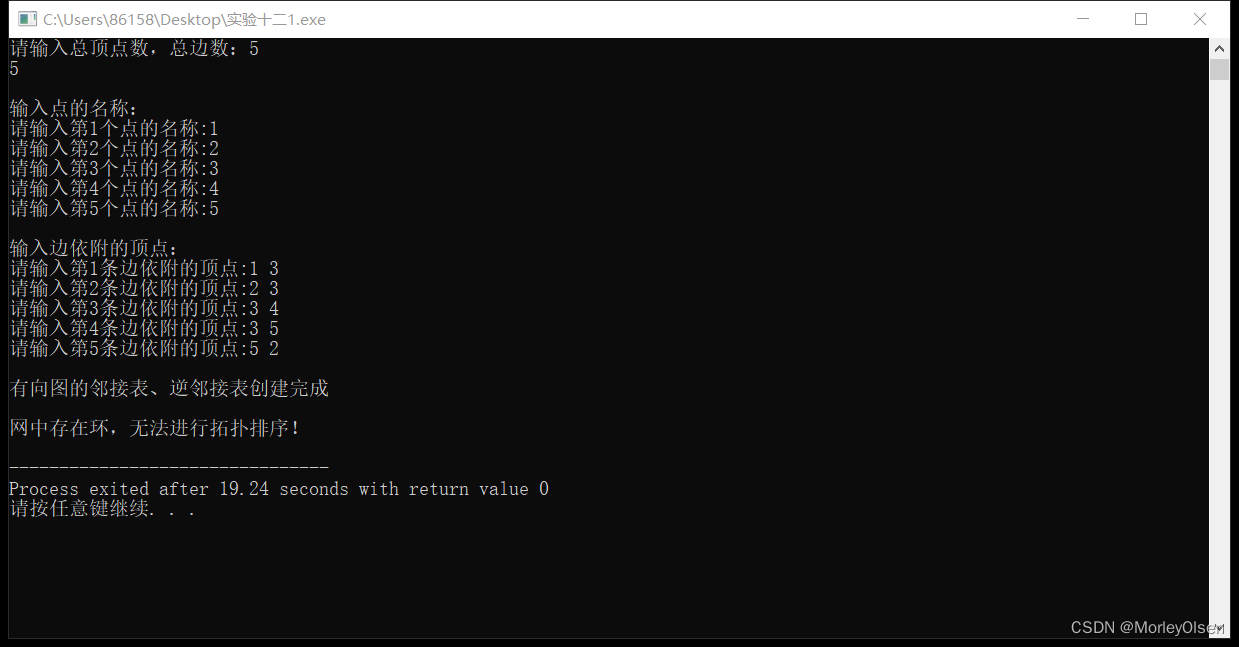
cout << "网中存在环,无法进行拓扑排序!" <<endl;
}
return 0;
}
(1.2)测试用例及其输出结果
测试用例1

程序运行结果1:

测试用例2:
程序运行结果2:
(2)简述算法步骤
S1:构建邻接表结构。

S2:构建栈,并定义初始化栈、进栈、出栈、判断空栈这四个函数体。初始化栈时,创建一个新的数组存放数据,并令顶指针为初始位置,栈空间大小为最大数。进栈时,先判断是否栈满,如果栈已满则直接return,如果栈未满则顶指针存入数据后后置++。出栈时,先判断是否栈空,如果栈空则直接return,如果栈非空则顶指针下移一位后弹出存放的数据。判断空栈时,如果顶指针和底指针相等,则当前栈为空栈,否则当前栈非空。

S3:构建“确定节点v在邻接表中的位置”函数。主要通过for循环遍历G,如果当前节点数据与目标节点v匹配,则返回当前节点的位置。如果循环结束后依然未匹配,则返回-1数值,表示节点v不存在于有向图G中。

S4:构建“创建有向图G的邻接表和逆邻接表”函数。首先需要输入总顶点数和总边数、各节点的名称、各边依附的节点信息。通过输入各节点的名称时生成邻接表和逆邻接表,并将指向第一条依附该节点的边的指针置空。接着通过输入各边依附的节点信息时,确定两个节点在有向图G中的位置,并生成两个个临时新边界点p1和p2,令p1、p2的邻接点序号分别为该边第二个节点的位置和第一个节点的位置,然后令p1、p2的下一条边为另外一个节点的第一条边指针。

S4:构建“求入度”函数。通过遍历节点,设置临时边指针p为逆邻接表中当前遍历节点的第一条边,当p非空的时候,p指向其下一条边,计数变量加一,然后输出当前节点的入度数。

S5:构建“邻接表存储结构”函数。先求出有向图G中各节点的入度,然后初始化一个栈,通过for循环遍历有向图G,并将入度为0的节点进行进栈操作。当存入的栈非空时,将顶指针指向的节点进行出栈操作,并保存在拓扑序列数组中,计数输出节点个数。接着,再临时新建一个p指针表示当前节点的第一条边指针。当p非空时,vk是vi的邻接点,vi的每个邻接点入度减去1。如果vk的入度为0,则将vk入栈,并令p指向vi的下一个邻接节点。最后通过if条件语句判断是否有回路,如果有回路则返回0,否则返回1。

S6:构造主函数。主要通过调用上述函数,得出拓扑序列。

(3)分析算法的时间复杂度
拓扑排序算法的主要思想为:
第一步,栈S初始化,累加器count初始化。
第二步,扫描顶点表,将没有前驱(即入度为0)的顶点压栈。
第三步,当栈S非空时循环,(1)vj=退出栈顶元素;输出vj;累加器加1;(2)将顶点vj的各个邻接点的入度减1;(3)将新的入度为0的顶点入栈。
第四步,if (count<vertexNum) 输出有回路信息。
如果AOV网络有n个顶点,e条边,在拓扑排序的过程中,搜索入度为零的顶点所需的时间是O(n)。在正常情况下,每个顶点进一次栈,出一次栈,所需时间O(n)。每个顶点入度减1的运算共执行了e次。所以总的时间复杂为O(n+e)。
题目2:
(1.1)实验源代码
#include <cstdio>
#include <iostream>
using namespace std;
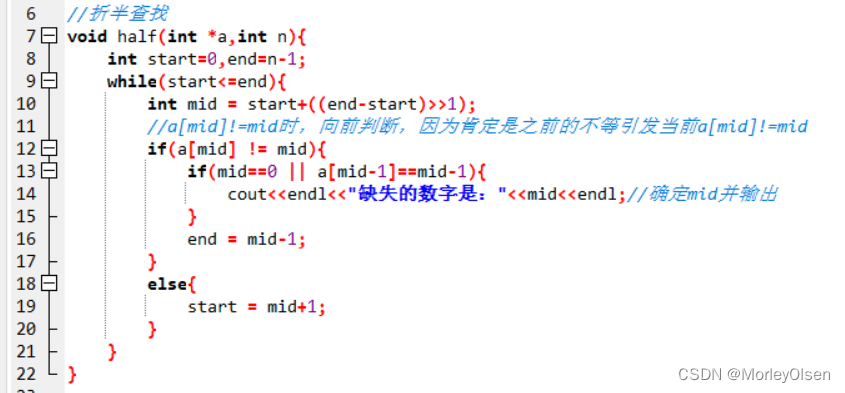
void half(int *a,int n){
int start=0,end=n-1;
while(start<=end){
int mid = start+((end-start)>>1); //折半查找
//a[mid]!=mid时,向前判断,因为肯定是之前的不等引发当前a[mid]!=mid
if(a[mid] != mid){
if(mid==0 || a[mid-1]==mid-1){
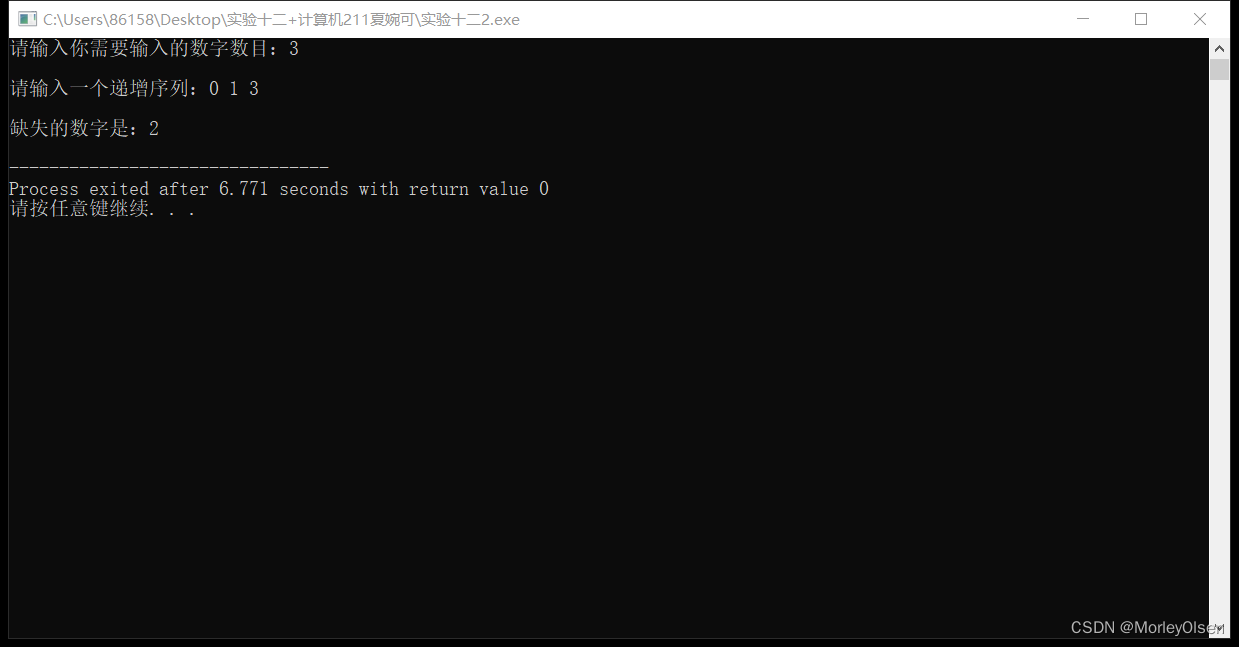
cout<<endl<<"缺失的数字是:"<<mid<<endl;//确定mid并输出
}
end = mid-1;
}
else{
start = mid+1;
}
}
}
int main(){
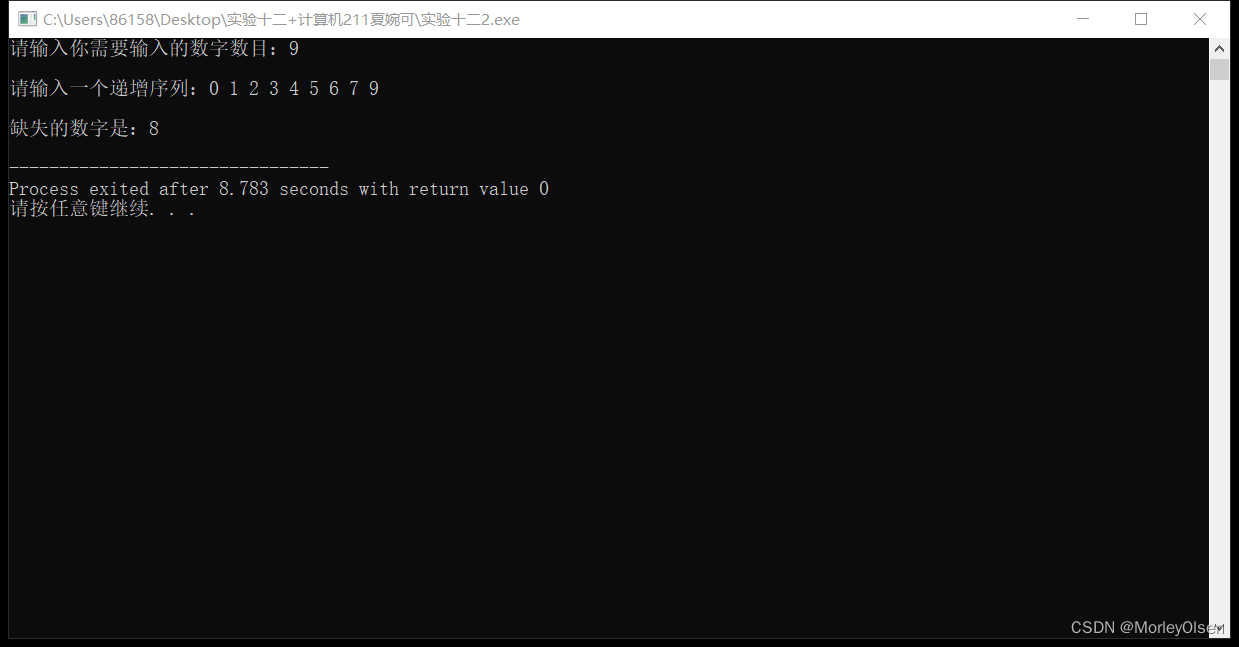
int n,i,a[10000];
cout<<"请输入你需要输入的数字数目:";
cin>>n;
cout<<endl<<"请输入一个递增序列:";
for(i=0;i<n;i++){
cin>>a[i];
}
half(a,n);
return 0;
}
(1.2)测试用例及其输出结果
测试用例1:
n=3
array=【0,1,3】
程序运行结果1:
测试用例2:
n=9
array=【0,1,2,3,4,5,6,7,9】
程序运行结果2:
(2)简述算法步骤
S1:构造“折半查找”函数。首先设置下标值start、end和mid,mid即为缺失的数字的下标,之后利用while循环进行查找循环。每次折半查找都要更新min的值,由于该序列是隔1递增的,因此查找的终止条件为a[mid]!=mid。
S2:构造主函数。输入需要查找的数字和已知的递增序列,再通过调用half函数输出运行结果。

(3)分析算法的时间复杂度
折半查找判定树的构造:如果当前low和high之前有奇数个元素,则mid分隔后,左右两部分元素个数相等。如果当前low和high之间有偶数个元素,则mid分隔后,左半部分比右半部分少一个元素。
在折半查找的判定树中,若mid=(low+high)/2,向下取整,则对于任何一个结点,因此必有:右子树结点-左子树结点数=0或1。当有奇数个元素时等于0,有偶数个元素时等于1。所以折半查找判定数一定是平衡二叉树,树的深度为[log2n]+1。查找成功时所进行的关键码比较次数至多为[log2n]+1,查找不成功时和给定值进行比较的次数最多不超过树的深度。
综上所述,折半查找的时间复杂度为O(log2n)。
【补充:】请使用顺序查找算法进行时间复杂度对比分析。
【选作:】使用索引顺序表查找算法进行时间复杂度、空间复杂度的对比分析。
三、实验结果
顺序查找算法:
(1)源代码
//顺序查找算法
#include <cstdio>
#include <iostream>
using namespace std;
int main(){
int n,a[1000],i;
cout<<"请输入n:";
cin>>n;
cout<<"请输入排序好的数组:";
for(i=0;i<n;i++){
scanf("%d",&a[i]);
}
int j=0,loss=0,flag=0;
while(j<n){
if(a[j]!=j){
loss=j;
flag++;
break;
}
j++;
}
if(!flag){
loss=n;
}
cout<<"缺失值为:"<<loss;
return 0;
}(2)测试用例及其运行结果



(3)时间复杂度分析
最好情况:一次比较就找到所要查找的元素,时间复杂度为O(1)。最差情况:比较n次(共有n个元素),时间复杂度为O(n)。平均情况:综合两种情况,顺序查找的时间复杂度为O(n)。
索引顺序表查找算法:
(1)源代码
#include <stdio.h>
#define BLOCK_NUMBER 3
#define BLOCK_LENGTH 6
typedef struct IndexNode
{
int data; //数据
int link; //指针
}IndexNode;
//索引表
IndexNode indextable[BLOCK_NUMBER];
//块间查找
int IndexSequlSearch(int s[], int l, IndexNode it[], int key){
int i = 0;
while (key > it[i].data && i < BLOCK_NUMBER){
i++;
}
if (i > BLOCK_NUMBER){
return -1;
}
else{//在块间顺序查找
int j = it[i].link - 1;
while (key != s[j] && j < l) {
j++;
}
if (key == s[j]){
return j + 1;
}
else{
return -1;
}
}
}
//建立索引表
void IndexTable(int s[], int l, IndexNode indextable[]){
int j = 0;
for (int i = 0; i < BLOCK_NUMBER; i++){
indextable[i].data = s[j];
indextable[i].link = j;
for (j; j < indextable[i].link + BLOCK_LENGTH && j < l; j++){
if (s[j] > indextable[i].data){
indextable[i].data = s[j];
}
}
}
for (int i = 0; i < BLOCK_NUMBER; i++){
indextable[i].link++;
}
}
//打印查找的数据元素以及其在线索表中的位置
void print(int searchNumber, int index){
if (index == -1){
printf("查找元素:%d\n", searchNumber);
printf("查找失败!\n");
return;
}
else{
printf("查找元素:%d\n", searchNumber);
printf("元素位置:%d\n", index);
return;
}
}
int main(){
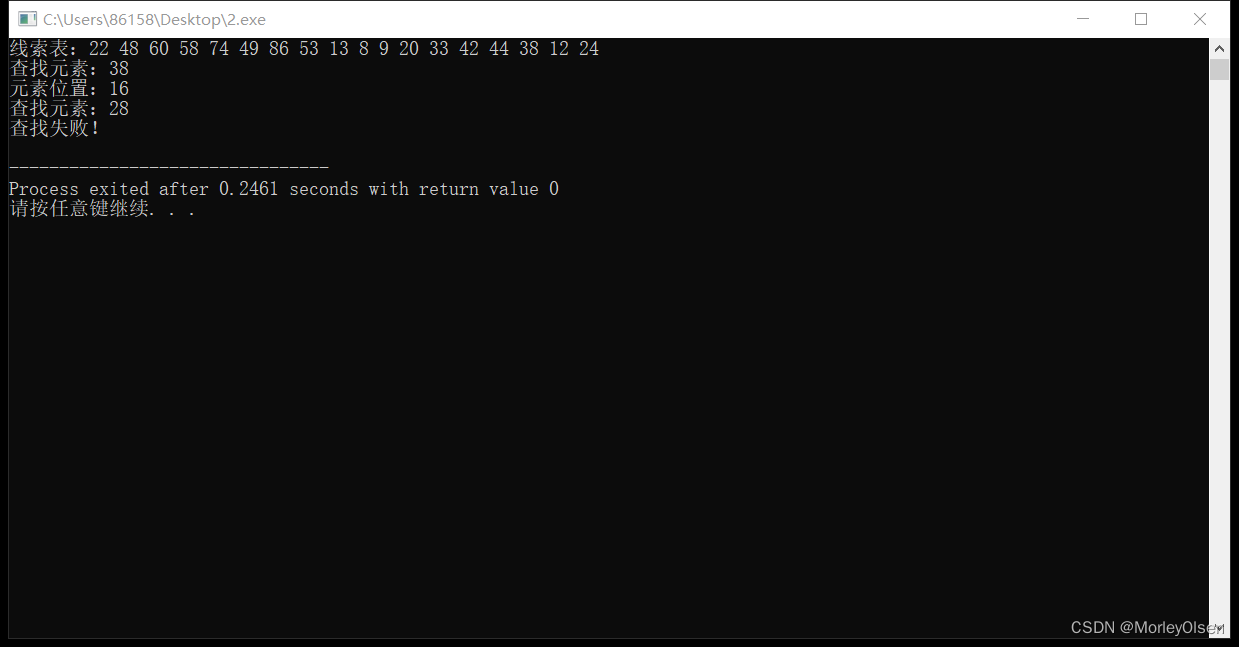
int s[18] = {22,48,60,58,74,49,86,53,13,8,9,20,33,42,44,38,12,24};
IndexTable(s, 18, indextable);
printf("线索表:");
for (int i = 0; i < 18; i++){
printf("%d ",s[i]);
}
printf("\n");
int indexNumber1 = 38;
int index1 = IndexSequlSearch(s, 18, indextable, indexNumber1);
print(indexNumber1, index1);
int indexNumber2 = 28;
int index2 = IndexSequlSearch(s, 18, indextable, indexNumber2);
print(indexNumber2, index2);
return 0;
}
(2)测试用例及其运行结果
(3)时间、空间复杂度分析
算法思想:
首先,将n个数据元素"按块有序"划分为m块(m ≤ n)。每一块中的结点不必有序,但块与块之间必须"按块有序";即后一块中任一元素都必须大于前一块中最大的元素;然后,块之间进行二分或者顺序查找,块内进行顺序查找。
时间复杂度:
整体算法是对顺序查找的改进,介于顺序查找和二分查找之间,时间复杂度为O(log2m+n/m)。
空间复杂度:
一般情况下,为进行分块查找,可以将长度为n的表均匀分成b块,每块还有s个元素,即b = [n/s]。索引表采用顺序查找的方式,则查找成功时的平均查找长度为:(s+b+2)/2。