栈和队列第二弹，完结篇

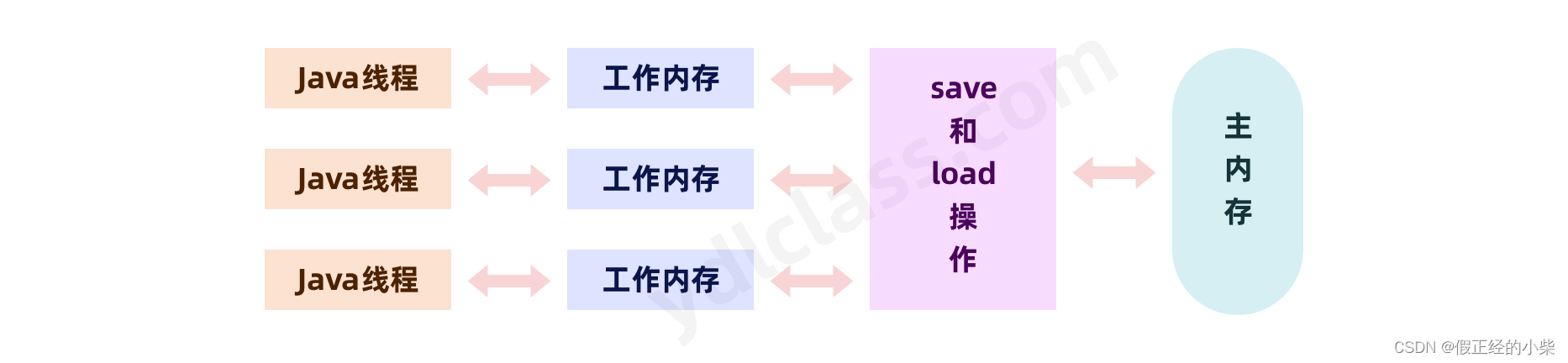
💛1.队列的基本底层实现

public class MyQueue {
    int array[];
    int usedsize=0;
    public MyQueue(){
        this.array=new int [5];
    }

💙2.判断是否满，满了需要扩容

Arrays.copyOf(数组，数组的长度）；我常常会忘记哈哈哈哈哈

 //判满
    public  void  ifFull(){
        if(usedsize==5)
        array=Arrays.copyOf(this.array,array.length*2);
    }

💜3.判断是否为空

 //是否为空
    public boolean isEmpty(){
        if(usedsize==0){
            return true;
        }
        return false;
    }

❤️4.添加元素

    //添加元素
    public void add(int data){
        ifFull();             //满了就扩容
        usedsize++;
        array[usedsize-1]=data;
    }

💚5.查找队首元素

 //查看队首元素
    public int  element(){
        return array[0];
    }

💓 6.出队

  //出队
    public int poll(){
        int m=array[0];
        for(int i=1;i<usedsize;i++){
            array[i-1]=array[i];
        }
        usedsize--;
        return array[0];
    }

💕7.遍历元素个数

//遍历队列元素
    public void display(){
        for(int i=0;i<usedsize;i++){
            System.out.println(array[i]);
        }
    }

栈的集合基本操作

offer(x);把x元素插入到队列里面

poll()：弹出栈顶元素，并且返回该值

其他与栈相同，peek,isEmpty,

注意还有一个size()这个方法也容易忽视。：返回队列数值

一、

💛

最小栈

1.说简单也很简单，就是可能在一些小细节方面进坑，比如说插入元素，就容易没想那么多，导致多插入一次;（🌚 🌚 🌚 又是一下午的经验之道）

简单讲一下我的思路点：刚开始肯定都是没思路，我就开始一个一个慢慢写，为什么是两个栈，因为他要求找到最小的元素要求时间复杂度是O（1），所以要有第二个栈，然后栈肯定，他需要有一定特殊性，才能出栈是最小的，但是他假如只有一个，那她最小的肯定就是他，所以最小栈肯定要入他，剩下的就要找还有什么类型的需要进来，

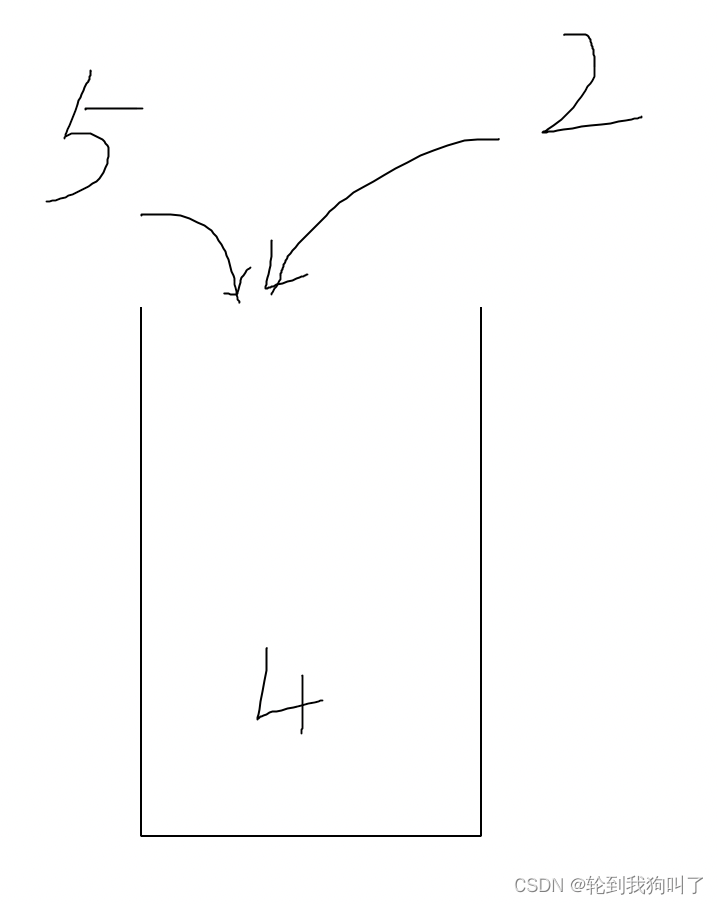
看下图👋，5和2，哪个应该进来，肯定是2应该进来，因为2小啊。我就是为了找最小值

，只有删除和新增有点难度，其余的就不谈了，没啥必要。

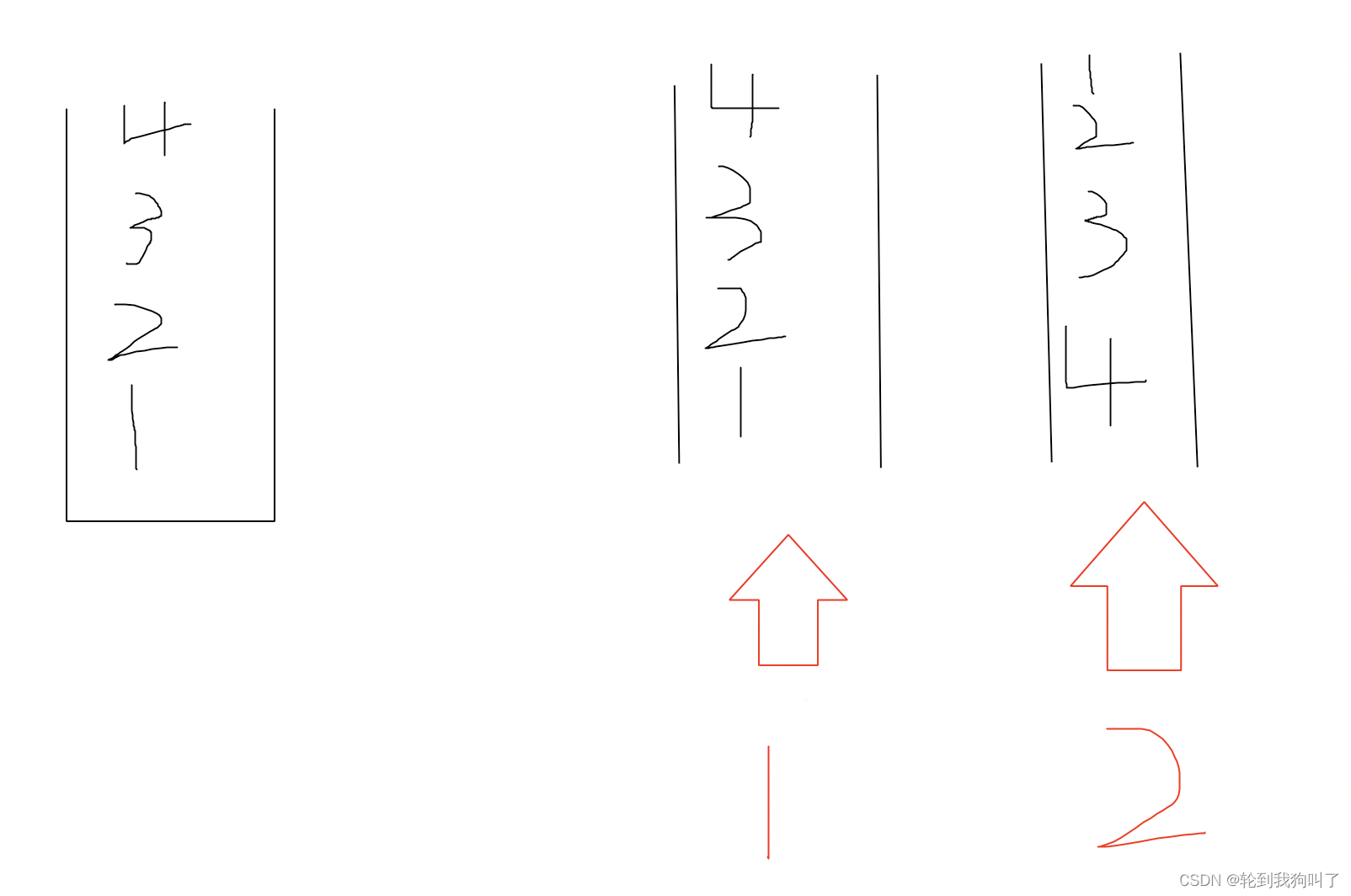
⭐️ 🌟 💫 还有一个问题你要想清楚，我们弹出栈的时候，最小栈应该怎么办，

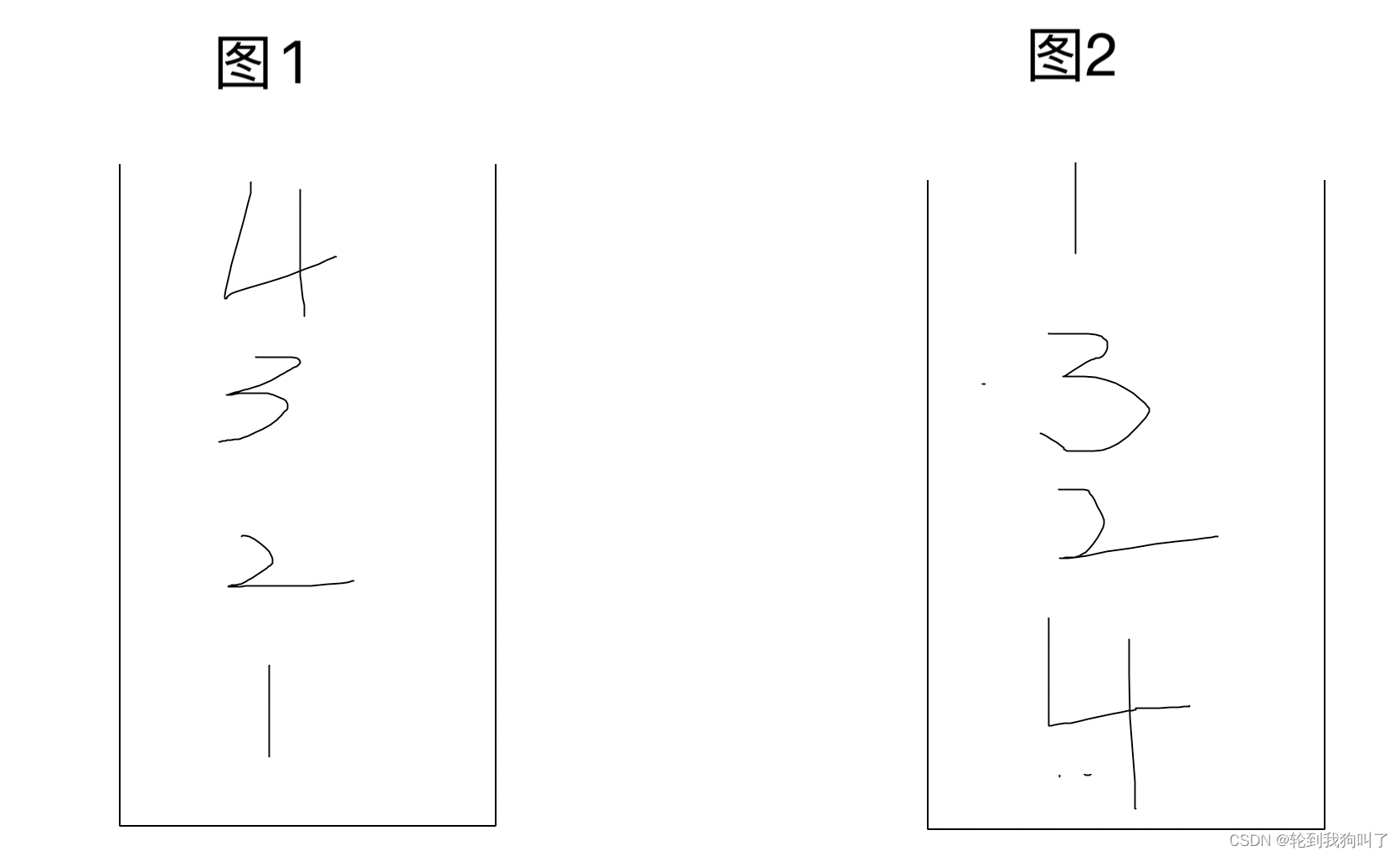
看下面图，假如是图1：他的最小栈应该是是只有1。图二应该是有1，2，4，

拿图2举例子，开始弹出1，然后最小栈的栈顶也是1，然后最小栈也开始弹，开始弹出3，然后最小栈的栈顶不是3，那么就原始栈弹，最小栈不弹，换句话说：一样就弹出，不一样的不用弹出。

class MinStack {
    private Stack<Integer> data;
    private Stack<Integer> minStack;
    public MinStack() {
          data=new Stack<>();
          minStack=new Stack<>();
    } 
    public void push(int val) {
        data.push(val);
    if(minStack.isEmpty()){
        minStack.push(val);
    }
    else if(minStack.peek()>=val){         //这个很关键，一定要是else 
        minStack.push(val);                //避免插入的时候，有可能进入一次这个，会再次插入
    } 
    }
    public void pop() {
        int pop=data.pop();
        int top=minStack.peek();
     if(pop==top){
           minStack.pop();
     }
    }
    public int top() {
        return data.peek();
    }
    public int getMin() {
       return minStack.peek();
    }
}

二、

💙

2.用队列实现栈：解法一通过一个栈，来实现，首先，一个栈的基本操作是压栈，弹栈，是否为空，返回栈顶操作（队列是进队从尾巴进，出队从头出）弹出栈顶也就是4，那么弹出4的话那么队列的队头也是4，他的弹栈操作就实现了，那么返回栈顶也实现了，空肯定也实现了，那么我们目前最大的问题就是如何把这个1队列逆置过来，让他变成2的：1，2，3，4呢。

把它用递归的想法去想，他只有一个队列，然后只有一个的时候，不逆置（size在插入之前的个数），所以从i=0;size=0刚开始为1开始，假如插入一个size停留在插入之前也就是1，也相对应他需要调整逆置一次，重新吧1插入，形成:2，1 💗 1，2的逆置变化。然后当他是3的时候（1，2，需要被逆置）所以，（注意哈，❗️❗️❗️他并不是从3，2，1开始换，而是从3，1，2开始换，）只需要换两次。～～～以此类推。

class MyStack {
    Queue<Integer>stack1;
  
    public MyStack() {
    stack1=new LinkedList<Integer>();
      
    }
    
    public void push(int x) {
        int n=stack1.size();
         stack1.offer(x);
        for (int i = 0; i < n; i++) {
            stack1.offer(stack1.poll());
        }
    }
    
    public int pop() {
        return stack1.poll();
    }
    
    public int top() {
       
     return stack1.peek();

    }
    
    public boolean empty() {
    return stack1.isEmpty();
    }
}

💚

解法2:

用两个队列：两个队列就是思路是先从出队和入队开始思考，假如说要出队，那么就需要把除了队尾元素以外的全部拿出来，放到那个空的队列中，然后剩下的一个就是队尾（也就是要出的栈顶），那么插入的时候：我们就需要看哪个是空的，哪个里面有数，假如说里面有东西，就插入非空的队列（里面有东西的），要是两个都是空，那么随便插入一个。

class MyStack{ 
        Queue<Integer>stack1;
        Queue<Integer> stack2;
        public MyStack() {
            stack1=new LinkedList<Integer>();
            stack2=new LinkedList<Integer>();
        }
        public void push(int x) {
            if((stack1.isEmpty())&&!(stack2.isEmpty())){
                stack2.offer(x);
            }
            if(!(stack1.isEmpty())&&(stack2.isEmpty())){
                stack1.offer(x);
            }
             if(stack1.isEmpty()&&stack2.isEmpty()){
                stack1.offer(x);
            }
        }

        public int pop() {
            if((stack1.isEmpty())&&(!stack2.isEmpty())){
                int a=stack2.size();
                while(a>1){
                    stack1.offer(stack2.poll());
                    a--;                   //除了最后一个，全部移动到另一个队列中
                }
                return stack2.poll();     //删除
            }
            else   if((!stack1.isEmpty())&&(stack2.isEmpty())){
                int a=stack1.size();
                while(a>1){
                    stack2.offer(stack1.poll());
                    a--;
                }
                return stack1.poll();
            }
            else{ return -1; }
        }

        public int top() {
            if((stack1.isEmpty())&&(!stack2.isEmpty())){
                int a=stack2.size();
                while(a>1){
                    stack1.offer(stack2.poll());
                    a--;
                }
                int c=stack2.peek();         //最后一个剩余的元素，需要存起来，放回到和其他元素在一起
                stack2.poll();
                stack1.offer(c);
                return c;
            }
            if((!stack1.isEmpty())&&(stack2.isEmpty())){
                int a=stack1.size();
                while(a>1){
                    stack2.offer(stack1.poll());
                    a--;
                }
                int c=stack1.peek();
                stack1.poll();
                stack2.offer(c);
                return c;
            }
            else {
                return -1;
            }
        }
        public boolean empty() {
            return stack1.isEmpty()&&stack2.isEmpty();       //两个都是空，才真正是空
        }
    }

三、

💜

用栈实现队列和，大体和用队列实现栈的思想相同，但是我们这里面定义了一个m，他的含义是什么呢，因为假如我们插入，删除，取栈顶的时候情况不同。假如删除和取栈顶的操作，需要把栈中的元素全逆置出来，如果我们删除了，就不用再需要取栈顶时候逆置。但是当我们插入的时候有需要把原本逆置的元素给他恢复到正常状态，这样他才可以进行正常的插入，不影响他的顺序。后续假如再去删除接着逆置就好了，所以我们这里定义一个m，m开始为0，偶数默认有序，奇数认为进行了逆序操作，push是如果正常直接插入，不正常的话奇数，开始一个逆序把它变为正常💫💫💫（要注意这个m不++）因为把它变到正常序了，下一个要进行的操作还是需要逆序

class MyQueue {
    Stack<Integer> stack1;
    Stack <Integer>stack2;

    int m=0;
    public MyQueue() {
        stack1=new Stack<>();
        stack2=new Stack<>();
    }

    public void push(int x) {
        if(m%2==0) {
            if ((stack1.isEmpty()) && !(stack2.isEmpty())) {
                stack2.push(x);
            }
            if (!(stack1.isEmpty()) && (stack2.isEmpty())) {
                stack1.push(x);
            }
        }
        if(m%2!=0){
            if((stack1.isEmpty())&&(!stack2.isEmpty())){
                int a=stack2.size();
                while(a>0){
                    stack1.push(stack2.pop());
                    a--;
                }
                m++;
                stack1.push(x);
            }
            else   if((!stack1.isEmpty())&&(stack2.isEmpty())){
                int a=stack1.size();
                while(a>0){
                    stack2.push(stack1.pop());
                    a--;
                }
                m++;
                stack2.push(x);
            }
            }
        if (stack1.isEmpty() && stack2.isEmpty()) {
            stack1.push(x);
        }
    }
    public int pop() {
        if(m%2!=0){
            if((stack1.isEmpty())&&(!stack2.isEmpty())){
                return stack2.pop();
            }
            if((!stack1.isEmpty())&&(stack2.isEmpty())){
                return stack1.pop();
            }
        }
        if(m%2==0){
            if((stack1.isEmpty())&&(!stack2.isEmpty())){
                int a=stack2.size();
                while(a>1){
                    stack1.push(stack2.pop());
                    a--;                   //除了最后一个，全部移动到另一个队列中
                }
                m++;
                return stack2.pop();     //删除
            }
            else   if((!stack1.isEmpty())&&(stack2.isEmpty())){
                int a=stack1.size();
                while(a>1){
                    stack2.push(stack1.pop());
                    a--;
                }
                m++;
                return stack1.pop();
            }
        }
        return -1;
    }
    public int peek() {
        if(m%2!=0){
            if((stack1.isEmpty())&&(!stack2.isEmpty())){
                return stack2.peek();
            }
            if((!stack1.isEmpty())&&(stack2.isEmpty())){
                return stack1.peek();
            }
        }
        if(m%2==0) {
            if ((stack1.isEmpty()) && (!stack2.isEmpty())) {
                int a = stack2.size();
                while (a > 1) {
                    stack1.push(stack2.pop());
                    a--;

                }
                m++;
                int c = stack2.peek();         //最后一个剩余的元素，需要存起来，放回到和其他元素在一起
                stack2.pop();
                stack1.push(c);
                return c;
            }
            if ((!stack1.isEmpty()) && (stack2.isEmpty())) {
                int a = stack1.size();
                while (a > 1) {
                    stack2.push(stack1.pop());
                    a--;

                }
                m++;
                int c = stack1.peek();
                stack1.pop();
                stack2.push(c);
                return c;
            }
        }
            return -1;
    }
    public boolean empty() {
        return stack1.isEmpty()&&stack2.isEmpty();
    }
}

四、设计循坏队列

⭐️⭐️⭐️

首先设计循环队列，我们要清楚什么是循环队列以及他出现的意义

🌋🌋🌋1.为了解决假溢出问题（front在q号位置，rear在m号位置）就叫假溢出，因为正常队列这个时候存不了，所以才有循环队列。（假溢出的原因是由于弹栈导致会使front向前移动）

⛅️⛅️⛅️2.不是说他可以无限插入无数个数，而是她可以满了后，覆盖前面的数据

❗️❗️循环队列的特性是（有一个空间，他是不用来存东西，而是区分判断他是空还是满，从而彻底解决假溢出（满就是(rear+1)%capaciy(容量k+1)==front

🎥🎥🎥

其次不要忘了，他的本质还是队列，插入完成rear++; 删除是front++。（但是这个题，他不允许，满的时候就不可以插入了）

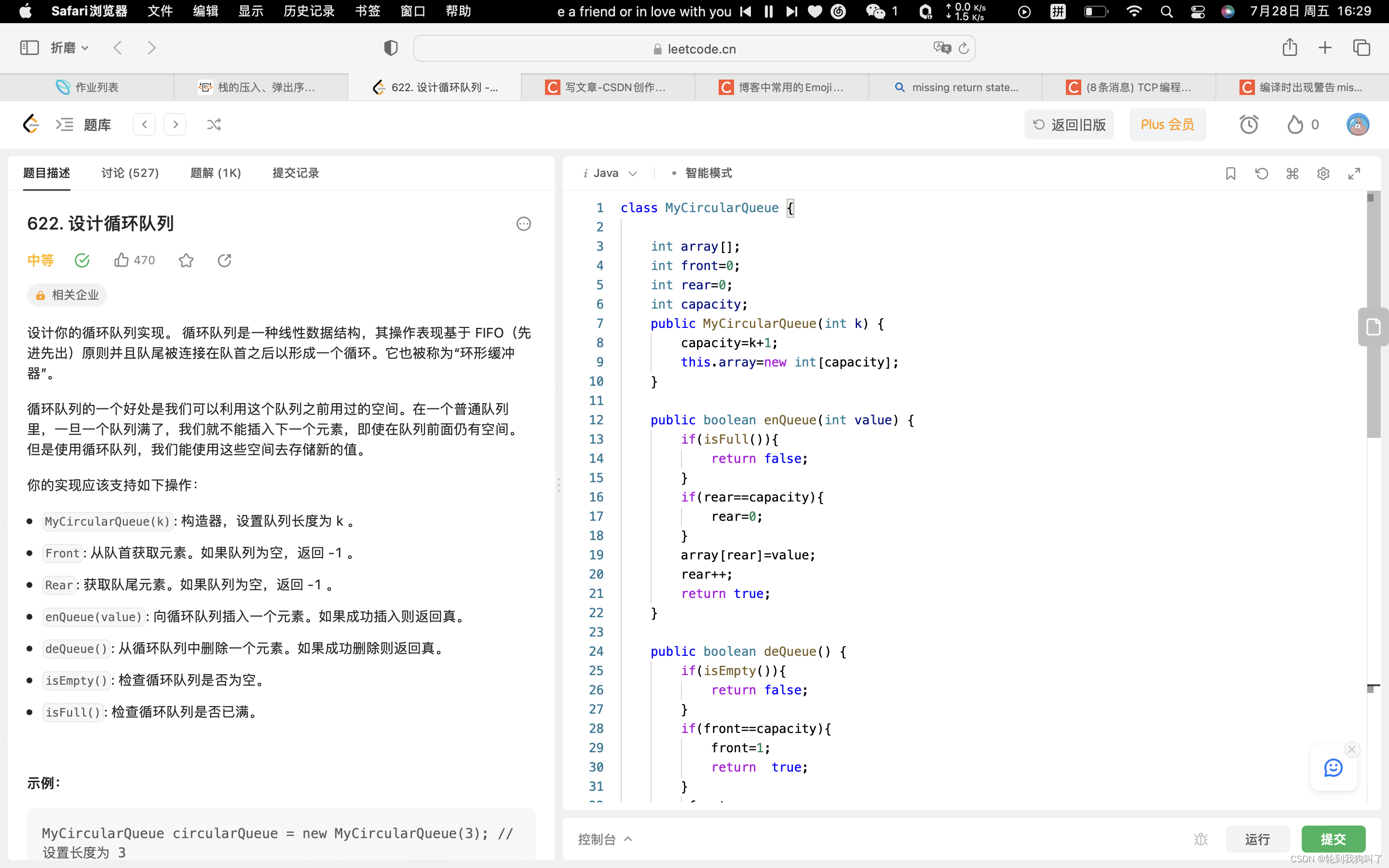
class MyCircularQueue {

    int array[];
    int front=0;
    int rear=0;
    int capacity;
    public MyCircularQueue(int k) {
        capacity=k+1;
        this.array=new int[capacity];
    }

    public boolean enQueue(int value) {
        if(isFull()){
            return false;
        }
        if(rear==capacity){            //如果这时候相等，但还不是满，就说明是假溢出
            rear=0;                    //此时吧rear放到0开始，（front没占的空间）
        }
        array[rear]=value;
        rear++;                    
        return true;
    }

    public boolean deQueue() {
        if(isEmpty()){
            return false;
        }
        if(front==capacity){          //假溢出，此时要删除，直接front跳到1，把0号删除
            front=1;
            return  true;         
        }
         front++;
        return true;
    }

    public int Front() {
        if(isEmpty()){
            return -1;
        }
        return array[front];
    }

    public int Rear() {
        if(isEmpty()){
            return -1;
        }

        return array[rear-1];
    }

    public boolean isEmpty() {
        if(front==rear){
            return true;
        }
        return false;
    }

    public boolean isFull() {
        if((rear+1)%(capacity)==front){                //不行就记，能理解更好
            return true;
        }
        return false;
    }
}

一个比较不好理解的，弹栈中

if(front==capacity){ //假溢出，此时要删除，直接front跳到1，把0号删除
front=1;
return true;
}

也就是这种情况，front需要跳过到0的位置，如果rear是0不就是null了吗，就不会弹栈了

五、

💥💥💥

判断是不是栈的压入，弹出的序列：我们在想的时候很好想，但是具体如何写成代码的时候，就有些问题了。

解法：将给的序列，压入到栈里面，然后看弹出栈的序列和栈顶元素是否相同。假如说相同，那么进行弹栈，假如说不相同就把这个元素添加进入栈里面

那么这里说一点细节，光看上面肯定会有一些小疑惑：

那么首先是一边判断一边压入，他需要判断，从哪里开始出栈，假如说匹配上就说明，从这个点开始出栈了

其次空了，他就直接插入就行，

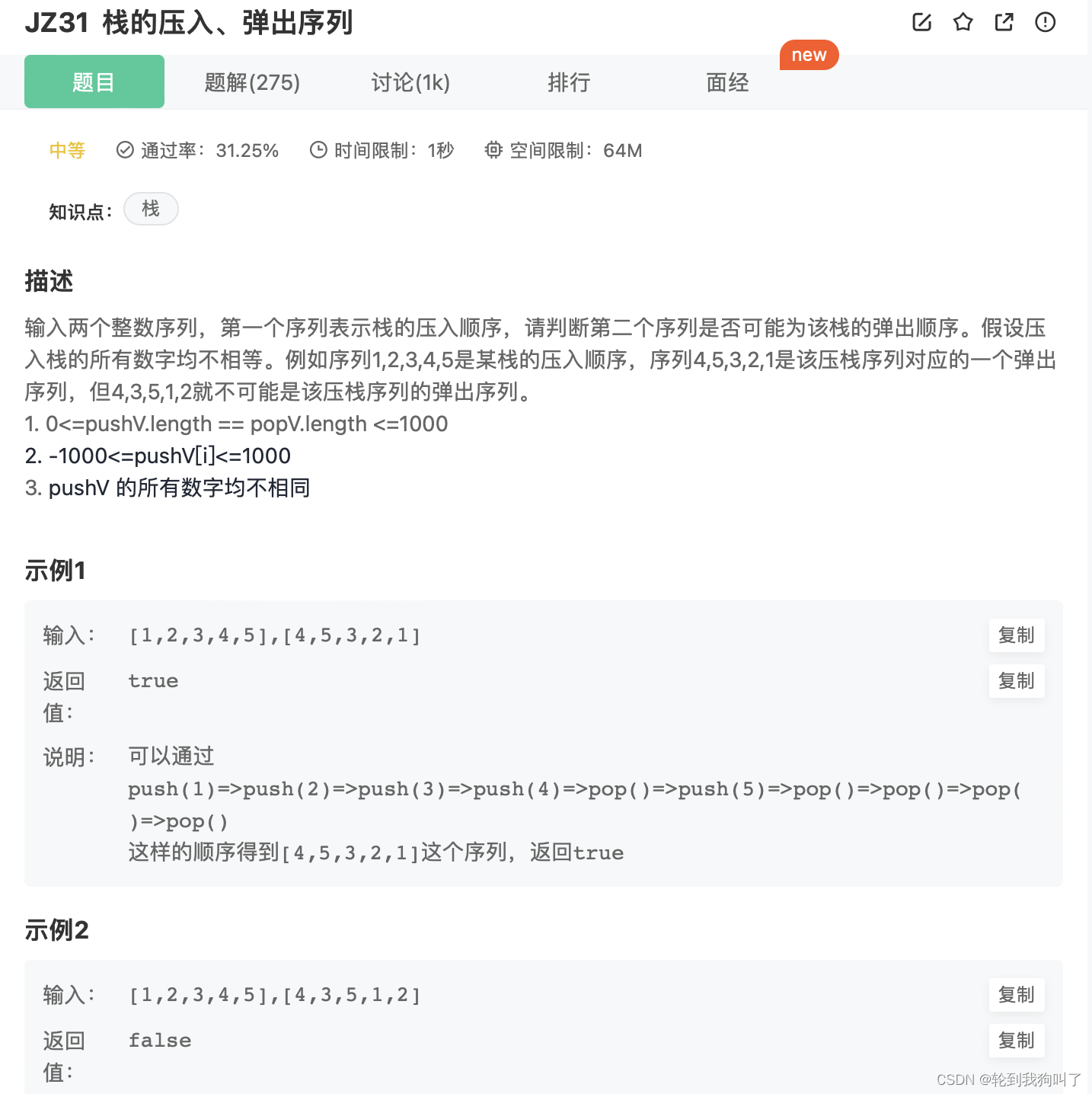
public boolean IsPopOrder (int[] pushV, int[] popV) {
        // write code here
       Stack <Integer>stack1=new Stack<>();
       int i=0;
       for(int j=0;j<pushV.length;j++){
       while(i<pushV.length&&(stack1.isEmpty()||popV[j]!=stack1.peek())){
       stack1.push(pushV[i]);             //遍历去寻找，有没有和栈顶相同的序列元素，
       i++;                                   
       }
       if(!stack1.isEmpty()&&popV[j]==stack1.peek()) 
         stack1.pop();                         
       else
        return false;
       }
       return true;
    }