1、样本不均衡定义

一般在分类机器学习中，每种类别的样本是均衡的，也就是不同目标值的样本总量是接近的，但是在很多场景下的样本没有办法做到理想情况，甚至部分情况本身就是不均衡情况：
（1）很多场景下，数据集本身不平和，部分类别的数据多于其他数据；
（2）固定场景下，例如风控的场景，负样本的比例远远小于正样本的占比；
（3）梯度下降过程中，不同类别的样本量比较大时，模型本身很难做到收敛最优解。

2、解决方案

不同场景下，对样本不均衡的解决方案侧重点不同，下面以金融风控举例：
（1）下探法：将被拒绝的用户放进来，充当负样本。缺点也很明显，容易风险高，成本也较高；
（2）代价敏感：对少数样本进行加权处理，让模型进行均衡训练；
（3）采样法：通过多正样本进行欠采样，或者负样本进行过采样的方式平衡样本；
（4）半监督学习

2.1 代价敏感

通过改变少数样本的权重，从而让模型得到一定的均衡训练。但是代价敏感加权增大了负样本在模型中的贡献度，但本身并没有为模型增加额外的信息，这就没有办法解决选择偏误的问题，也没办法带来负面影响。
在逻辑回归中就可以通过参数class_weight='balanced’来调整正负样本的权重，我们以逻辑回归评分卡为例，调整逻辑回归的class_weight的参数，看看结果，该例子链接：逻辑回归评分卡

# 导入模块
import pandas as pd
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import roc_auc_score,roc_curve,auc

data = pd.read_csv('Bcard.txt')
feature_lst = ['person_info','finance_info','credit_info','act_info']
# 划分数据
train = data[data.obs_mth != '2018-11-30'].reset_index().copy()
val = data[data.obs_mth == '2018-11-30'].reset_index().copy()
x = train[feature_lst]
y = train['bad_ind']
val_x = val[feature_lst]
val_y = val['bad_ind']

# 查看正负样本的数量
print('训练集：\n',y.value_counts())
print('跨时间验证集：\n',val_y.value_counts())

# 训练模型
lr_model = LogisticRegression(C=0.1)
lr_model.fit(x,y)

# 训练集
print('参数调整前的ks值')
y_pred = lr_model.predict_proba(x)[:,1] #取出训练集预测值
fpr_lr_train,tpr_lr_train,_ = roc_curve(y,y_pred) #计算TPR和FPR
train_ks = abs(fpr_lr_train - tpr_lr_train).max() #计算训练集KS
print('train_ks : ',train_ks)

#验证集
y_pred = lr_model.predict_proba(val_x)[:,1] #计算验证集预测值
fpr_lr,tpr_lr,_ = roc_curve(val_y,y_pred) #计算验证集预测值
val_ks = abs(fpr_lr - tpr_lr).max() #计算验证集KS值
print('val_ks : ',val_ks)


# 调整逻辑回归中的class_weight参数
print('参数调整后的ks值')
lr_model = LogisticRegression(C=0.1,class_weight = 'balanced')
lr_model.fit(x,y)
y_pred = lr_model.predict_proba(x)[:,1] #取出训练集预测值
fpr_lr_train,tpr_lr_train,_ = roc_curve(y,y_pred) #计算TPR和FPR
train_ks = abs(fpr_lr_train - tpr_lr_train).max() #计算训练集KS
print('train_ks : ',train_ks)
y_pred = lr_model.predict_proba(val_x)[:,1] #计算验证集预测值
fpr_lr,tpr_lr,_ = roc_curve(val_y,y_pred) #计算验证集预测值
val_ks = abs(fpr_lr - tpr_lr).max() #计算验证集KS值
print('val_ks : ',val_ks)

在这里插入图片描述
从上面可以看出，调整参数后的训练集合验证集的ks值都有了一定的提升。

2.2 过采样

代价敏感有用，但效果不一定，通过对负样本进行过采样能够达到更好的效果，即为模型引入更多的负样本。一般过采样的方法如下：

随机过采样：直接复制负样本，模型的泛化能力较差。
SMOTE算法：少数类别过采样技术（Synthetic Minority Oversampling Technique）

SMOTE过采样

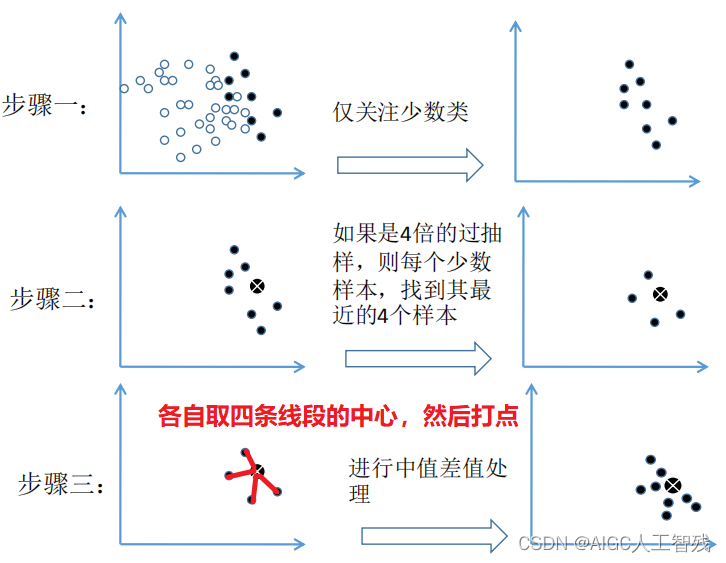
SMOTE是通过合成少数样本的过采样技术，它是通过对少数样本进行分析，然后在现有少数样本之间进行插值，人工合成新样本，合并样本到模型中训练。基本步骤如下：
（1）采用knn算法，计算出每个少数样本的k个近邻；
（2）从k个近邻中随机挑选N个样本进行随机线性插值；
（3）构造新的少数样本；
（4）将新样本和原本数据合并，产生新的训练集。
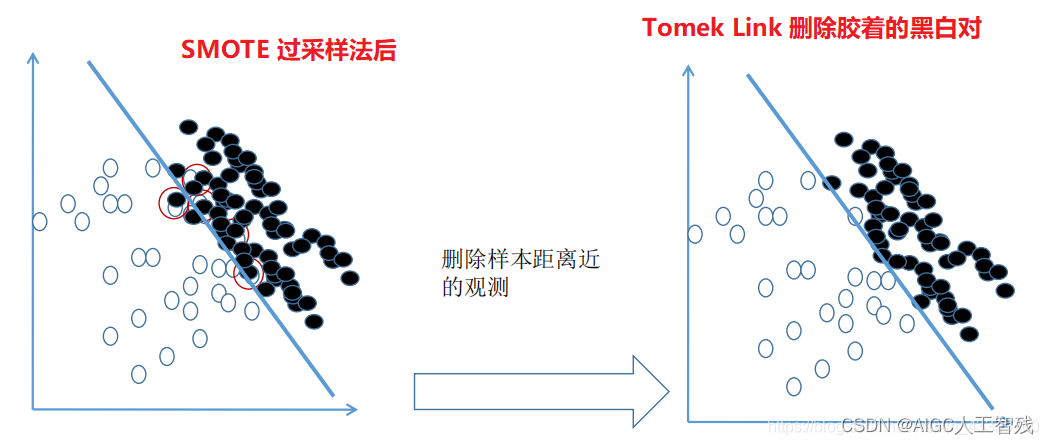
在这里插入图片描述

SMOTETomek综合采样

先使用过采样，扩大样本后再对处在胶着状态的点用 Tomek Link 法进行删除，有时候甚至连 Tomek Link 都不用，直接把离得近的对全部删除，因为在进行过采样后，0 和 1 的样本量已经达到了 1:1。
在这里插入图片描述

随机过采样、SMOTE采样和综合采样的示例代码

以上面的评分卡数据为例，读取数据的代码省略。
导入模块

from imblearn.over_sampling import RandomOverSampler,SMOTE
from imblearn.combine import SMOTETomek

使用三种过采样方法进行采样

# 随机过采样
ros = RandomOverSampler(random_state=0, sampling_strategy='auto')
x_ros, y_ros = ros.fit_resample(x,y)
print('随机过采样后分类情况：',y_ros.value_counts())

# SMOTE过采样
sot = SMOTE(random_state=0)
x_sot,y_sot = sot.fit_resample(x,y)
print('smote过采样后情况：',y_sot.value_counts())

# SMOTETomek综合采样
sttk = SMOTETomek(random_state=0)
x_sttk,y_sttk = sttk.fit_resample(x,y)
print('综合采样后情况：',y_sttk.value_counts())

在这里插入图片描述
比较三种采样后的ks值、recall值和auc值

data = [['原始数据',x,y],['随机过采样',x_ros,y_ros],['SMOTE过采样',x_sot,y_sot],['综合过采样',x_sttk,y_sttk]]

# 使用逻辑回归分别对过采样后的数据进行训练，看看情况
lr = LogisticRegression(C=0.1)
for text,train_X, train_y in data:
    lr.fit(train_X, train_y)
    y_pred = lr.predict_proba(val_x)[:,1] #计算验证集预测值
    pred_y = lr.predict(val_x)
    rc_score = recall_score(val_y,pred_y)
    fpr_lr,tpr_lr,_ = roc_curve(val_y,y_pred) #计算验证集预测值
    val_ks = abs(fpr_lr - tpr_lr).max() #计算验证集KS值
    auc_score = auc(fpr_lr,tpr_lr)
    print(text,'ks',val_ks,'auc',auc_score,'recall',rc_score)

在这里插入图片描述
以上可以看出三种方法过采样可以提升模型的评分，但没有一定要采用哪种过采样方法，不同的数据会有不同的情况。

机器学习与过采样

我们还能使用机器学习先对训练集的数据进行拟合，将预测结果较差的样本排除，不参与过采样，具体代码如下：
这里我们使用lightGBM算法，数据还是使用上面数据

 # 使用lightGBM进行数据拟合，去掉预测结果较差的数据，再进行smote过采样
import lightgbm as lgb
import numpy as np
lgb_clf = lgb.LGBMClassifier(learning_rate=0.05,n_estimators=100)
lgb_clf.fit(x, y, eval_set=[(x, y), (val_x, val_y)], eval_metric='auc')
temp = x.copy()
temp['bad_ind'] = y
temp['pred'] = lgb_clf.predict_proba(x)[:,1]
temp=temp.sort_values(by=['pred'], ascending=False).reset_index()
temp['rank'] = np.array(temp.index)/len(temp)
temp

在这里插入图片描述
我们定义一个weight函数，将预测不准的前后各20%数据排除

def weight(x,y):
    if x==0 and y<0.2:
        return 0.1
    elif x==1 and y>0.8:
        return 0.1
    else:
        return 1
    
temp['weight'] = temp.apply(lambda x:weight(x.bad_ind,x['rank']), axis=1)
smote_sample = temp[temp.weight==1]
print(smote_sample.shape)
train_X_smote = smote_sample[feature_lst]
train_y_smote = smote_sample['bad_ind']

在这里插入图片描述
同样进行三种采样，跟没有采样数据进行对比

# 随机过采样
ros = RandomOverSampler(random_state=0, sampling_strategy='auto')
x_ros, y_ros = ros.fit_resample(train_X_smote,train_y_smote)
print('随机过采样后分类情况：',y_ros.value_counts())

# SMOTE过采样
sot = SMOTE(random_state=0)
x_sot,y_sot = sot.fit_resample(train_X_smote,train_y_smote)
print('smote过采样后情况：',y_sot.value_counts())

# SMOTETomek综合采样
sttk = SMOTETomek(random_state=0)
x_sttk,y_sttk = sttk.fit_resample(train_X_smote,train_y_smote)
print('综合采样后情况：',y_sttk.value_counts())

data = [['原始数据',x,y],['随机过采样',x_ros,y_ros],['SMOTE过采样',x_sot,y_sot],['综合过采样',x_sttk,y_sttk]]

# 使用逻辑回归分别对过采样后的数据进行训练，看看情况
lr = LogisticRegression(C=0.1)
for text,train_X, train_y in data:
    lr.fit(train_X, train_y)
    y_pred = lr.predict_proba(val_x)[:,1] #计算验证集预测值
    pred_y = lr.predict(val_x)
    rc_score = recall_score(val_y,pred_y)
    fpr_lr,tpr_lr,_ = roc_curve(val_y,y_pred) #计算验证集预测值
    val_ks = abs(fpr_lr - tpr_lr).max() #计算验证集KS值
    auc_score = auc(fpr_lr,tpr_lr)
    print(text,'ks',val_ks,'auc',auc_score,'recall',rc_score)