Problem - 7322

题目大意：有一个n个点的边权有向图，求图中环的权的最小值以及相应最小环的数量

1<=n<=500

思路：要求一个如下图的环的大小，我们只需知道u到v的最短路径加上v到u的边权

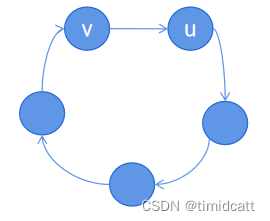
这样的话我们需要求出任意两点之间的最短路，再枚举边即可，所以用到floyd算法，我们在每次路径更新时，或者找到权值相同的路径时，都要维护最短路径的数量cnt，然后在每次第k个点更新完成后，可以直接枚举小于k的点i与k之间的边，如果有环，就判断以k为顶点的环：ma[i][k]+dis[k][i]是不是最小值，如果是最小值相等，也要更新数量

#include<__msvc_all_public_headers.hpp>
//#include<bits/stdc++.h>
using namespace std;
const int N = 505;
typedef long long ll;
const ll INF = 1e14;
ll ma[N][N];
ll dis[N][N];
ll cnt[N][N];
ll ans1 = INF;
const ll MOD = 998244353;
int n, m;
ll ans2 = 0;
void init()
{//初始化
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= n; j++)
		{
			ma[i][j] = 0;
			dis[i][j] = INF;
			cnt[i][j] = 0;
		}
		dis[i][i] = 0;
		cnt[i][i] = 0;//没有自环
	}
	ans1 = INF;
	ans2 = 0;
}
void floyd()
{
	for (int k = 1; k <= n; k++)
	{
		for (int i = 1; i <= n; i++)
		{
			for (int j = 1; j <= n; j++)
			{
				if (dis[i][j] > dis[i][k] + dis[k][j])
				{//更新最短路
					dis[i][j] = dis[i][k] + dis[k][j];
					cnt[i][j] = cnt[i][k] * cnt[k][j] % MOD;//更新最短路条数
				}
				else if (dis[i][j] == dis[i][k] + dis[k][j])
				{//与最短路相等也要维护数量
					cnt[i][j] = (cnt[i][j] + cnt[i][k] * cnt[k][j] % MOD) % MOD;
				}
			}
		}
		for (int i = 1; i <= k - 1; i++)
		{//枚举已经更新好的顶点
			if (ma[k][i])
			{
				if (ma[k][i] + dis[i][k] < ans1)
				{//当前环更小
					ans1 = ma[k][i] + dis[i][k];
					ans2 = cnt[i][k];
				}
				else if (ma[k][i] + dis[i][k] == ans1)
				{//与最小环等长
					ans2 = (ans2 + cnt[i][k]) % MOD;
				}
			}
		}
	}
}
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	int t;
	cin >> t;
	while (t--)
	{
		cin >> n >> m;
		init();
		for (int i = 1; i <= m; i++)
		{
			int u, v;
			ll w;
			cin >> u >> v >> w;
			ma[u][v] = w;
			cnt[u][v] = 1;
			dis[u][v] = w;
		}
		floyd();
		if (ans1 == INF)
		{
			cout << -1 << " " << -1 << endl;
		}
		else
		{
			cout << ans1 << " " << ans2 << endl;//题目描述的不清楚，路径长度是不能取模的
		}
	}
	return 0;
}