1、概述

SM4分组密码算法是一种迭代分组密码算法，采用非平衡Feistel结构，分组长度为128bit，
①Z₂^e表示e-比特的向量集，Z₂³²中的元素称为字，Z₂⁸中的元素称为字节
②S盒为固定的8bit输入8bit输出的置换，记为Sbox()
③⊕表示2bit异或；<<<i表示32bit循环左移i位
④密钥及密钥参量
加密密钥长度位128bit，表示MK=(MK₀,MK₁,MK₂,MK₃)，分别是字。
轮密钥rk是由加密密钥生成。
FK是系统参数，CK是固定参数，用于密钥扩展算法。

1.1初始变量算法

反序变换为R(A0,A1,A2,A3)=(A3,A2,A1,A0)
算法的加密变换为：X_i+4=F(X_i,X_i+1,X_i+2,X_i+3,rk_i)=X_i⊕T(X_i+1i⊕X_i+2i⊕X_i+3i⊕rk_i)
(Y₀,Y₁,Y₂,Y₃)=R(X₃₂,X₃₃,X₃₄,X₃₅)=(X₃₅,X₃₄,X₃₃,X₃₂)
其中，F是轮函数，T是合成置换
加解密的结构相同，但是轮密钥的使用顺序不一样，加密的时候是0-31，解密的时候是31-0
加密流程图如下：

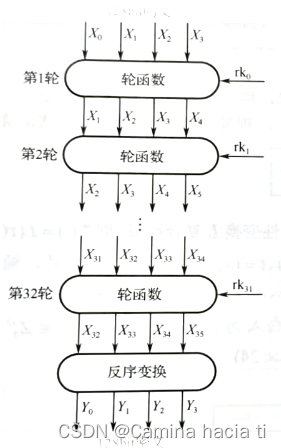
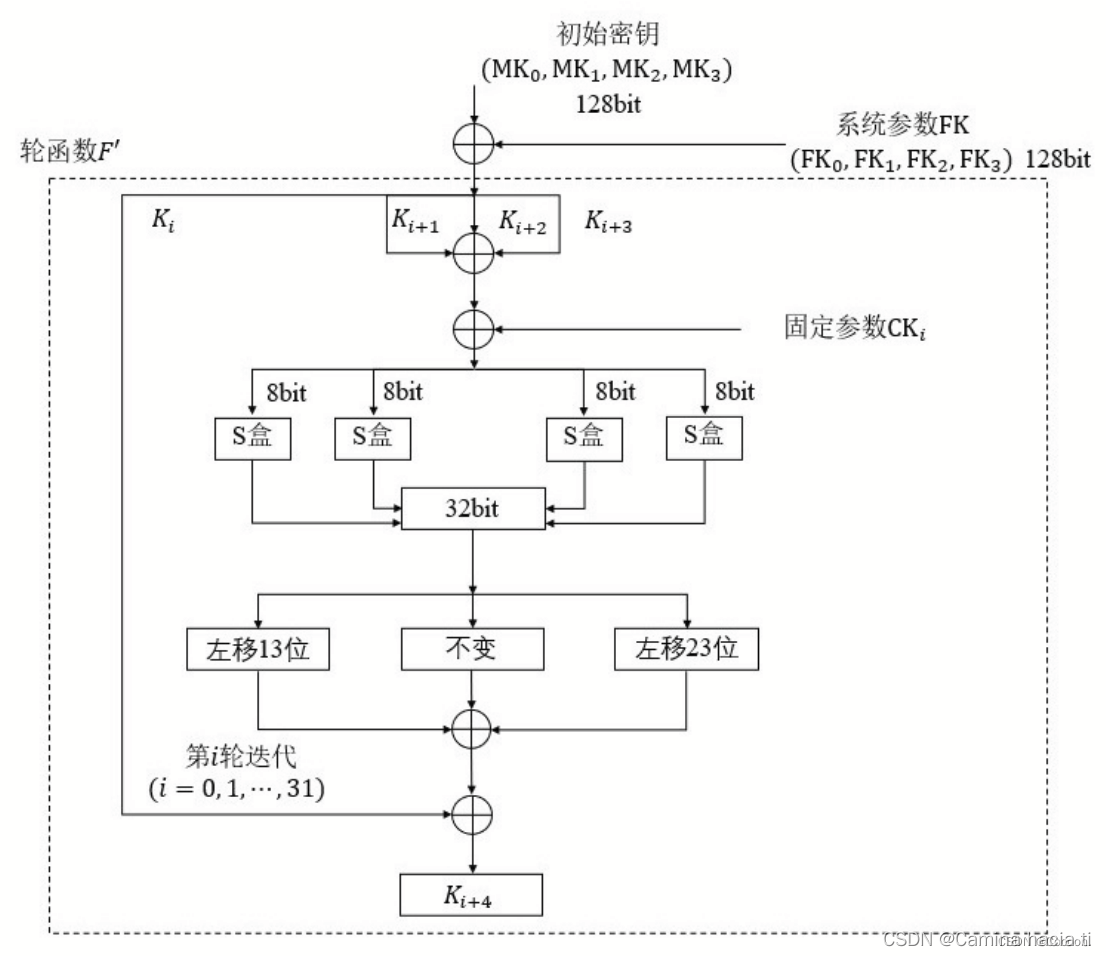
轮函数如图：

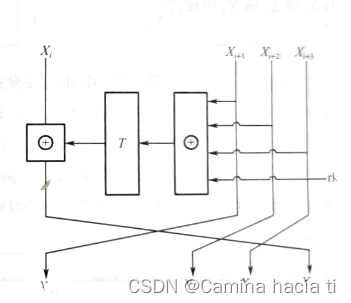
1.2密钥扩展算法

轮密钥生成方法：

(K₀，K₁，K₂，K₃) = (MK₀⊕FK₀，MK₁⊕FK₁，MK₂⊕FK₂，MK₃⊕FK₃)

rki=K(i+4) = Ki⊕T’（K_i+1)⊕K_i+2⊕K_i+3⊕CK_i）
T’变换与加密算法轮函数的T基本相同，只是将线性变换L变成L’，也就是：
　L’(B)=B⊕(B<<<13)⊕(B<<<23)

常数FK的值：
FK₀=（A3B1BAC6）
FK₁=（56AA3350）
FK₂=（677D9197）
FK₃=（B27022DC）
固定参数CK的取值：
一共使用有32个固定参数CK_i，CK_i，是一个字，它的产生规则是：

设ck_i，j为CK_i的第j字节(i=0，1，…，31;j=0,1,2,3)，即CK_j=(ck_i,0,ck_i,1,ck_i,2,ck_i,3),

则 ck_i，j=(4i+j)×7(mod 256)
下面是32个固定参数CK的十六进制表示形式的具体值：

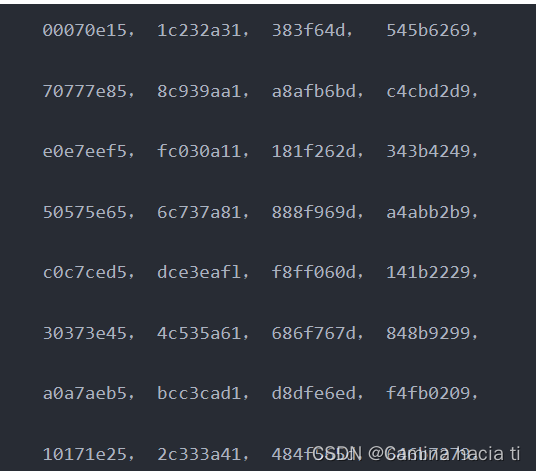
1.3轮函数F

算法采用非线性迭代结构，以字为单位进行加密运算，称一次迭代运算为一轮变换。
F（X₀,X₁,X₂,X₃)=X₀⊕T(X₁⊕X₂⊕X₃⊕rk₀)

1.3.1合成置换T

T是一个可逆变换，由非线性变换τ和线性变换L复合而成，即T(·)=L(r(·))
非线性变换r由4个并行的S盒组成，输出b_i，输入a_i，则b_i=Sbox(a_i)
非线性变换r的输出是线性变换L的输入。输出C，输入B，则
C=L(B)=B⊕(B<<<2)⊕(B<<<10)⊕(B<<<18)⊕(B<<<24)

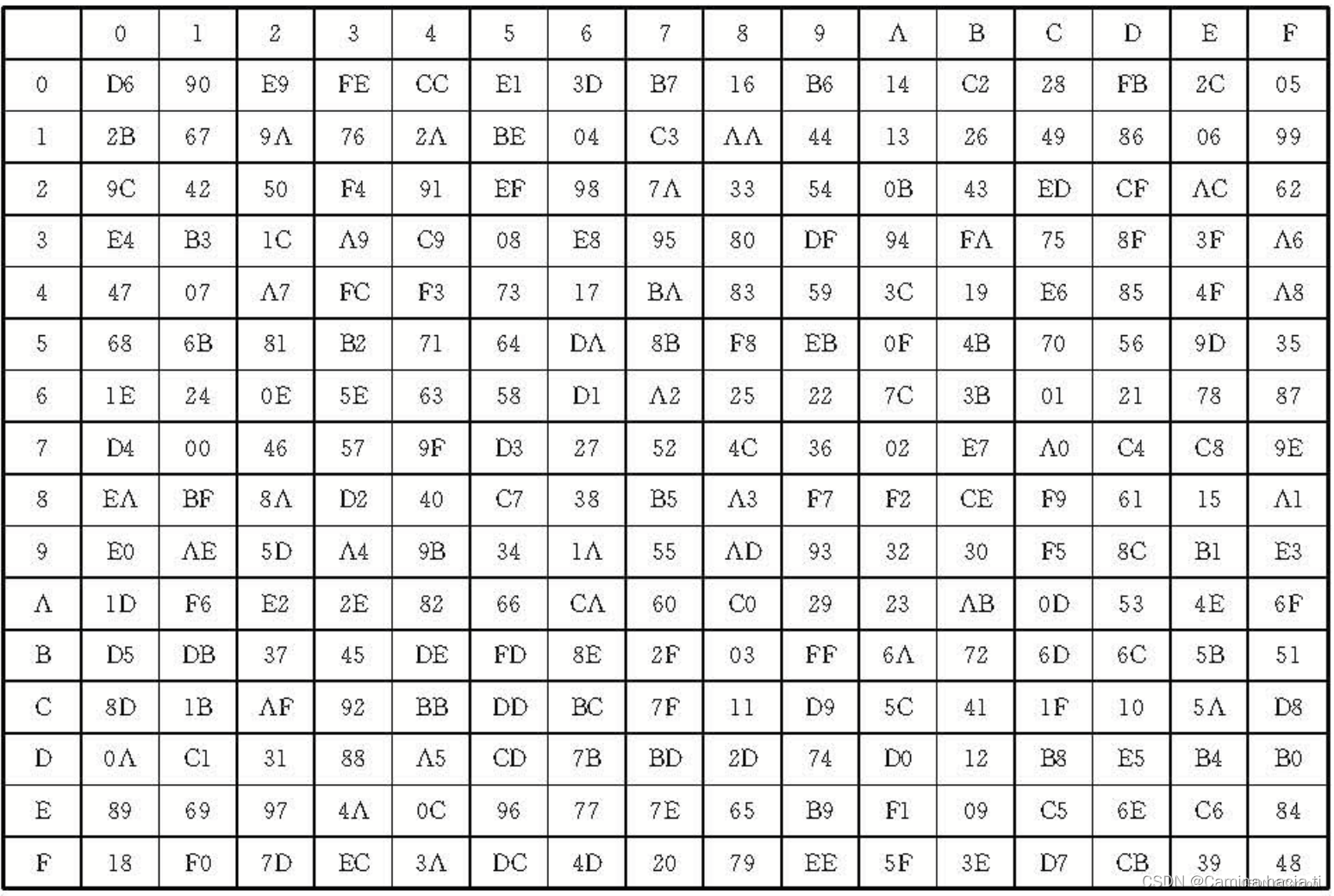
1.3.2S盒

其中数据均为十六进制表示，设其输入为EF，则输出结果是第E行第F列的值，也就是Sbox(EF)=0x84

SM4分组密码算法的ECB模式：
ECB模式的工作方式的运算实例用以验证密码算法的正确性。
ECB

2、算法设计原理

2.1非平衡Feistel网络

平衡网络可以保证可逆性，可以构造高复杂度的f函数，不用在意其可逆性，也不需要实现加密和解密两种不同的算法，Feistel网络可以自动实现。但是现在设计的分组密码要求至少是128Bit，那么分组长度的增加就会导致轮函数f规模的增加。
非平衡Feistel网络将明文分为n个运算字，进行n次迭代就能将明文全部覆盖一遍。