一、题目

给你一个数组 points ，其中 points[i] = [xi, yi] 表示 X-Y 平面上的一个点。求最多有多少个点在同一条直线上。

示例 1：

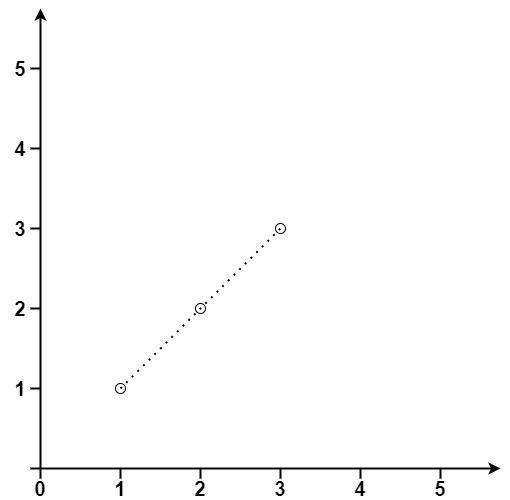
输入：points = [[1,1],[2,2],[3,3]]
输出：3

示例 2：

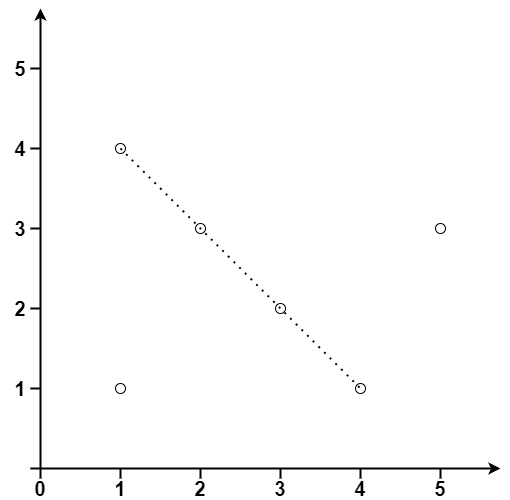
输入：points = [[1,1],[3,2],[5,3],[4,1],[2,3],[1,4]]
输出：4

提示：

1 <= points.length <= 300
points[i].length == 2
-104 <= xi, yi <= 104
points 中的所有点互不相同

二、代码

class Solution {
    public static int maxPoints(int[][] points) {
        int n = points.length;
        int max = 1;
        // 斜率表，单独记录分子和分母
        // key = 3  表示斜率的分子
		// value = {7 , 10}  -> 斜率为3/7的点 有10个
		//         {5,  15}  -> 斜率为3/5的点 有15个
        HashMap<Integer, HashMap<Integer, Integer>> fractionMap = new HashMap<>();
        // 开始从左往右去以(points[i][0], points[i][1])为基础，然后i后面的所有的点与(points[i][0], points[i][1])进行连线，看最多有多少个共线的点
        // 不用判断i之前的位置，因为i之前的位置一定是都判断过了。这里每一轮其他的点都要去连(points[i][0], points[i][1])，因为只有斜率相等且过同一个点才算是共线
        for (int i = 0; i < n - 1; i++) {
            // 记录本轮查询共线的四种情况分别的节点个数
            // 与(points[i][0], points[i][1])在同一个位置的(points[j][0], points[j][1])节点个数
            int cnt1 = 1;
            // 与(points[i][0], points[i][1])的连线在同一竖线的(points[j][0], points[j][1])节点个数
            int cnt2 = 1;
            // 与(points[i][0], points[i][1])的连线在同一横线的(points[j][0], points[j][1])节点个数
            int cnt3 = 1;
            // 与(points[i][0], points[i][1])的连线斜率相等的(points[j][0], points[j][1])节点个数
            int cnt4 = 1;
            // 本轮查询最大的与(points[i][0], points[i][1])共线的节点个数
            int cnt = 0;
            // 斜率分子
            int molecule;
            // 斜率分母
            int denominator;
            // 斜率分子和分母的最小公约数，用于化简斜率分数
            int gcd;
            // 每一轮要清空map，因为斜率相同并不意味着在同一条直线，只有斜率相同，并且过同一个点的两条线才是在同一条直线上。所以到了下一轮之后，所有点共同连线的点就变了，以前的map就都要清空了，因为两轮即使计算出了相同的斜率，因为并不过同一个点，也不是共线的。
            fractionMap.clear();

            // 他俩不用去做化简，在后面与其他点计算得到斜率分数的时候，再去做分数化简即可。
            int x = points[i][0];
            int y = points[i][1];
           
            // 开始将i右边的所有点和(points[i][0], points[i][1])进行连线，判断有多少个是相同点、共横线、共竖线、共斜率的。
            for (int j = i + 1; j < n; j++) {
                // 共点
                if (x == points[j][0] && y == points[j][1]) {
                    cnt1++;
                    // 看共点的数量是否能够超过cnt
                    cnt = Math.max(cnt, cnt1);
                // 共竖线
                } else if (x == points[j][0]) {
                    cnt2++;
                    cnt = Math.max(cnt, cnt2);
                // 共横线
                } else if (y == points[j][1]) {
                    cnt3++;
                    cnt = Math.max(cnt, cnt3);
                // 判断是否是共斜率
                } else {
                    // 计算(points[i][0], points[i][1])和(points[j][0], points[j][1])连线的斜率的分子和分母
                    molecule = x - points[j][0];
                    denominator = y - points[j][1];
                    // 计算分子和分母的最大公约数，将分数进行化简
                    gcd = gcd(molecule, denominator);
                    // 分数化简
                    molecule = molecule / gcd;
                    denominator = denominator / gcd;
                    // 用已经化到最简的斜率分数加入到斜率表fractionMap中，并且得到当前此斜率涉及到的节点个数
                    cnt4 = add(molecule, denominator, fractionMap);
                    // 相同斜率的节点数量是否能够超过cnt
                    cnt = Math.max(cnt, cnt4);

                }
            }
            // 本轮统计完毕，看本轮的个数是否能推高最大值max
            max = Math.max(max, cnt);
        }

        return max;
    }

    // 求a和b的最大公约数：辗转相除法
    public static int gcd(int a, int b) {
        int c = a % b;
        if (c == 0) {
            return b;
        } else {
            return gcd(b, c);
        }
    }

    // 将一个新的斜率x/y加入到斜率表fractionMap中，同时更新这个斜率的直线涉及到的节点数。并且返回这个斜率已有的设计节点的个数
    public static int add(int x, int y, HashMap<Integer, HashMap<Integer, Integer>> fractionMap) {
        // 一定要先判断此时斜率表有没有斜率分子为x的键值对，如果没有，需要先创建一个斜率为x的键值对
        if (!fractionMap.containsKey(x)) {
            HashMap<Integer, Integer> map = new HashMap<>();
            fractionMap.put(x, map);
        }

        // 判断此时有没有分子为x，分母为y的value。注意这里保证一定是有分子为x的value的，因为即使没有上面的操作也已经创建好了
        // 因为可能有很多斜率虽然不同，但是分子是相同的，所以即使不存在x/y的斜率，但是分子为x的可能还会有其他的斜率，所以这里并不能直接创建一个新的HashMap<Integer, Integer>作为x的value，否则会将其他斜率的有效数据给抹掉。
        if (!fractionMap.get(x).containsKey(y)) {
            // 如果此时没有x/y的斜率，就创建一个HashMap<Integer, Integer>，将y加入，并且初始化节点个数为2
            HashMap<Integer, Integer> map = fractionMap.get(x);
            map.put(y, 2);
            fractionMap.put(x, map);
            // 返回x/y这个斜率涉及到的节点个数
            return 2;
        } else {
            // 如果已经有x/y的斜率了，则将这个斜率的节点个数加1
            HashMap<Integer, Integer> map = fractionMap.get(x);
            int cnt = map.get(y);
            map.put(y, cnt + 1);
            fractionMap.put(x, map);
            return cnt + 1;
        }
    }
}