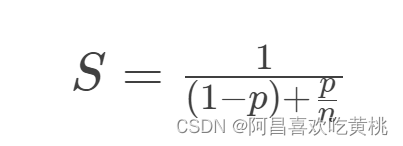点估计
设总体的分布函数形式已知,但它的一个或多个参数为未知,借助于总体的一个样本来估计总体未知参数的值的问题称为点估计问题
矩估计


这个还是看例子会比较好理解一些
例


- 先μ1=E(x),μ2=E(x2)
有几个未知参数就列几次方的期望,但考试应该最多二次(一般情况下,可能考试就只会考这种情况) - 接着,将未知参数用μ1、μ2表示出来
- 然后,μ1和μ2是总体1阶矩和总体2阶矩,替换成样本1阶矩,样本2阶矩(A1,A2)
即直接把未知参数中的μ替换成A,并且未知参数头上再带个破折号。样本1阶矩——样本均值,样本2阶矩 - 样本1阶矩 = (根据图片上的回顾得知)样本偏差
如果题目问得是估计量要将小写字母转成大写字母
概率分布未知时,用矩估计
极大似然估计
理论的知识就不放了,直接看例子会好一些

如果求导(偏导)时,发现找不到最大,就用最大似然原则
离散型——联合分布律、连续型——联合概率密度
例
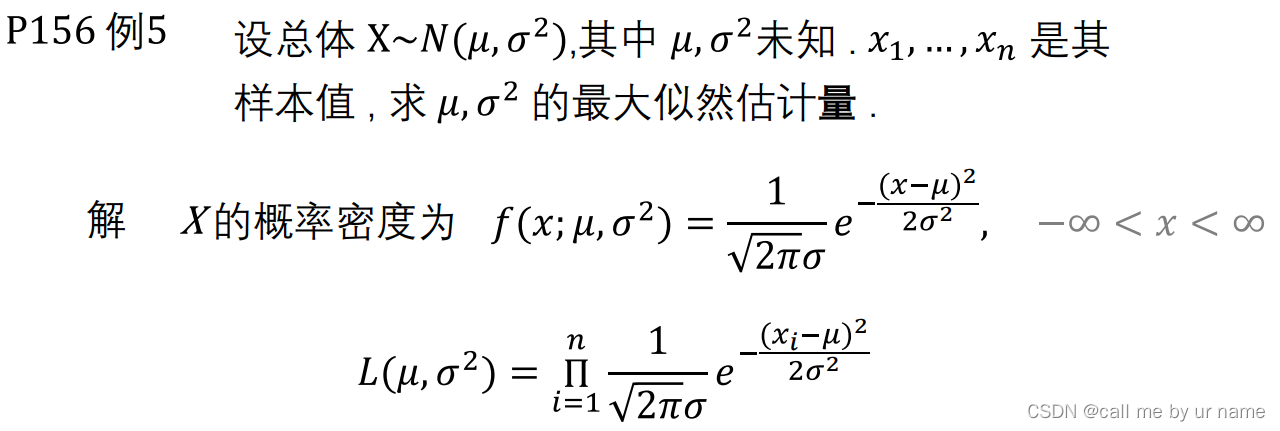


- 先求联合……函数(似然函数)
- 接着对联合函数取对数
- 再对其求导(如果有多个未知参数要求偏导)

这种类型的题就是属于无法求导得到最大值的
就需要用如上这种似然原则推导
如果概率分布已知,就用似然估计
无偏性

不论总体 服从什么分布,只要期望和方差存在:
样本均值是总体均值的无偏估计,样本方差是总体方差的无偏估计。
有效性

相合性

练习
矩估计


这道题主要也是套用上文所学的,只不过这里的期望并不是一眼明了的,需要用到以前的知识计算期望
估计量——大写字母、估计值——小写字母
矩估计——字母上方要带个符号
无序性


要熟悉公式:关于样本平均的方差和均值
离散型似然估计


样本值x1=1,x2=2之类的就是——X1=1,X2=2,所以似然函数那里得到是那样的

![[附源码]JAVA毕业设计医药垃圾分类管理系统(系统+LW)](https://img-blog.csdnimg.cn/dc5b7a96bada4377aa20de907e280e61.png)