题目描述：
给你一个整数 n ，表示有 n 节课，课程编号从 1 到 n 。同时给你一个二维整数数组 relations ，其中 $relations[j]=[prevCoursej,nextCoursej]$，表示课程 $prevCoursej$ 必须在课程 $nextCoursej$ 之前 完成（先修课的关系）。同时给你一个下标从 0 开始的整数数组 $time$ ，其中 $time[i]$ 表示完成第 (i+1) 门课程需要花费的 月份 数。

请你根据以下规则算出完成所有课程所需要的 最少 月份数：

如果一门课的所有先修课都已经完成，你可以在 任意 时间开始这门课程。
你可以 同时 上 任意门课程 。
请你返回完成所有课程所需要的 最少 月份数。

注意：测试数据保证一定可以完成所有课程（也就是先修课的关系构成一个有向无环图）。

示例 1:

输入: n = 6, edges = [[0,1],[0,2],[2,3],[2,4],[2,5]]
输出: [8,12,6,10,10,10]
解释: 树如图所示。
我们可以计算出 dist(0,1) + dist(0,2) + dist(0,3) + dist(0,4) + dist(0,5) 
也就是 1 + 1 + 2 + 2 + 2 = 8。 因此，answer[0] = 8，以此类推。

示例 2：

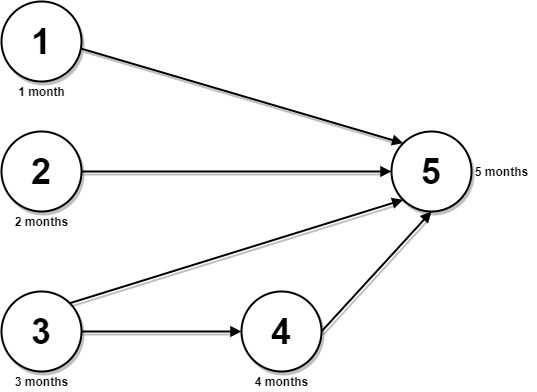
输入：n = 5, relations = [[1,5],[2,5],[3,5],[3,4],[4,5]], time = [1,2,3,4,5]
输出：12
解释：上图展示了输入数据所表示的先修关系图，以及完成每门课程需要花费的时间。
你可以在月份 0 同时开始课程 1 ，2 和 3 。
在月份 1，2 和 3 分别完成这三门课程。
课程 4 需在课程 3 之后开始，也就是 3 个月后。课程 4 在 3 + 4 = 7 月完成。
课程 5 需在课程 1，2，3 和 4 之后开始，也就是在 max(1,2,3,7) = 7 月开始。
所以完成所有课程所需的最少时间为 7 + 5 = 12 个月。

解题思路：

这个题其实类似于我们算数据结构中AOE图的起点到终点的最少权值。
在建完图之后， 按拓扑排序的顺序更新达每节课的最早完成时间
我们让 $reach[i]$ 表示完成第 $i$ 门课程的最短时间，然后若结点u和v之间有边，则v的最早完成时间就是v的所有现行课程同时进行的最早完成时间加上v的课程时间，于是则有：$reach[v]=max(reach[u]+time[v-1],reach[v]);$。
拓补排序结束之后，reach中的最大值即为所求的答案。

AC代码如下：

class Solution {
public:
    static const int maxn = 5e4+5;
    int minimumTime(int n, vector<vector<int>>& relations, vector<int>& time) {
        vector<int>G[n+2];
        queue<int>q;
        vector<int>reach(n + 2, 0);
        int indegree[maxn] = {0}, ans = 0;
        for(auto relation : relations) { // 建图
            G[relation[0]].push_back(relation[1]);
            indegree[relation[1]] ++; // 入度加一
        }
        for(int i = 1; i <= n; i++) {
            if(indegree[i] == 0) {
                reach[i] = time[i-1];
                q.push(i);
            }
        }
        while(!q.empty()) { // 拓补排序
            int u = q.front();
            q.pop();
            for(int i = 0; i < G[u].size(); i++) {
                int v = G[u][i];
                reach[v] = max(reach[u] + time[v - 1], reach[v]);
                indegree[v]--;
                if(indegree[v] == 0) q.push(v);
            }
        }
        for(auto i : reach) ans = max(ans, i);
        return ans;
    }
};