Problem - 7321

题目大意：在(n+2)*(m+2)的棋盘上，中间摆满了n*m个棋子，每个棋子可以向上下左右四个方向移动，对于相邻的三格，移动前后分别为 有 有 无->无 无 有，问最后棋盘上最少能剩下几个棋子

1<=n,m<=65

思路：我们首先要将棋盘从复杂变简单，也就是要在棋盘基本形状不变的情况下，缩减它的行列数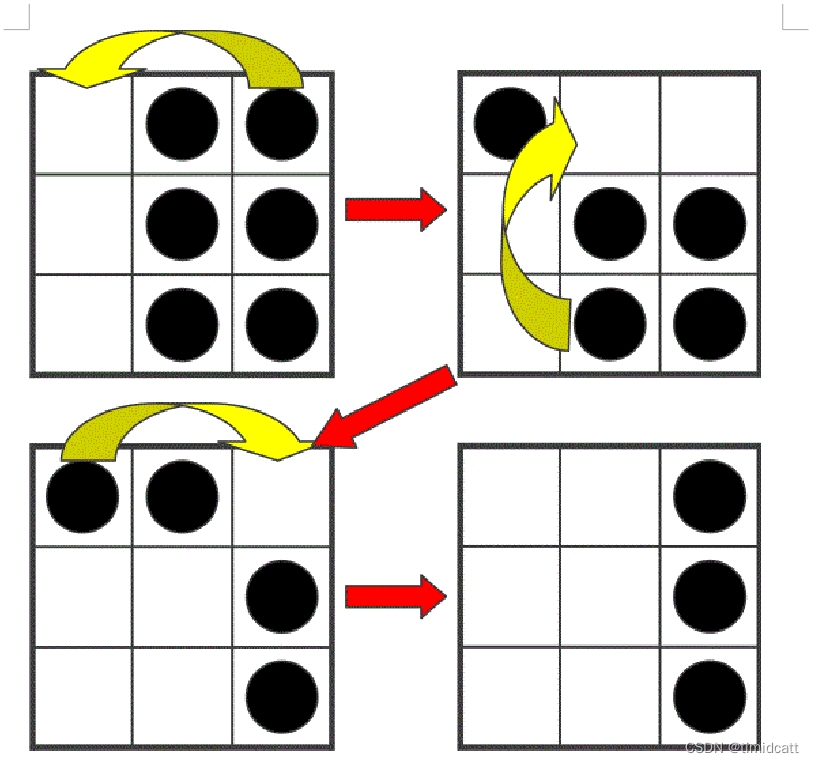

从上图中可以发现，我们可以将一个3*2的棋盘利用左边一列的空间，将其缩减为3*1的，扩展来说，任意3*n的棋盘，n都可以被减小到我们想要的数，但只有3还不够，我们还需要研究2*n的棋盘如何缩减，因为2x+3y才可以等于任意整数

 

从上图可以发现，对于一个2*4的棋盘，我们可以借助上面一行，将其缩减为2*1，因此对于任意n>=4，我们都可以将2*n的棋盘缩减成2*我们想要的数。然后又可知，当棋盘只有一行或一列时，棋子只能剩下n*m/2个，这是很大的情况，我们不想要，所以我们要尽量把棋盘缩减到2*2，所以我们先将n,m>=5的部分，一直-3，直到<5，然后继续讨论剩下的情况当n=4,m=4时，此时比较特殊，我们有方法可以把棋子减到1个：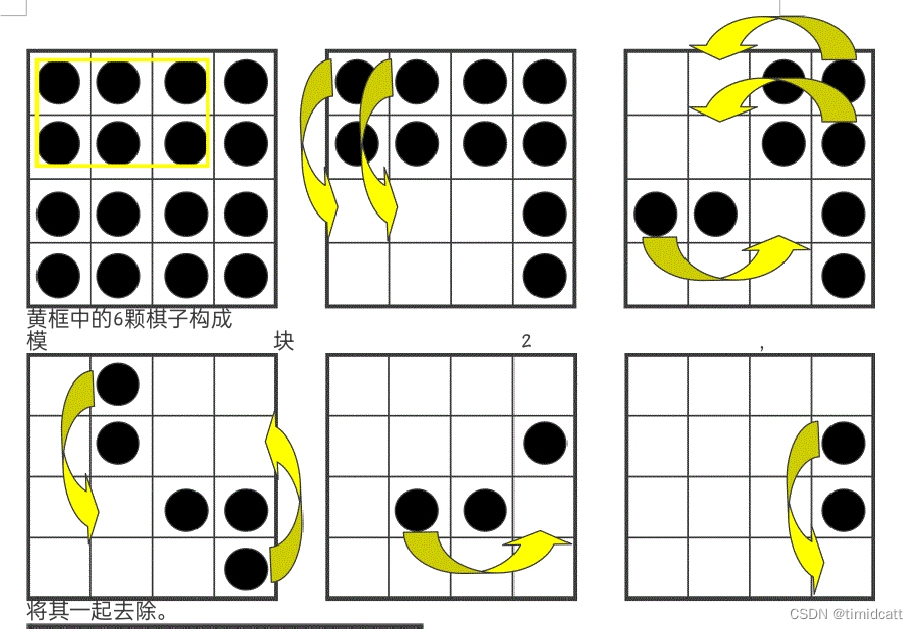

令n>=m，n=4,m=3时，我们可以将它缩减成2*3，然后只能剩下2个，n=4,m=2，我们将它缩减成1*2，剩下1个,n=3,m=3/2，和4*3同理，n=2,m=2时，可以只剩下一个，所有情况就都讨论完毕了

#include<__msvc_all_public_headers.hpp>
//#include<bits/stdc++.h>
using namespace std;
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	int t;
	cin >> t;
	while (t--)
	{
		int n, m;
		cin >> n >> m;
		if (n < m)
			swap(n, m);	
		if (m == 1)
		{
			cout << (n - 1) / 2 + 1 << endl;
			continue;
		}
		while (n >= 5)
		{
			n -= 3;
		}
		while (m >= 5)
		{
			m -= 3;
		}			
		if (n < m)
			swap(n, m);
		if (n == 4 && m == 4)
		{
			cout << 1 << endl;
		}
		else if (n == 4 && m == 3)
		{
			cout << 2 << endl;
		}
		else if (n == 4 && m == 2)
		{
			cout << 1 << endl;
		}
		else if (n == 3 && m == 3)
		{
			cout << 2 << endl;
		}
		else if (n == 3 && m == 2)
		{
			cout << 2 << endl;
		}
		else if (n == 2 && m == 2)
		{
			cout << 1 << endl;
		}
	}
}