编程的方法往往不止一种，比如怎么把一个Python种的列表拆成N个子列表，我们可以很容易找到N种方法，也许这就是编程的魅力所在。

一、列表表达式法

这种方法最为简洁，不过可读性差一些

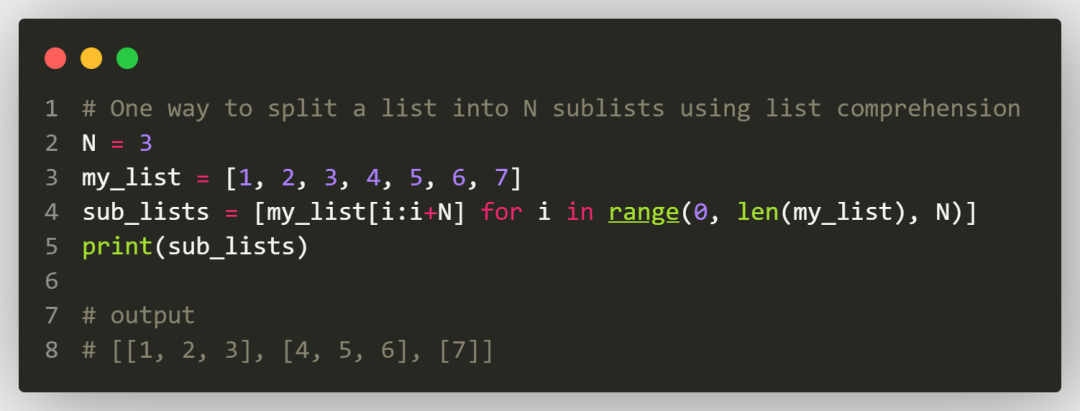
    这个方法中，即使原始列表的数量无法被N整除，也不会出错，其实那是因为使用列表的切片功能访问列表时，只要切片中首位不越界，末位无所谓，这是python的一大亮点。但是看上例来说，如果我们足够吹毛求疵，会发现它还有点不完美。拆分后的子列表，第一个和第二个子列表的长度都为3，最后一个子列表只有一个元素了，拆分不够均匀。

    要是有一种算法能实现，当列表长度无法被N整除时，每个列表的长度都均匀少一点，每个子列表的总长度都相差不超过1，该有多好啊？这就要提到我们的方法二了。

二、利用贪心算法

　　永远往最短子列表中添加元素法

　　先构造一个列表，内部构造N个子空列表：[[],[],[],[]] .遍历原始列表的每个元素，当把这个元素往结果列表的哪个子列表中追加时，永远用min方法看哪个子列表的长度最短，谁的长度最短，说明给它append的子元素最少，我们就优先给它插入新元素，思路很巧妙，代码如下：

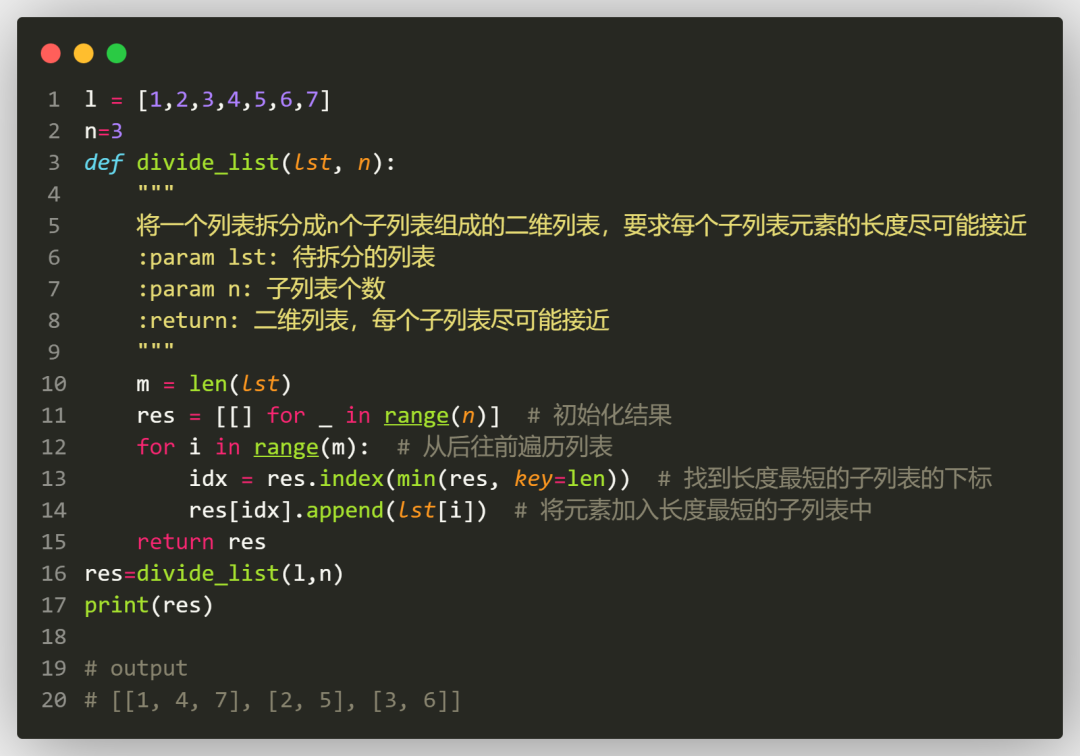
     但是仔细一看，这个方法还是有缺点，idx = res.index(min(res, key=len))  这句（找到长度最短的子列表的下标）方法很浪费性能，也许我们不用每次都用min方法逐个判断子列表长度来确定待追加元素的子列表。

三、发扑克牌法

    一开始每个子列表的元素本就为空，我们永远依次给每个子列表追加元素，一轮接着一轮，这样大家的长度就应该接近。就像发扑克牌一样的道理。算法上应该是这样写：

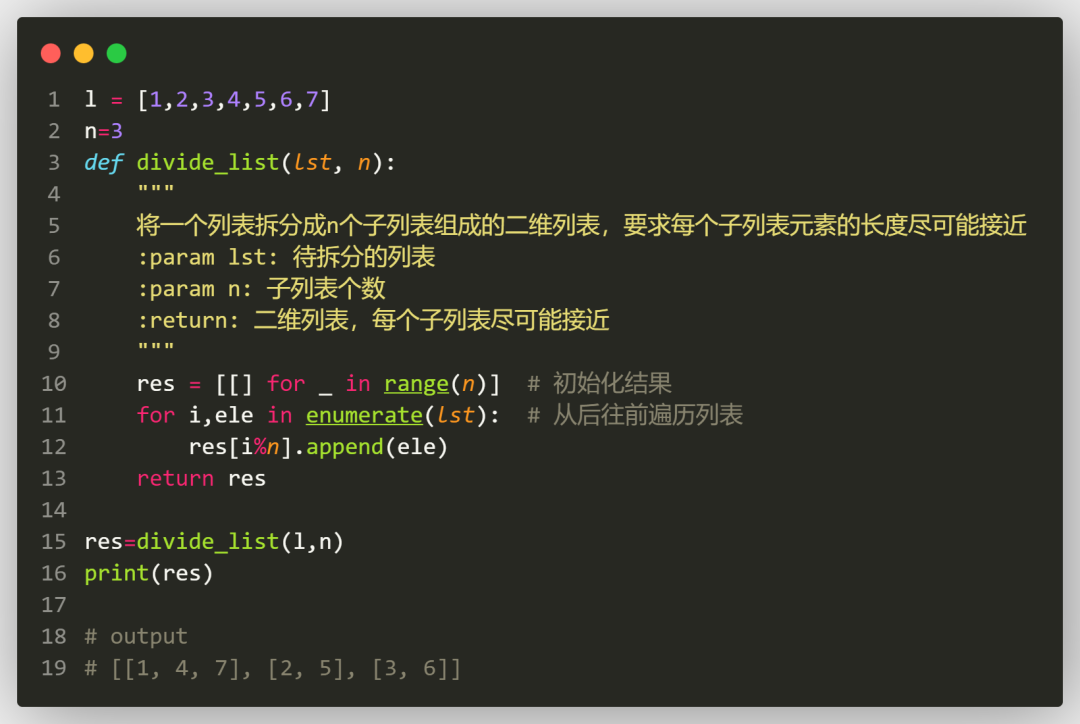
    作为完美主义者来讲，这样拆分列表依然有瑕疵。原始的列表为l = [1,2,3,4,5,6,7]，拆分后的output=[[1, 4, 7], [2, 5], [3, 6]]，怎么感觉两者长得不像呢？

    有没有一种拆分列表的算法，可以把方法一的【保留列表元素顺序】和方法三【子列表数量相差不超过1】 这两者的优点有效结合呢？

必须有啊。

四、动态确定长度+列表切片

    我们只需要在发牌前，先计算出每个子列表的理论长度，再从原始列表中根据切片拿到特定长度的元素给到每个子列表，不就大功告成了

。有了思路，代码那叫一个Easy。

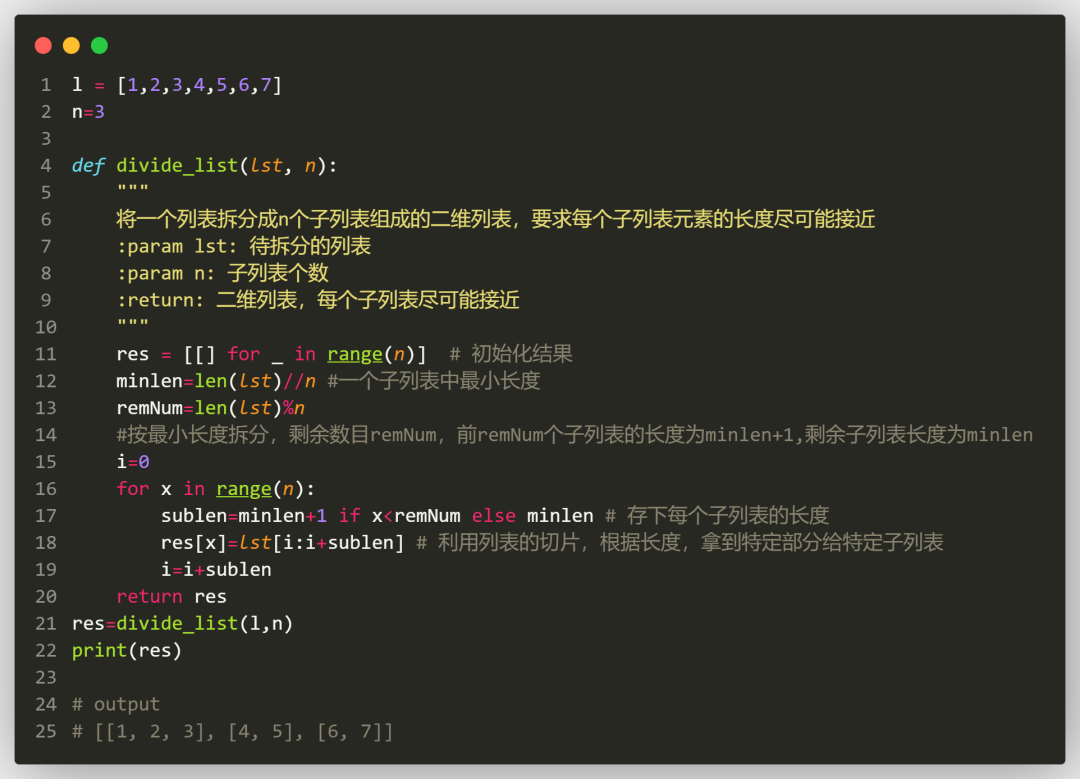
方法四，如果我们进一步用列表表达式来优化，还可以更简洁，比如就像这样：

 

    过分的简洁有时候也会导致更差的可读性。屏幕前的你，更接受用上面哪种方法来拆分列表呢？