基础数据结构

1.基础概念

数据结构是一种具有一定逻辑关系，在计算机中应用某种存储结构，并且封装了相应操作的数据元素的集合。它包含三方面的内容，逻辑关系、存储关系以及操作。

一般而言，数据结构的选择首先会从抽象数据类型的选择开始。一个设计良好的数据结构，应该在尽可能使用较少的时间与空间资源的前提下，为各种临界状态下的运行提供支持。数据结构可通过编程语言所提供的数据类型、引用及其他操作加以实现。

不同种类的数据结构适合于不同种类的应用，而部分甚至专门用于特定的作业任务。例如，当计算机网络依赖于路由表运作时，B树高度适用于数据库的封装。

在许多类型的程序设计中，选择适当的数据结构是一个主要的考虑因素。许多大型系统的构造经验表明，封装的困难程度与最终成果的质量与表现，都取决于是否选择了最优的数据结构。在许多时候，确定了数据结构后便能很容易地得到算法。而有些时候，思路则会颠倒过来：例如当某个关键作业需要特定数据结构下的算法时，会反过来确定其所使用的数据结构。然而，不管是哪种情况，数据结构的选择都是至关重要的。

系统构造的关键因素是数据结构而非算法的这一深入理解，导致了多种形式化的设计方法与编程语言的出现。绝大多数的语言都带有某种程度上的模块化思想，通过将数据结构的具体实现封装隐藏于受限接口之后的方法，来让不同的应用程序能够安全地重用这些数据结构。C++、Java、Python等面向对象的编程语言可使用类来完成这一功能。

因为数据结构的重要性毋庸置疑，现代编程语言及其运行环境在标准库中都包含了多种数据结构，例如C++标准模板库中的容器、Java集合框架以及微软的.NETFramework。

大多数数据结构都由数列、记录、可辨识联合、引用等基本类型构成。举例而言，可空引用（nullablereference，一种可被置空的引用）是引用与可辨识联合的结合体，而最简单的链式结构链表则是由记录与可空引用构成。

数据结构意味着接口或封装：一个数据结构可被视为两个函数之间的接口，或者是由数据类型联合组成的存储内容的访问方法封装。

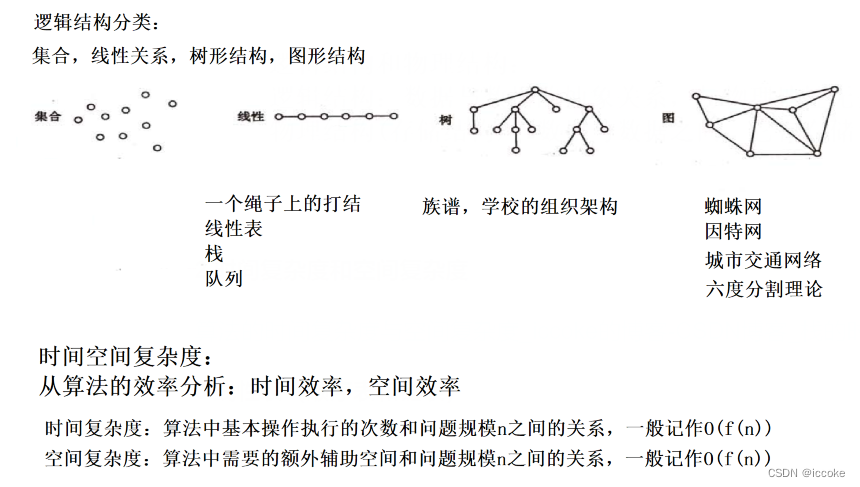
2.时间复杂度和空间复杂度

算法的时间复杂度与空间复杂度_iccoke的博客-CSDN博客_栈的时间复杂度和空间复杂度

3.线性表（顺序表和链表）

实际上线性表中的顺序表可以看作一个特殊的数组存储模式

我们可以在不同位置进行插入和删除操作，然后根据有效格子数和总长度对顺序表实行变更

这是《大话数据结构中关于顺序表的实列》

着就阐述了顺序表在储存数据时的便利

可以在不同的场景下进行变更，从而达到可以适应多种场景的情况

这是关于顺序表的存储模式的结构体的定义

有效长度改变就可以达到删除和插入的功能

而总的空间大小可以实现扩容等操作

实际上顺序表的存储模式和一维数组的存储模式是类似的

我们在插入删除时仍可以使用一维数组插入删除时的思路

我们通过宏定义来实现有效空间大小的

接下来我们就来实现一个顺序表

这里因为结构和一维数组类似

我们只实现部分内容

首先时顺序表的初始化

我们可以要对他的结构体中的每一项都进行初始化

用malloc申请内存来初始化我们的格子

void Init_Sqlist(struct Sqlist* sq)
{
	sq->elem = (ELEM_TYPE *)malloc(LIST_INIT_SIZE * sizeof(int));
	assert(sq->elem != NULL);
	sq->length = 0;
	sq->listsize = LIST_INIT_SIZE;
}

其次是插入和删除

因为顺序表是有格子数和大小

因此我们需要在插入之前判断是否满

满的话进行插入失败或者扩容操作

要在删除是判空操作

bool Del_head(struct Sqlist* sq)
{
	//1插入需要判满 删除也需要判空
	if(IsEmpty(sq))
	{
		return false;
	}
	//上面if没成功，则代表有数据

	//2.待删除元素，后面的元素向前覆盖
	for(int i=1; i<sq->length; i++)
	{
		sq->elem[i-1] = sq->elem[i];
	}

	//3.有效长度-1
	sq->length--;

	return true;
}

这是头删内容

其余和这个类似

删除时将待删除位置删掉，然后后面的数据依次往前挪动

插入时依次往后挪动

这都是一般情况

我们在尾删时可以直接改变有效个数达到不进行删除操作的删除

最后让我们看看顺序表的优缺点