一、本周周赛总结

• 4发苍蝇呵呵呵呵呵。
• T1暴力。
• T2dp。
• T3暴力。
• T4离线+堆BFS。
• 

二、 [Easy] 6257. 删除每行中的最大值

链接: 6257. 删除每行中的最大值

1. 题目描述

2. 思路分析

• 比赛时非常麻烦的模拟了，把每个数冒泡出来删除。
• 实际上对每行排序，然后取每列最大即可。
• py可以用*展开grid然后zip起来就获得每列。

3. 代码实现

class Solution:
    def deleteGreatestValue(self, g: List[List[int]]) -> int:        
        ans = 0
        for r in g:
            r.sort()
        return sum(max(col) for col in zip(*g))            

三、[Medium] 6258. 数组中最长的方波

链接: 6258. 数组中最长的方波

1. 题目描述

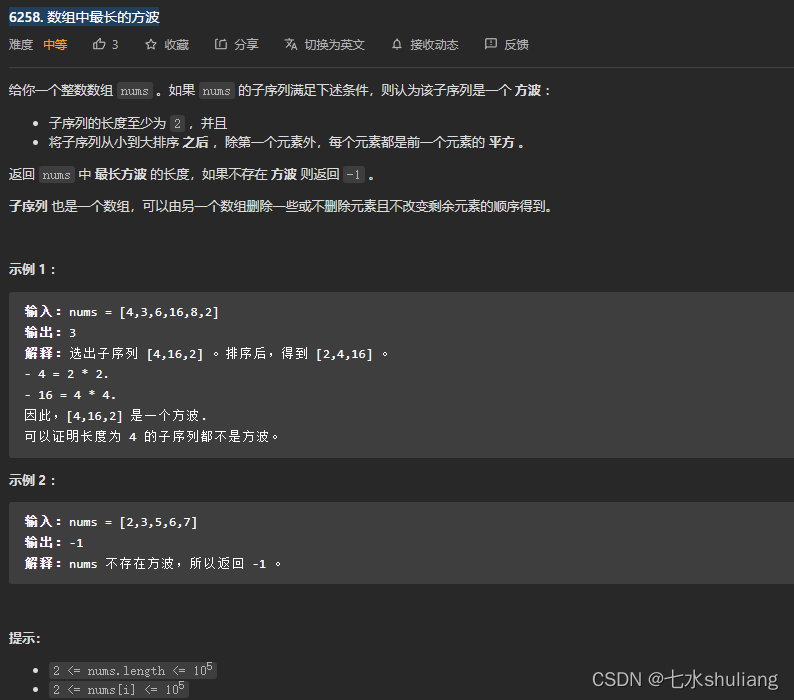
2. 思路分析

用哈希表存dp。

• 令f[i]为以i为结尾的方波长度（认可长度1）。
• 显然f[i] = f[sqrt(i)]+1。
• 涉及浮点运算不知道稳不稳，反正过了。
• 忽略开方开销的话，复杂度是log(U),
• 如果复杂度不想和数值上限相关，需要排序。

---

• dp相当于枚举终点，枚举起点的话，可以直接暴力，因为上限会很快增长到溢出。

3. 代码实现

class Solution:
    def longestSquareStreak(self, nums: List[int]) -> int:       
        f = {x:1 for x in nums}
        for i in range(4,max(nums)+1):
            if i in f:
                x = int(i**0.5)
                if x*x == i and x in f:
                    f[i] = f[x] + 1
        ans = max(f.values())
        return ans if ans>=2 else -1     

四、[Medium] 6259. 设计内存分配器

链接: 6259. 设计内存分配器

1. 题目描述

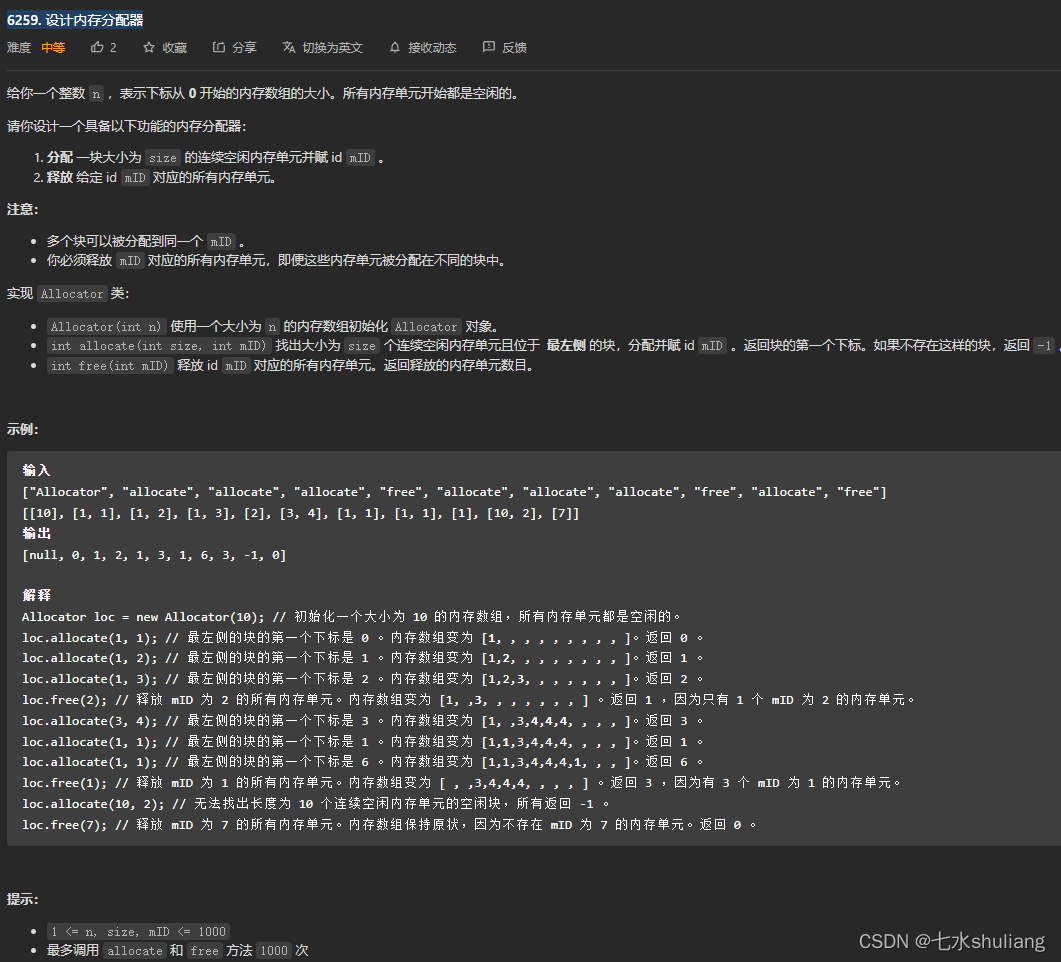
2. 思路分析

• 看了下复杂度，直接暴力。

3. 代码实现

class Allocator:

    def __init__(self, n: int):
        self.a = [0]*n

    def allocate(self, size: int, mID: int) -> int:
        cnt = 0
        for i ,v in enumerate(self.a):
            if v:
                cnt = 0
            else:
                cnt += 1
                if cnt == size:
                    self.a[i-cnt+1:i+1] = [mID]*cnt
                    return i-cnt+1
        return -1

    def free(self, mID: int) -> int:
        ans = 0
        for i,v in enumerate(self.a):
            if v == mID:
                self.a[i] = 0
                ans += 1
        return ans

五、[Hard] 6260. 矩阵查询可获得的最大分数

链接: 6260. 矩阵查询可获得的最大分数

1. 题目描述

2. 思路分析

• 读完题直接贴了个并查集板子，然后没用到：并查集要把点权转化为边权很麻烦。

---

离线+堆bfs。

• 题目的询问query实际上limit，即询问：对于limit从左上角开始，能floodfill到的格子个数。
• 再转换一下：左上角从虚空连接了高度limit的海平面，问能淹几个格子。
• 那么把询问离线排序，从小到大处理即可。
• 队列用小顶堆存，含义为：边界的格子最矮值先被淹。
• 于是只有堆顶小于limit时才需要继续搜索；否则等待海平面上升。

3. 代码实现

DIRS = ((0,1),(0,-1),(1,0),(-1,0))
class Solution:
    def maxPoints(self, g: List[List[int]], q: List[int]) -> List[int]:
        m,n,k = len(g),len(g[0]),len(q)
        ans = [0]*k
        q = sorted((v,i) for i,v in zip(range(k),q))
        def inbound(x,y):
            return 0<=x<m and 0<=y<n        
        pq = [(g[0][0],0,0)]
        g[0][0] = 0
        cur = 0
        for v,i in q:            
            while pq and pq[0][0]<v:
                cur += 1
                _,x,y = heappop(pq)
                for dx,dy in DIRS:
                    a, b = x+dx, y+dy
                    if inbound(a,b) and g[a][b]:             
                        heappush(pq,(g[a][b],a,b))                                              
                        g[a][b] = 0                   
           
            ans[i] = cur
        return ans

六、参考链接