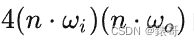给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 

class Solution {
    public int trap(int[] height) {
        int len =  height.length;
        int ans = 0; //结果

        int i;
        //左侧雨水
        //去除开头为0
        for(i = 0;i<len && height[i]==0;i++);

        int j = i++;//左侧第一个不为0的下标
        
        for(;i<len;i++){
            //记录 [2 0 2]    这种所有要写 >= 记录下来雨水
            if(height[i] >= height[j]){
                //统计 i 跟 j 之间有多少雨水
                for(int k = j+1;k<i;k++){
                    ans += height[j] - height[k];
                }
                //设置j的新起点
                j = i;
            }   
        }

        //为什么记录右侧雨水不怕中间重复呢，因为从左开始记录雨水就只有height[i] >= height[j]才会记录
        //而记录右侧雨水时只有height[i] > height[j]才会记录，其实记录雨水时，ans最多发生一次改变
        //就是[3 2 1 2 1]这种情况就要记录右侧雨水
        //           |
        //  |     |  |  |     |  
        //  |  |  |  |  |  |  |  |
        //  0  1  2  3  4  5  6  7
        //从左侧记录时雨水为1,其实下标为5地方也能存个一雨水，所有才要再从右侧执行一次

        //右侧雨水    
        //去除结尾为0
        for(i = len-1;i>=0 && height[i]==0;i--);
        j = i--;//右侧第一个不为0的下标
        
        for(;i>=0;i--){
            //这里就写 > 就行了，因为上面已经记录了
            if(height[i] > height[j]){
                //统计 i 跟 j 之间有多少雨水
                for(int k = j-1;k>i;k--){
                    ans += height[j] - height[k];
                }
                //设置j的新起点
                j = i;
            }   
        }
        return ans;
    }
}

思路二：

class Solution {
    //                 h: 0 1 0 2 1 0 1 3 2 1 2 1
    //前缀最大值数组 pre: 0 1 1 2 2 2 2 3 3 3 3 3
    //后缀最大值数组 suf: 3 3 3 3 3 3 3 3 2 2 2 1
    //算法核心  ans += Math.min(pre[i],suf[i]) - h[i];
    //取最小边的高度 - 自己的高度
    
    //下面是优化而来
    public int trap(int[] height) {
        int ans = 0;
        int len = height.length;
        int pre_max=0, suf_max=0;//前缀最大值和后缀最大值
        int l = 0,r=len-1;
        while(l<r){
            pre_max = Math.max(pre_max,height[l]);
            suf_max = Math.max(suf_max,height[r]);
            if(pre_max < suf_max){
                ans += pre_max - height[l++];
            }else{
                ans += suf_max - height[r--];
            }
        }
        return ans;
    }
}