实验任务

(1) 掌握顺序查找算法的实现；
(2) 掌握二分查找算法的实现；
(3) 掌握两种查找算法的时间复杂度与适用场合。

实验内容

(1) 基于顺序查找表实现顺序查找和二分查找算法；
(2) 使用两个不同大小的查找表进行两次理论和实际性能对比；
(3) 根据实验环境调整两次查找表的大小，使得：
      i.第1次查找表的长度 = ⌊ 第2次查找表长度 / 10 ⌋；
      ii.第2次顺序查找的时间介于 [ 9000, 9999 ] ms之间。
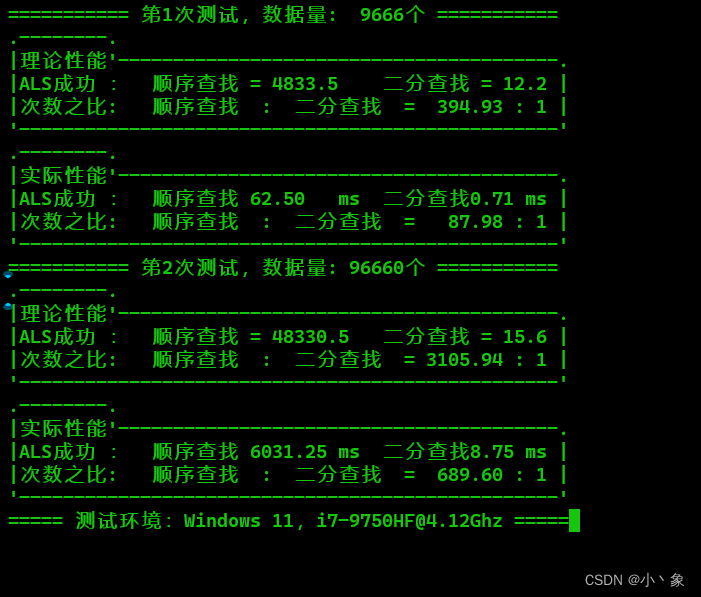
(4) 输出实验结果，结果应与如下图1所示尽可能相似。

实验源码

注意：由于编译器优化或电脑编程环境缓存等因素，实际运行和理论值可能有差距

//
// Created by Lenovo on 2022-05-27-上午 9:14.
// 作者：小象
// 版本：1.0
//

#include <malloc.h>
#include <stdio.h>
#include <math.h>
#include <pthread_time.h>
#include <profileapi.h>

#define MAXSIZE 2147483 // int型0~21亿 顺序表可能达到的最大长度10位
#define OK 1
#define ERROR 0

// 数据元素类型定义
typedef struct {
    int key; // 关键字域
    int otherInfo; // 其他域
} ElemType;

// 顺序表定义
typedef struct {
    ElemType *elem; // 存储空间的基地址
    int length; // 当前长度
} SqSTable;

int InitTable(SqSTable *table); // 顺序表的初始化
int CreateTable(SqSTable *table, int length); // 顺序表的创建
double SearchSeq(SqSTable table, int key); // 顺序查找
double SearchSeq_Times(SqSTable table); // 顺序查找完 key 个关键字耗时
double SearchBin(SqSTable table, int key); // 二分查找
double SearchBin_Times(SqSTable table); // 二分查找完 key 个关键字耗时
void PrintResult(int data, double sequentialTimes, double binaryTimes); // 打印最终结果

/**
 * <h2>二分查找 和 顺序查找算法 实验一</h2>
 * <h3>实验要求：</h3>
 * i.第1次查找表的长度 = 第2次查找表长度 / 10； <br>
 * ii.第2次顺序查找的时间介于 [ 9000, 9999 ] ms之间。 <br>
 * @return 0
 */
int main() {

    SqSTable table;
    if (!(InitTable(&table))) {
        printf("空间申请失败！！！");
    }
    // 两种查找方式的所查找的数据量
    int test_01_data = 9666;
    int test_02_data = test_01_data * 10;
    /*
     * 第一次测试
     */
    printf("=========== 第1次测试，数据量:%6d个 ===========\n", test_01_data);
    // 创建顺序表
    CreateTable(&table, test_01_data);
    // 顺序查找
    double sequentialTimes_01 = SearchSeq_Times(table);
    // 二分查找
    double binaryTimes_01 = SearchBin_Times(table);
    // 查找结果
    PrintResult(test_01_data, sequentialTimes_01, binaryTimes_01);


    /*
     * 第二次测试
     */
    printf("=========== 第2次测试，数据量:%6d个 ===========\n", test_02_data);
    // 创建顺序表
    CreateTable(&table, test_02_data);
    // 顺序查找
    double sequentialTimes_02 = SearchSeq_Times(table);
    // 二分查找
    double binaryTimes_02 = SearchBin_Times(table);
    // 查找结果
    PrintResult(test_02_data, sequentialTimes_02, binaryTimes_02);

    // 测试环境
    printf("===== 测试环境：Windows 11，i7-9750HF@4.12Ghz =====");

    getchar();
}

// 构造一个空的顺序表
int InitTable(SqSTable *table) {
    table->elem = (ElemType *) malloc(sizeof(SqSTable) * MAXSIZE); // 动态方式需要先分配内存，而且
    // 需要用到malloc函数申请，有可能申请不到，申请到后malloc()函数会把申请到的连续数据空间首地址返回
    // 注意：这里申请到返回的地址是十六进制的地址，而elem只能存十进制的地址，所以需要强转为十进制地址后赋值
    if (table->elem == NULL) { // 如果没有申请到地址，退出
        return ERROR;
    }
    table->length = 0; // 空表长度为 0
    return OK; // 初始化成功
}

// 顺序表的创建
int CreateTable(SqSTable *table, int length) {
    for (int i = 1; i <= length; i++) { // 第一个数默认不使用
        table->elem[i].key = i;
        table->length++; // 表长加 1
    }
    return OK;
}

// 顺序查找
double SearchSeq(SqSTable table, int key) {
    int i;
    table.elem[0].key = key; // 第一个数的作用来了 -> 设置 “哨兵”
    for (i = table.length; table.elem[i].key != key; i--); // 从后往前找
}

// 顺序查找测时
double SearchSeq_Times(SqSTable table) {
    /*
     * 时间测试方式二：
     *      所用精度：纳秒级
     */
    struct timespec start;
    struct timespec end;
    // 开始时间
    clock_gettime(CLOCK_PROCESS_CPUTIME_ID, &start);

    for (int i = 1; i <= table.length; i++) { // 所有数都查找一遍
        SearchSeq(table, i);
    }

    // 结束时间
    clock_gettime(CLOCK_PROCESS_CPUTIME_ID, &end);
    // 总耗时
    // 转化为 ms 为单位（但是精度可以直接到 ns 级别）
    double start_ms = start.tv_sec * 1000.0 + start.tv_nsec / 1000000.0;
    double end_ms = end.tv_sec * 1000.0 + end.tv_nsec / 1000000.0;
    return end_ms - start_ms;
}

// 在有序表table中折半查找其关键字等于key的数据元素。若找到，则函数值为该元素在表中的位置，否则为0
double SearchBin(SqSTable table, int key) {
    // 置 查找区间 初值
    int leftIndex = 1; // 第一个数默认不使用
    int rightIndex = table.length;
    while (leftIndex <= rightIndex) { // 循环限制条件：查找过程中如果没有找到的情况，会造成栈溢出
        int minIndex = (leftIndex + rightIndex) / 2; // 二分查找的精髓：先找到中间那个数
        if (key == table.elem[minIndex].key) {
            // 如果需要查找的数等于中间那个数，则直接输出中间那个数(即需要查找的数的)下标
            return minIndex; // 找到待查元素
        } else if (key < table.elem[minIndex].key) {
            // 如果需要查找的数小于中间那个数，说明需要从中间那个数的左边第一个数继续进行二分查找，其他不变
            rightIndex = minIndex - 1;
        } else {
            // 如果需要查找的数大于中间那个数，说明需要从中间那个数的右边第一个数继续进行二分查找，其他不变
            leftIndex = minIndex + 1;
        }
    }
    return -1; // 如果没有找到返回-1
}

// 二分查找测时
double SearchBin_Times(SqSTable table) {
    /*
     * 时间测试方式二：
     *      所用精度：微秒级
     */
    union _LARGE_INTEGER time_start; // 开始时间
    union _LARGE_INTEGER time_over; // 结束时间
    LARGE_INTEGER f; // 计时器频率
    QueryPerformanceFrequency(&f);
    double dqFreq = (double) f.QuadPart; // 计时器频率
    QueryPerformanceCounter(&time_start); // 计时开始

    for (int i = 1; i <= table.length; i++) { // 所有数都查找一遍
        SearchBin(table, i);
    }

    QueryPerformanceCounter(&time_over); // 计时结束
    // 乘以1000000把单位由秒化为微秒，精度为1000 000/（cpu主频）微秒
    double run_time = 1000000.0 * (time_over.QuadPart - time_start.QuadPart) / dqFreq;
    return run_time / 1000.0;
}

void PrintResult(int data, double sequentialTimes, double binaryTimes) {

    // 理论ASL
    double sequentialASL = (data + 1) / 2.0;
    double binaryASL = log2(data + 1) - 1;

    printf(".--------.\n");
    printf("|理论性能'----------------------------------------.\n");
    printf("|ALS成功 ：　顺序查找 = %-7.1f   二分查找 = %-4.1f |\n", sequentialASL, binaryASL);
    printf("|次数之比:   顺序查找  :  二分查找  = %7.2f : 1 |\n", sequentialASL / binaryASL);
    printf("'-------------------------------------------------'\n");

    printf(".--------.\n");
    printf("|实际性能'----------------------------------------.\n");
    printf("|ALS成功 ：　顺序查找 %-7.2f ms  二分查找%-4.2f ms |\n", sequentialTimes, binaryTimes);
    printf("|次数之比:   顺序查找  :  二分查找  = %7.2f : 1 |\n", sequentialTimes / binaryTimes);
    printf("'-------------------------------------------------'\n");

}

实验结果