👨‍🎓个人主页：研学社的博客 

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🌈3 Matlab代码实现

🎉4 参考文献

---

💥1 概述

本文是一个元胞自动机模型，模拟由于不应期弥散机制引起的心房扑动/颤动。

（4）个细胞簇被快速刺激，导致周期性的激活波
在整个模型表面上传播。由于整个表面不应期的变化，波前在与仍然耐火的区域碰撞时被分解。快速刺激在80步后终止，但激活波前仍然在整个模型表面传播。作者通过寻找不应期短的相邻细胞来仔细选择刺激的细胞簇。我在这里不这样做;我在这里不这样做。相反，我只是不断改变用于分配 K 值的随机数生成器的初始状态，直到我获得自我维持的活动。

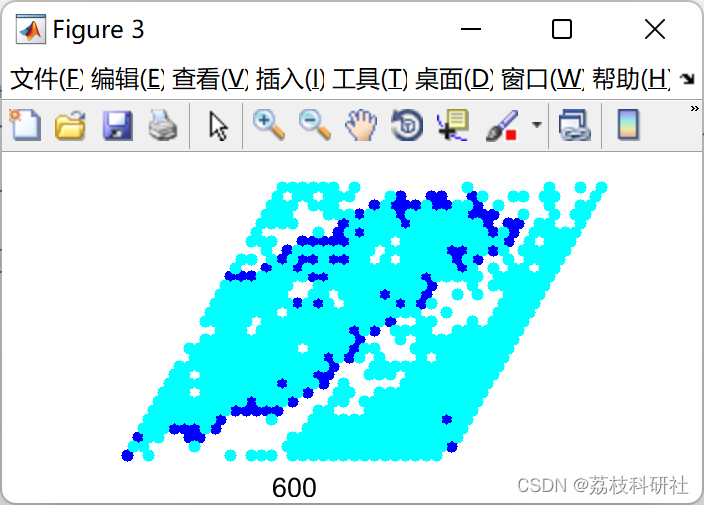
在包含模拟的图形窗口中，绘制了三种离散状态：激活或计划（蓝色）、
难熔性（浅蓝色）和静止/可兴奋（白色）。模拟的时间步长
编号显示在激活模式下方。要调制模拟的速度，请将输入参数更改为 pause 语句（在每个步骤中暂停的时间，以秒为单位）。

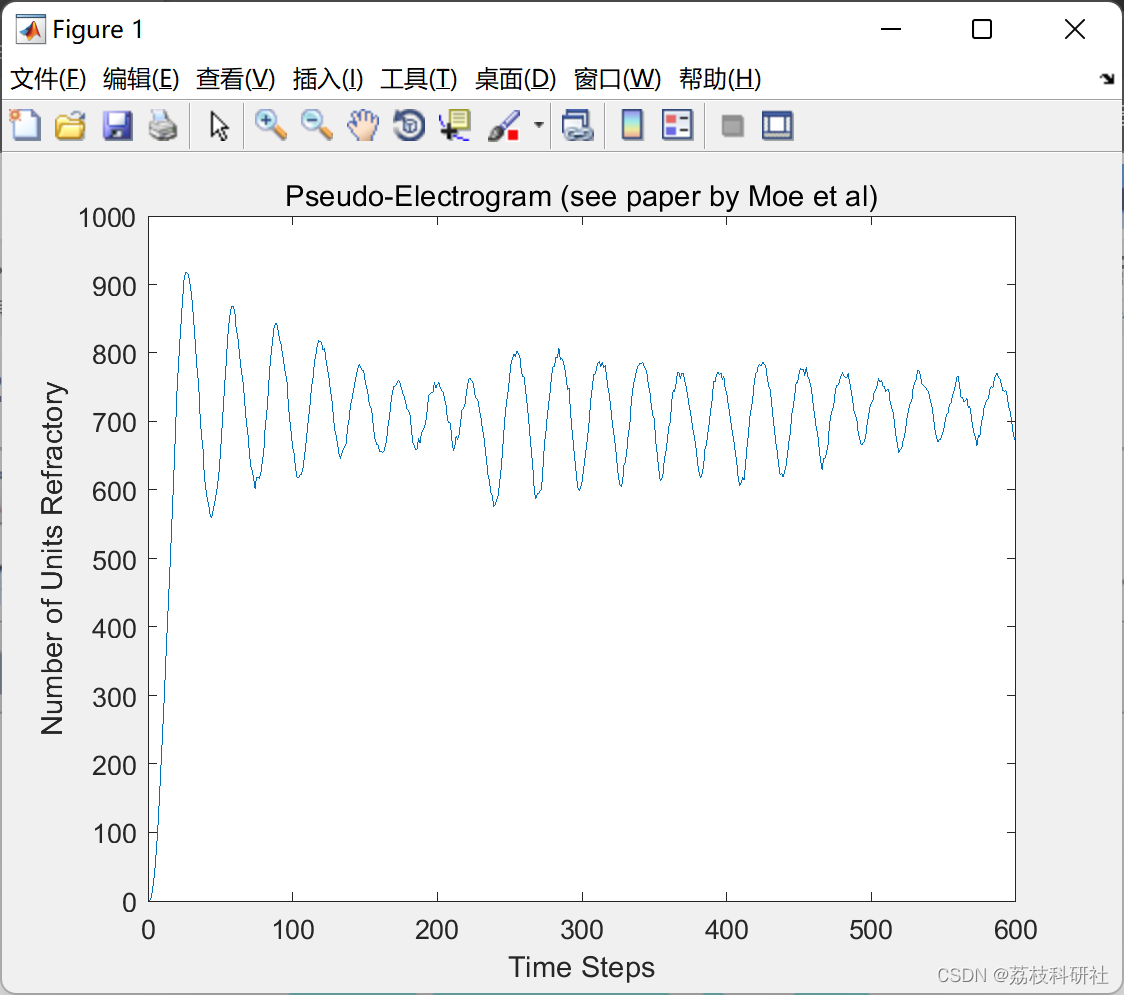
除了绘制整个表面上随时间变化的激活外，还生成了显示“伪电图”的第二个图。

📚2 运行结果

 

部分代码：

br=[1:31 1:31 zeros(1,34) 32*ones(1,34)];   % Row coordinates of border.
bc=[zeros(1,31) 33*ones(1,31) 0:33 0:33];   % Column coordinates of border.
px=0.5*(br-1)+bc; py=1+(br-1)*sqrt(3)/2;    % Convert coords to hexagonal for plotting.
fh=figure('position',[160 325 350 175],'color',[1 1 1]); % [160 325 630 330]
plot(px,py,'w.','markersize',16); hold on   % Plot the border.
axis image
axh=gca;
set(axh,'xcolor',[1 1 1],'ycolor',[1 1 1])
th=text(15,-2,'');

sr=[12 12 13 13]'; sc=[8 9 8 9]';       % Coordinates of units to stimulate.
si=sub2ind(size(s0),sr,sc);             % Indices of units in cluster to stimulate.
sched=[si ones(size(si))];                % Schedule the units to activate at step 1.
ph1=plot(-2,0,'b.','markersize',16);  % Create handles for active points.
ph2=plot(-2,0,'c.','markersize',16);  % Create handles for refractory points.
for step=1:600
   ia=sched(sched(:,2) == step,1);                % Indices into s0 to activate.
   ia2=sched(sched(:,2) > step,1);              % Additional indices into s0 to plot.
   [sy,sx]=ind2sub(size(s0),[ia;ia2]);          % Coordinates of activated units.
   px=0.5*(sy-1)+sx; py=1+(sy-1)*sqrt(3)/2;     % Convert coords to hexagonal for plotting.
   set(ph1,'xdata',px,'ydata',py);              % Update plot of active units.
   if step > 1
       [ry,rx]=ind2sub(size(s0),inz);               % Coordinates of refractory units.
       px=0.5*(ry-1)+rx; py=1+(ry-1)*sqrt(3)/2;     % Convert coords to hexagonal for plotting.
       set(ph2,'xdata',px,'ydata',py);              % Update plot of refractory units.
       drawnow
       pause(0.01)
       egram(step)=size(inz,1);                     % Build approx egram based on # of active units.
   end
   set(th,'string',num2str(step))                   % Update timer.
   
   s0=zeros(R,C); s0(ia)=1;                    % Update matrix of ones/zeros with activated units.
   sched(sched(:,2) == step,:)=[];          % Remove activated units from table.
   for j=1:size(ia,1)                       % Loop thru units acitvated at this step.
       atimes{ia(j)}=[atimes{ia(j)}; step]; % Append row of atimes with current step.
       if size(atimes{ia(j)},1) > 1         % Element has been activated at least twice.
           lastcycle=diff(atimes{ia(j)}(end-1:end)); %*dt;    % Previous interval (msec).
       else
           lastcycle=40;                    % Use default previous interval of 40 steps.
       end
       arp(ia(j))=round(k(ia(j))*sqrt(lastcycle));   % Set ref pd for units just active.
   end

   % Determine units to schedule for future activation.
   ins0=[];                                     % Indices of neighbors of active units.
   for jj=1:size(nhood,1)                        % Loop through nhood building column of neighbors.
      ins0=[ins0; find(matrixShift(s0,nhood(jj,1),nhood(jj,2)))];
   end
   if step < 80
       srp=arp(si);
       ins0=[ins0; si(srp<1)];
   end
   ins0=unique(ins0);                            % Exclude redundancies.
   ins0=setdiff(ins0,ia);                       % Exclude currently active elements.
   ins0=setdiff(ins0,sched(:,1));               % Exclude units already scheduled for activation.
   inz=find(arp > 0); ins0=setdiff(ins0,inz);   % Exclude units in state 1 (absolute refractory).
   ia2=intersect(ins0,find((arp == 0) | (arp == -1)));    % Units in state 2.
   sched=[sched;[ia2 step+4*ones(size(ia2))]];          % Schedule to activate in 4 steps.
   ia3=intersect(ins0,find((arp == -2) | (arp == -3)));    % Units in state 3.
   sched=[sched;[ia3 step+3*ones(size(ia3))]];          % Schedule to acivate in 3 steps.
   ia4=intersect(ins0,find((arp == -4) | (arp == -5)));    % Units in state 4.
   sched=[sched;[ia4 step+2*ones(size(ia4))]];          % Schedule to acivate in 2 steps.
   ia5=intersect(ins0,find(arp == -6));                    % Units in state 5 (completely recovered).
   sched=[sched;[ia5 step+ones(size(ia5))]];            % Schedule to acivate at next step.
   arp=max(-6,arp-1);                                   % Update refractory period.
end

figure; plot(egram);
title('Pseudo-Electrogram (see paper by Moe et al)')
xlabel('Time Steps')
ylabel('Number of Units Refractory')

% =================== Sub functions ===================
function out=matrixShift(m,r,c)

% MATRIXSHIFT Shift all elements of matrix m up by r rows and right
%   by c columns. Rows and/or columns of zeros are used to fill voids.

for k=1:abs(r)
   if r > 0, m=[m(2:end,:); zeros(1,size(m,2))];
   else m=[zeros(1,size(m,2)); m(1:end-1,:)];
   end
end

for k=1:abs(c)
   if c > 0, m=[zeros(size(m,1),1) m(:,1:end-1)];
   else m=[m(:,2:end) zeros(size(m,1),1)];
 

🌈3 Matlab代码实现

🎉4 参考文献

部分理论来源于网络，如有侵权请联系删除。

[1]American Heart Journal 1964; 67(2):200-220. 

[2]Peter Hammer (2022). Model of atrial fibrillation/flutter.