过了一遍第三章,大致理解了内容,认识了线性回归模型,对数几率回归模型,线性判别分析方法,以及多分类学习,其中有很多数学推理过程以参考他人现有思想为主,没有亲手去推。
术语学习
线性模型 linear model
非线性模型 nonlinear model
可解释性 comprehensibility
可理解性 understandability
线性回归 linear regression
均方误差 square loss
欧氏距离 Euclidean distance
最小二乘法 least square method
参数估计 parameter estimation
闭式 closed-form
多元线性回归 multivariate linear regression
满秩矩阵 full-rank matrix
正定矩阵 positive definite matrix
正则化 regularization
对数线性回归 log-linear regression
广义线性模型 generalized linear model
联系函数 link function
单位阶跃函数 unit-step function
替代函数 surrogate function
对数几率函数 logistic function
几率 odds
对数几率 log odds
对数几率回归 logistic regression
极大似然法 maximum likelihood method
对数似然 log-likelihood
梯度下降法 gradient descent method
牛顿法 Newton method
线性判别分析 Linear Discriminant Analysis
类内散度矩阵 within-class scatter matrix
类间散度矩阵 between-class scatter matrix
广义瑞利商 generalized Rayleigh quotient
迹 trace
分类器 classifier
拆分策略一对一 OvO One vs. One
一对其余 OvR One vs. Rest
多对多 MvM Many vs. Many
纠错输出码 ECOC Error Correcting Output Codes
编码矩阵 coding matrix
类别不平衡 class-imbalance
再缩放 rescaling
再平衡 rebalance
欠采样 undersampling
下采样 downsampling
过采样 oversampling
上采样 upsampling
阈值移动 threshold-moving
代价敏感学习 cost-sensitive learning
稀疏表示 sparse representation
稀疏性 sparsity
多标记学习 multi-label learning
3.1 试析在什么情形下式 (3.2) 中不必考虑偏置项 b.
可以理解的解释:
- f ( x ) = w i x i f(x)=w_{i}x_{i} f(x)=wixi始终经过原点,b=0,可以不考虑
- 考虑输出 f ( x ) f(x) f(x)和 x x x的变化关系时,不考虑
- 当两个线性模型相减时,消除了b。可用训练集中每个样本都减去第一个样本,然后对新的样本做线性回归,不用考虑偏置项b。
3.2 试证明,对于参数 ω,对率回归的目标函数 (3.18)是非凸的,但其对数似然函数 (3.27)是凸的.
对实数集上的函数,可通过求二阶导数来判别:若二阶导数在区间上非负,则称为凸函数;若二阶导数在区间上恒大于 0,则称为严格凸函数。
对率回归的目标函数 (3.18)是非凸的证明
式 3.18 ,其一阶导
∂
y
∂
w
=
x
(
y
−
y
2
)
\frac{\partial{y}}{\partial{w}}=x(y-y^{2})
∂w∂y=x(y−y2)
二阶导
∂
2
y
∂
w
∂
w
T
=
x
x
T
y
(
1
−
y
)
(
1
−
2
y
)
\frac{\partial^{2}{y}}{\partial{w}\partial{w^{T}}}=xx^{T}y(1-y)(1-2y)
∂w∂wT∂2y=xxTy(1−y)(1−2y)(即海森矩阵),
其中
x
x
T
xx^{T}
xxT 秩为1,非零特征值只有一个,其正负号取决于
y
(
1
−
y
)
(
1
−
2
y
)
y(1-y)(1-2y)
y(1−y)(1−2y) ,显然当
y
y
y在(0.5,1)之间变化时,特征值为负,于是3.18式关于
w
w
w 的海森矩阵非半正定,因此非凸。
对数似然函数 (3.27)是凸的证明参考南瓜书

3.3 编程实现对率回归,并给出西瓜数据集 3.0α 上的结果.
(待补充)
3.4 选择两个 UCI 数据集,比较 10 折交叉验证法和留 法所估计出的对率回归的错误率.
(待补充)
3.5 编辑实现线性判别分析,并给出西瓜数据集 3.0α 上的结果.
(待补充)
3.6 线性判别分析仅在线性可分数据上能获得理想结果?试设计一个改进方法,使其能较好地周于非线性可分数据
人们发展出一系列基于核函数的学习方法,统称为"核方法" (kernel methods). 最常见的,是通过"核化" (即引入核函数)来将线性学习器拓展为非线性学习器.下面我们以线性判别分析为例来演示如何通过核化来对其进行非线性拓展 7 从而得副"核线性判别分析" (Kernelized Linear Discriminant Analysis,简称 KLDA).
3.7 令码长为 9,类别数为 4,试给出海明距离意义下理论最优的 ECOC二元码井证明之.
“海明距离”是指两个码对应位置不相同的个数。
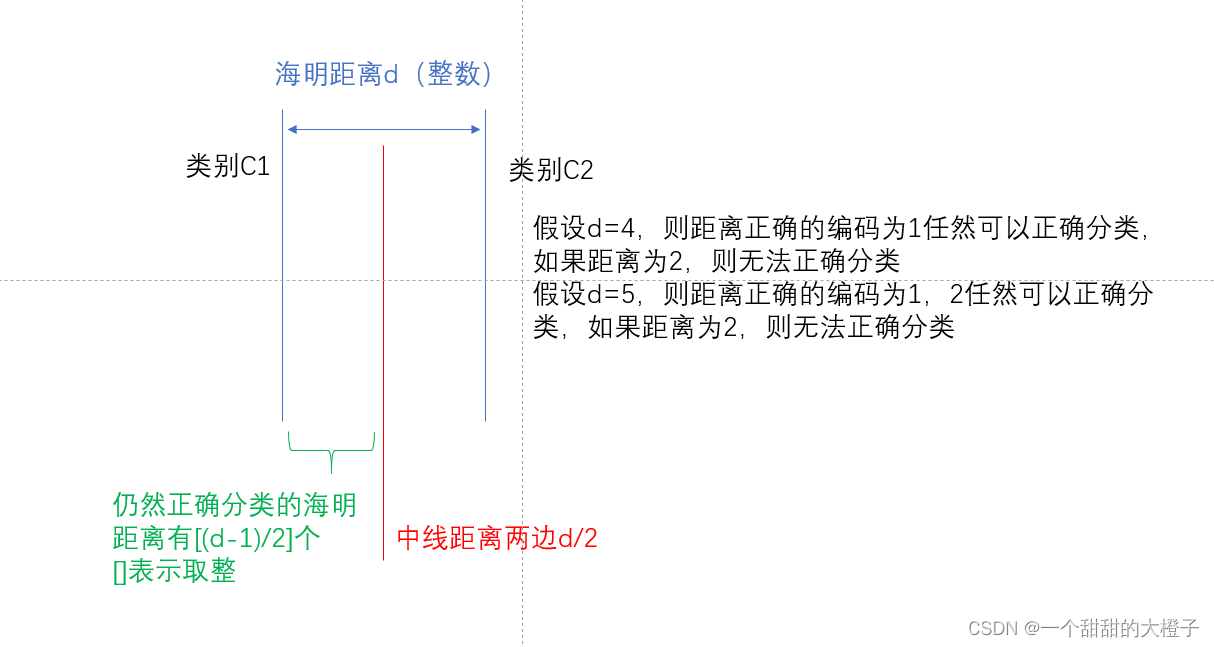
参考链接论文提到的,“假设任意两个类别之间最小的海明距离为 d ,那么此纠错输出码最少能矫正
[
d
−
1
2
]
\left[ \frac{d-1}{2} \right]
[2d−1] 位的错误。 可以用下图解释。
| – | f0 | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 |
|---|---|---|---|---|---|---|---|---|---|
| c1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| c2 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| c3 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| c4 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
参考链接1–解题
参考链接2–论文
3.8* ECOC 编码能起到理想纠错作用的重要条件是:在每一位编码上出错的概率相当且独立.试析多分类任务经 ECOC 编码后产生的二类分类器满足该条件的可能性及由此产生的影响.
西瓜书上标注的一句话
将多个类拆解为两个"类别子集”,不同拆解方式所形成的两个类别子集的区分难度往往不同,即其导致的二分类问题的难度不同;于是,一个理论纠错牲质很好、但导致的二分类问题较难的编码,与另一
个理论纠错性质差一些、但导致的二分类问题较简单的编码,最终产生的模型性能孰强孰弱很难说。
3.9 使用 OvR 和 MvM 将多分类任务分解为二分类任务求解时,试述为何无需专门针对类别不平衡性进行处理.
对 OvR 、 MvM 来说,由于对每个类进行了相同的处理,其拆解出的二分类任务中类别不平衡的影响会相互抵消,因此通常不需专门处理.
3.10* 试推导出多分类代价敏感学习(仅考虑基于类别的误分类代价)使用"再缩放"能获得理论最优解的条件.
参考链接1–解题