舵机驱动原理:

目前我所接触到的舵机，9g舵机，以及本文将要介绍的DS3115MG，它们作为舵机，一般接有三根线，其中俩根是供电使用，还有一根是信号线，供电需要我们对照产品手册选择合适的电源，而信号线则是重点学习的地方：

之前我有一篇文章讲过9g舵机的驱动：

MSP432学习笔记8：定时器A_PWM驱动舵机_NULL指向我的博客-CSDN博客

而我们今日学习的主角：DS3115MG，它的驱动原理与之大同小异，我们需要给信号线一个相应频率PWM的信号，让其知道有控制信号要到来，然后同时调整PWM的占空比即可调整其旋转角度

（这里信号的频率与占空比先不仔细说，后文会一起查阅介绍，手把手编程驱动）

这是舵机DS3115MG:

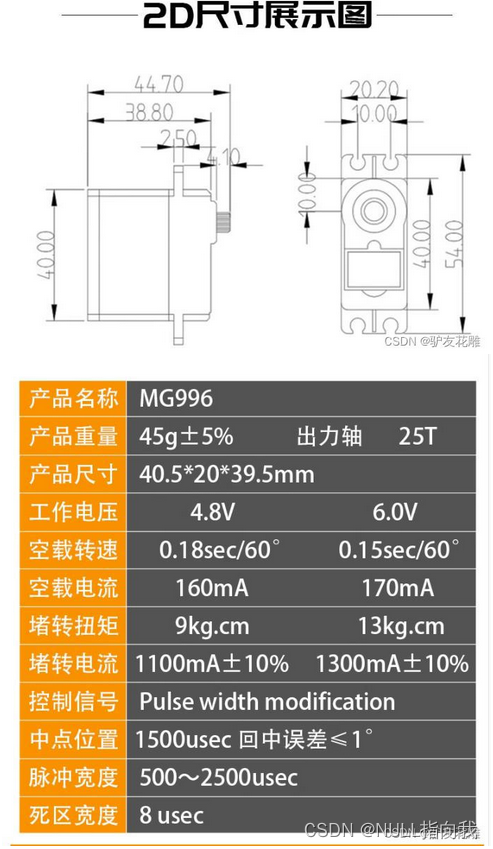
我们看到它的手册，挖掘有用信息：

我们需要知道的大致有三个重要点：1、电压电流 2、PWM频率 3、识别占空比范围

第一张图告诉我们，这个产品是有15KG的扭力的，而且预计可能要最大6V的供电：

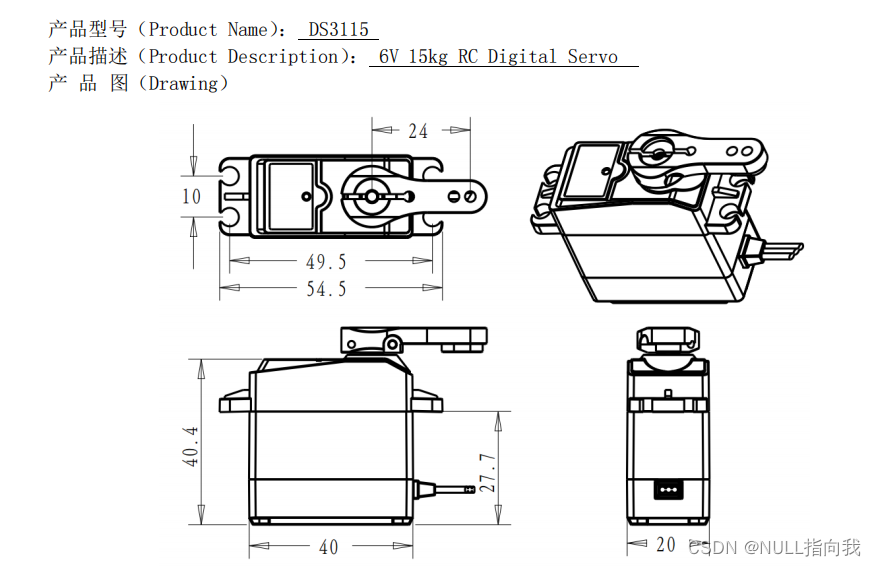
第二张图介绍基本机械特性与性能，使用机械电子产品应在合理的环境条件下

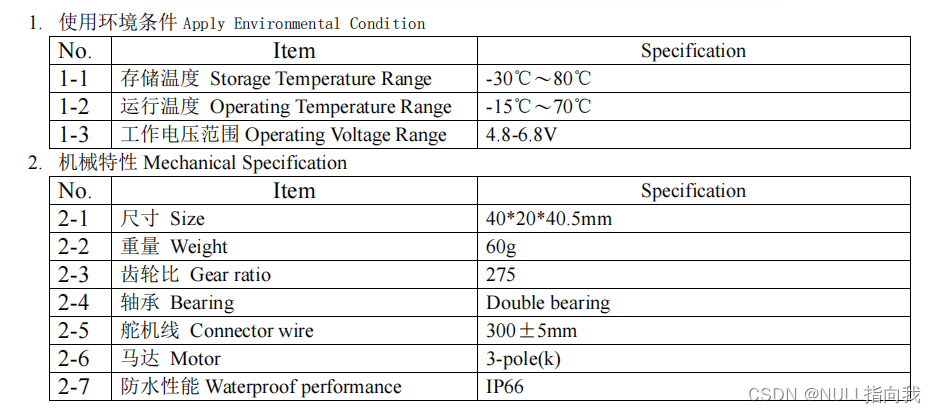
这张图便是有我们需要的参数：

1.PWM频率范围50~330Hz

2.脉宽范围是500~2500 us

3.精度是3us

4.旋转方向是顺时针

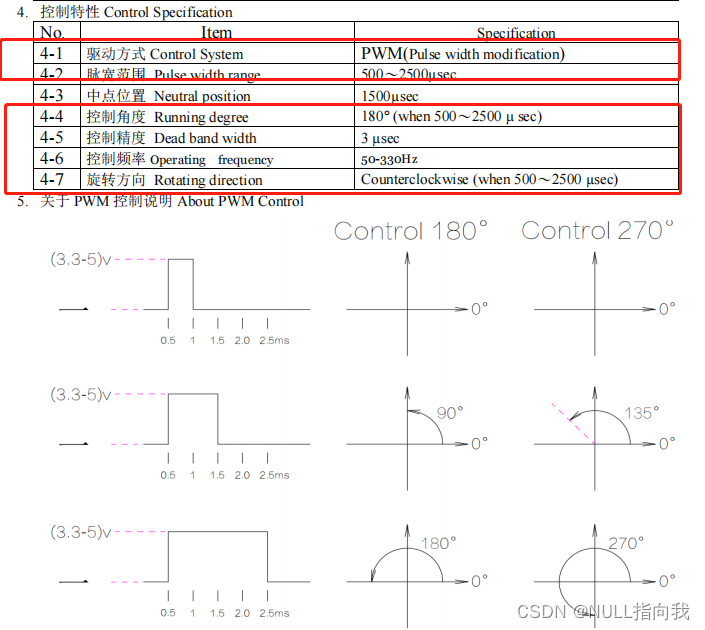
全角度反馈编程设计：

实验目标：

0.初始化定时器A的PWM模式

1.舵机缓慢从0~180全角度转动

2.反馈当前高电平占空比

首先我们有输出PWM的需求，因此这时少不了MSP432的定时器A，他作为瑞士军刀级别的多功能定时器模块，它有PWM输出的功能

初始化定时器TA3：

//定时器A3 PWM 初始化
void TimerA3_PWM_inint(void)
{
	//1.配置GPIO复用
	GPIO_setAsPeripheralModuleFunctionOutputPin(GPIO_PORT_P9,GPIO_PIN2,GPIO_PRIMARY_MODULE_FUNCTION);

	
	//2.配置结构体
	  Timer_A_PWMConfig TimA3_PWMConfig;																//定义一个名为 TimA1_PWMConfig的结构体
	  TimA3_PWMConfig.clockSource=TIMER_A_CLOCKSOURCE_SMCLK;						//时钟源
    TimA3_PWMConfig.clockSourceDivider=48;														//时钟分频 范围1~64
    TimA3_PWMConfig.timerPeriod=3333;																//自动重载值
    TimA3_PWMConfig.compareRegister=TIMER_A_CAPTURECOMPARE_REGISTER_3;//通道一（与引脚相关联）
    TimA3_PWMConfig.compareOutputMode=TIMER_A_OUTPUTMODE_TOGGLE_SET;	//输出模式
    TimA3_PWMConfig.dutyCycle=1;																		//此处可初始调占空比
	
	//初始化定时器：
	Timer_A_generatePWM(TIMER_A3_BASE,&TimA3_PWMConfig);
	
}

这段代码分为几个步骤来初始化定时器TA3：

1.配置GPIO复用

2.配置初始化结构体：

我此处的时钟源SMCLK是配置的48Mhz，48分频，

TimA3_PWMConfig.timerPeriod=3333; 是自动重载值，是根据需要频率计算的：

计算公式如下：

PWM频率 = 时钟源频率 / (（时钟源除数值“时钟分频”） *（CCR0值“自动重载值” + 1）)

此处我需要的是300HZ的信号，因此我的计算过程如下：

300=48 000 000/（48*（CCR0+1））

计算出CCR0约为3333

设计转角函数：

因为这个项目仅仅只需让这个舵机转就行了，所以这部分做的比较粗糙，使用了延时函数以及扔进主循环的诸多粗糙做法：

大致思路是定义好其最大与最小占空比，在定义其每次转角占空比增加的最小分度，让i从500~2500之间每次加三在变化，同时向上位机打印当前角度的i值：

#include "main.h"

#define DIV 3
#define DIV_MAX 2500
#define DIV_MIN 500

uint16_t i=0;

int main(void)
{
	  inint_all();   //初始化所有模块
    while (1)
    {
			if(i<DIV_MIN)
			{i=DIV_MIN;}
			i+=DIV;
			printf("%d\r\n",i);
			delay_ms(50);
			MAP_Timer_A_setCompareValue(TIMER_A3_BASE,TIMER_A_CAPTURECOMPARE_REGISTER_3,i);
			if(i>=DIV_MAX)
			{i=DIV_MIN;}
    }
}