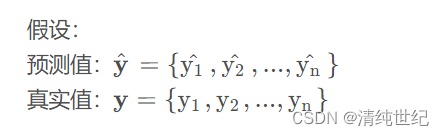
1、平均绝对误差

(MAE)Mean Absolute Error，是绝对误差的平均值，能更好地反映预测值误差的实际情况。范围[0,+∞)，当预测值与真实值完全吻合时等于0，即完美模型；误差越大，该值越大。

2、均方误差

MSE(mean-square error) 该统计参数是预测数据和原始数据对应点误差的平方和的均值。范围[0,+∞)，当预测值与真实值完全吻合时等于0，即完美模型；误差越大，该值越大。

3、均方根误差

均方根误差（Root Mean Square Error），其实就是MSE加了个根号，这样数量级上比较直观，比如RMSE=10，可以认为回归效果相比真实值平均相差10。范围[0,+∞)，当预测值与真实值完全吻合时等于0，即完美模型；误差越大，该值越大。

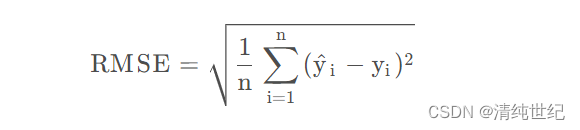
4、决定系数R2

决定系数R2(coefficient of determination)，也称判定系数或者拟合优度。它是表征回归方程在多大程度上解释了因变量的变化，或者说方程对观测值的拟合程度如何。拟合优度的有效性通常要求：自变量个数:样本数>1:10。

所以要想决定系数R2越接近1，必须满足MSE越小，也就是真实值与预测值相差不大，也就是模型拟合程度高，同时var方差越大，也就是我们的样本离散程度大，对应的我们实际采样过程中，就是要求样本是随机性，以及全面性，覆盖度广

注意：决定系数适用于线性回归，单变量或者多元线性；y=ax或者y=ax1+bx2…；拟合模型是非线性的，不能用决定系数来评价其拟合效果，例如：BP神经网络
当拟合程度不行，可以调整参数或者权重-例如a,b，使预测值与真实值越接近

5、方差

方差(variance)的计算公式：S2=1/n [(x1-X)2+(x2-X)2+(x3-X)2+…(xn-X)2] (X表示平均数）。
方差在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。概率论中方差用来度量随机变量和其数学期望（即均值）之间的偏离程度。

统计中的方差（样本方差）是每个样本值与全体样本值的平均数之差的平方值的平均数。在许多实际问题中，研究方差即偏离程度有着重要意义。

6、代码

直接调用：

#导入相应的函数库
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestRegressor
import numpy as np
import pandas as pd
         
#加载数据
data_url = "http://lib.stat.cmu.edu/datasets/boston"
raw_df = pd.read_csv(data_url, sep="s+", skiprows=22, header=None)
bos_house_data = np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :2]])
bos_house_target = raw_df.values[1::2, 2]

#建模分析
x_train,x_test,y_train,y_test = train_test_split(bos_house_data,bos_house_target,random_state=41)
forest_reg = RandomForestRegressor(random_state=41)
forest_reg.fit(x_train,y_train)
y_predict = forest_reg.predict(x_test)


# 使用sklearn调用衡量线性回归的MSE 、 RMSE、 MAE、r2
from math import sqrt
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score
print("mean_absolute_error:", mean_absolute_error(y_test, y_predict))
print("mean_squared_error:", mean_squared_error(y_test, y_predict))
print("rmse:", sqrt(mean_squared_error(y_test, y_predict)))
print("r2 score:", r2_score(y_test, y_predict))

#原生实现
# 衡量线性回归的MSE 、 RMSE、 MAE、r2
mse = np.sum((y_test - y_predict) ** 2) / len(y_test)
rmse = sqrt(mse)
mae = np.sum(np.absolute(y_test - y_predict)) / len(y_test)
r2 = 1-mse/ np.var(y_test) # 均方误差/方差
print(" mae:",mae,"mse:",mse," rmse:",rmse," r2:",r2)

自定义函数：

# 一般R、MAE、MAPE用的较多

# MAE计算
def mae(target, predict):
    return (abs(target-predict)).mean()
mae_val = mae(np.array(BH_old_data), np.array(BH_new_data))
mae_val_new = mae(np.array(BH_old_data), np.array(new_model_predict))

# MSE计算
def mse(target, predict):
    return ((target - predict)**2).mean()
mse_val = mse(np.array(BH_old_data), np.array(BH_new_data))
mse_val_new = mse(np.array(BH_old_data), np.array(new_model_predict))

# RMSE计算
def rmse(predictions, targets):
    return np.sqrt(((predictions - targets) ** 2).mean())
rmse_val = rmse(np.array(BH_old_data), np.array(BH_new_data))
rmse_val_new = rmse(np.array(BH_old_data), np.array(new_model_predict))

# R相关系数计算
def R(target, predict):
    SSR = sum((predict - (target).mean())**2)
    SST = sum((target - (target).mean())**2)
    return SSR/SST
r_val = R(np.array(BH_old_data), np.array(BH_new_data))
r_val_new = R(np.array(BH_old_data), np.array(new_model_predict))