1. NB 三人组介绍
1.1 快速排序(Quick Sort)
- 时间复杂度:
O(nlogn)

归位: 让元素去它该去的位置,保证左边的元素都比他小,右边都比他大;
1.1.1 原理图示:
假设初始列表:
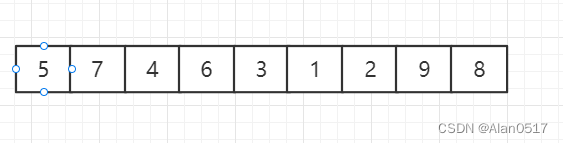
我们从左边第一个元素开始找,对5进行归位
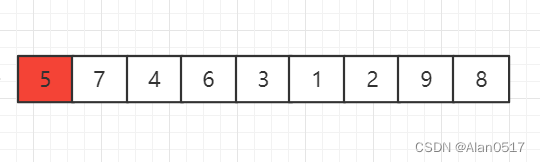
5归位之后,列表分为左右两部分,左边部分比5小,右边部分比5大,咱们先不关心 归位逻辑,接下来,咱们可以同时对两个列表进行归位操作,也就是对左边的2进行归位处理,对右边的6进行归位处理
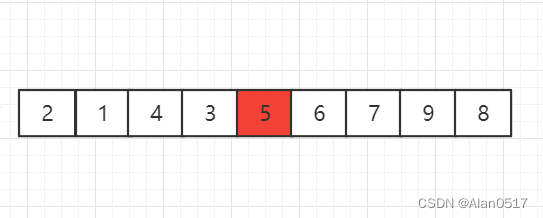
对左边的2进行归位,发现2左边只有1个元素,那2左边不需要排了,2右边有4和3两个元素的小列表,那么对4进行归位
对右边的6进行归位,因为6是最小的,所以右边部分分为两个列表,左边是0个元素,右边是 798
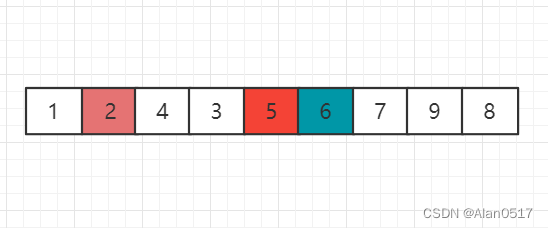
对4和3两个元素的小列表,左边的4进行归位后,4左边只有一个元素,右边0个元素,那么也就递归完了
对798列表的7进行归位,发现7也是最小的,7左边没有元素,右边是98元素,因此对98进行递归
接下来继续按列表归位
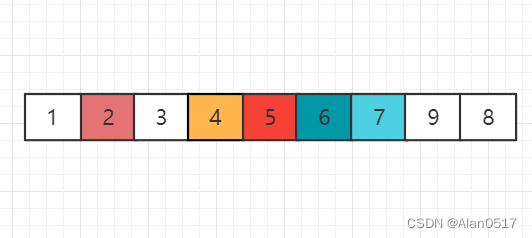
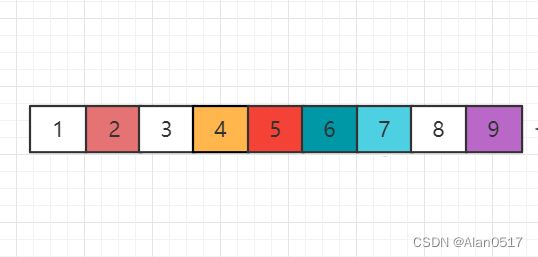
对98列表的9进行归位,递归完成后,9右边没有元素了,左边只有一个元素8,也就递归完成了
1.1.2 快速排序框架
/**
* 快速排序 框架
* <p>
* 思路:归位+递归
*
* @param arr 列表
* @param left 列表最左边元素下标
* @param right 列表最右边元素下标
*/
public void quickSort(int[] arr, int left, int right) {
//如果left< right,说明列表这个区域至少2个元素,2个或以上进行递归
if (left < right) {
//通过归位函数,找出归位的那个数的下标
int mid = partition(arr, left, right);
//对左边列表进行递归
quickSort(arr, left, mid - 1);
//对右边列表进行递归
quickSort(arr, mid + 1, right);
}
}
public int partition(int[] arr, int left, int right) {
//todo 归位逻辑
return -1;
}
1.1.3 归位逻辑 原理图
- 原始列表:

第一步,先将5存起来,这个时候我们发现列表最左边有一个空位,列表左边是存放比5小的数,右边是存放比5大的数,这个时候,我们可以从右边开始找比5小的数,存放在列表左边的空位上
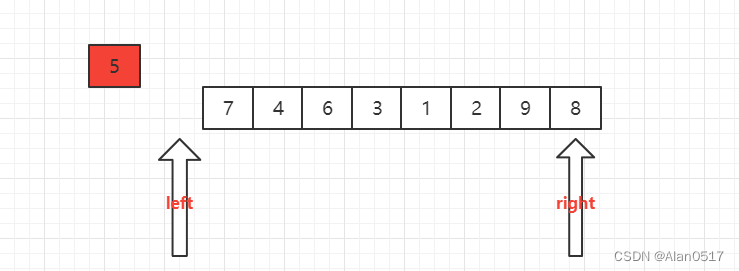
从右边开始找,找到2的时候发现,2比5小,于是把2放到左边的空位上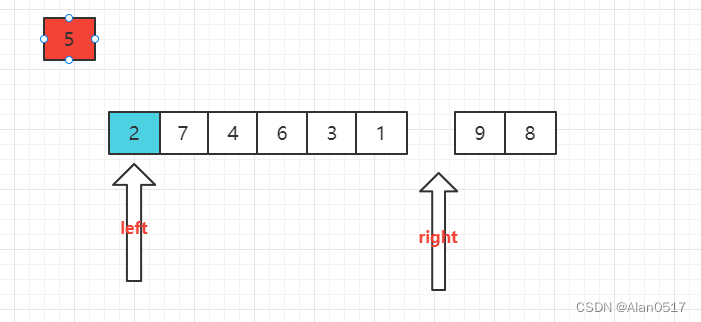
这个时候发现右边有一个空位,右边的空位是存放比5大的元素,于是从左边开始找比5大的元素放到右边的空位,找到是7,那么将7放到右边的空位,注意细节,是将left位置放到right位置
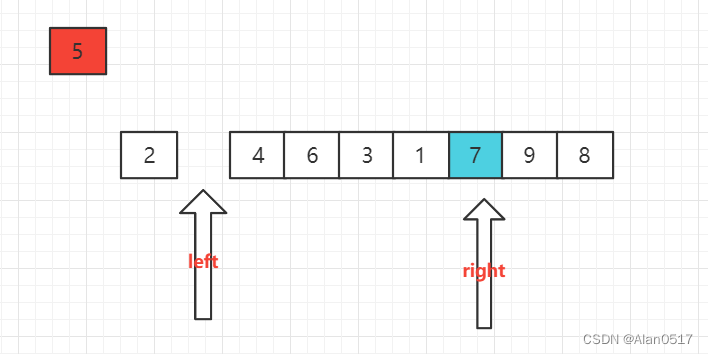
接下来 如法炮制
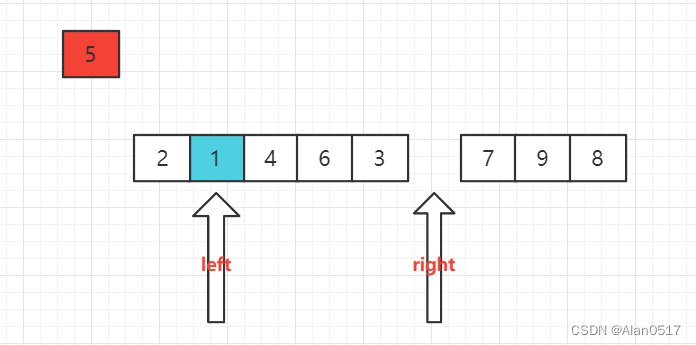
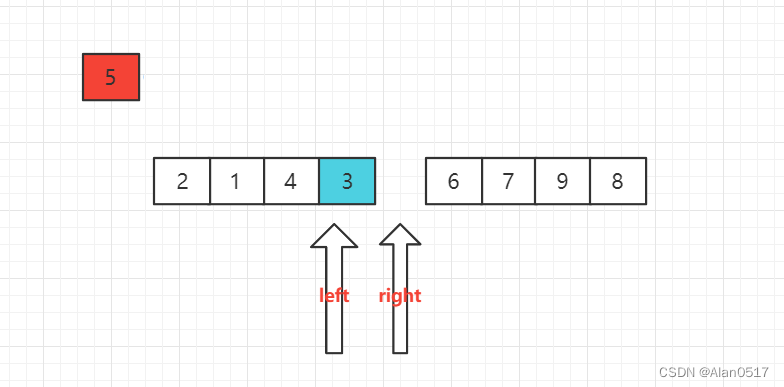
当left和right位置重合了说明位置就在中间了
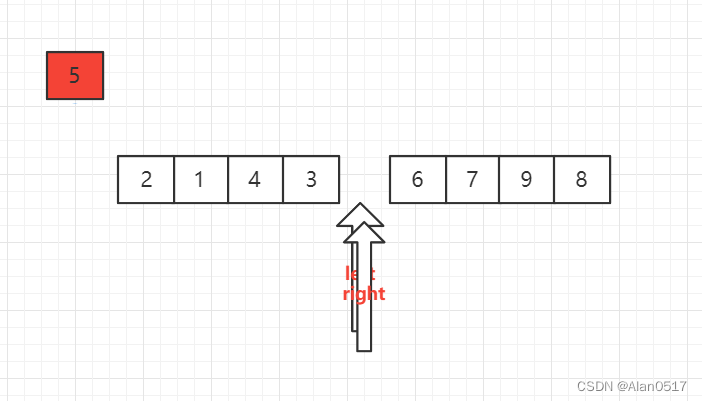
1.1.4 归位代码
public static int partition(int[] arr, int left, int right) {
//将第一个数暂存起来,用于比较
int tmp = arr[left];
//当left=right时,表示中间位置,归位就结束了
while (left < right) {
//从右边开始找,如果这个数大于tmp,则right往左边移动一位
while (left < right & arr[right] >= tmp) {
right -= 1;
}
//如果这个数找到了,则将右边的值写到左边的空位上
arr[left] = arr[right];
// System.out.println("arr = " + Arrays.toString(arr) + " => right");
//从左边开始找,如果这个数小于tmp,则left往右边移动一位
while (left < right & arr[left] <= tmp) {
left += 1;
}
//如果这个数找到了,则将左边的值写到右边的空位上
arr[right] = arr[left];
// System.out.println("arr = " + Arrays.toString(arr) + " => left");
}
//将tmp归位
arr[left] = tmp;
//返回 mid的值,此时left和right是重合的,所以返回left和right都一样
return left;
}
1.1.5 快速排序的 最终代码
import java.util.Arrays;
/**
* 快速排序
*
* @author wql
* @date 2022/12/10 10:15
*/
public class QuickSort {
public static void main(String[] args) {
int[] arr = {5, 7, 4, 6, 3, 1, 2, 9, 8};
System.out.println("arr = " + Arrays.toString(arr));
quickSort(arr, 0, arr.length - 1);
System.out.println("arr = " + Arrays.toString(arr));
}
/**
* 快速排序 框架
* <p>
* 思路:归位+递归
*
* @param arr 列表
* @param left 列表最左边元素下标
* @param right 列表最右边元素下标
*/
public static void quickSort(int[] arr, int left, int right) {
//如果left< right,说明列表这个区域至少2个元素,2个或以上进行递归
if (left < right) {
//通过归位函数,找出归位的那个数的下标
int mid = partition(arr, left, right);
//对左边列表进行递归
quickSort(arr, left, mid - 1);
//对右边列表进行递归
quickSort(arr, mid + 1, right);
}
}
public static int partition(int[] arr, int left, int right) {
//将第一个数暂存起来,用于比较
int tmp = arr[left];
//当left=right时,表示中间位置,归位就结束了
while (left < right) {
//从右边开始找,如果这个数大于tmp,则right往左边移动一位
while (left < right & arr[right] >= tmp) {
right -= 1;
}
//如果这个数找到了,则将右边的值写到左边的空位上
arr[left] = arr[right];
// System.out.println("arr = " + Arrays.toString(arr) + " => right");
//从左边开始找,如果这个数小于tmp,则left往右边移动一位
while (left < right & arr[left] <= tmp) {
left += 1;
}
//如果这个数找到了,则将左边的值写到右边的空位上
arr[right] = arr[left];
// System.out.println("arr = " + Arrays.toString(arr) + " => left");
}
//将tmp归位
arr[left] = tmp;
//返回 mid的值,此时left和right是重合的,所以返回left和right都一样
return left;
}
}
1.1.6 快速排序时间复杂度分析
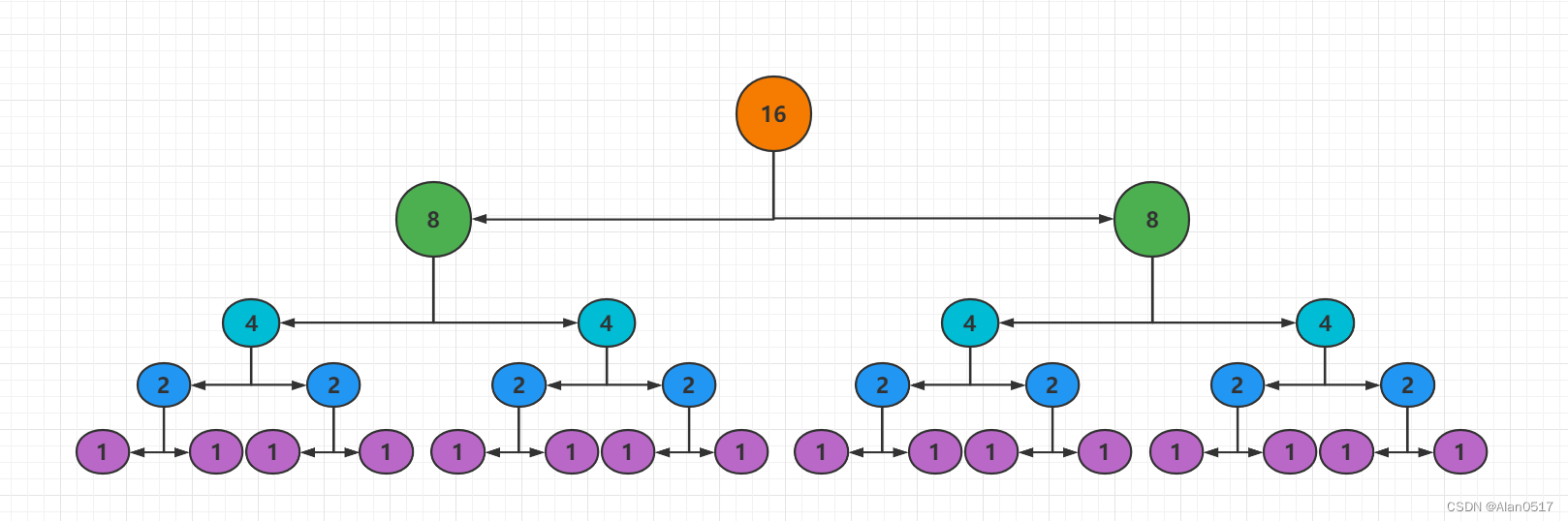
不严谨的推导:假设现在16个数,第一次分成8+8,16拆分成8+8 是第一次归位操作,第二次2个8又拆分为2组4+4,也就是2次归位操作,第三次2组4+4又拆分为4组2+2,也就是四次归位操作,再然后4组2+2又拆分为8组1+1,也就是8组归位操作,而每一次归位操作时间复杂度都是O(n),不管是进行1次归位还是8次,时间复杂度都是O(n),所以每一层的时间复杂度是O(n),目前n是16,一共是log216层,也就是4层,那对于n来说,就是log2n层,简写logn层,所以快速排序的时间复杂度就是O(nlogn)
1.1.7 快速排序存在的问题
- 当列表是倒叙的,比如int[] arr ={9,8,7,6,5,4,3,2,1}, 这种情况是最坏的情况,因为它每次归位只少1个数,这样递归就是n次,因为他的时间复杂度是O(n^2), 要想解决这个问题很简单,以往我们每次都是将列表的最左边的第一个数作为第一个需要归位的数,那么我们可以随机从列表里面取一个数,和列表的最左边的第一个数交换位置,随机化,这样最坏情况的概率会很小,后面的逻辑和上面快速排序的一样,这样就可以最大避免这个问题;
1.2 堆排序(Heap Sort)
- 时间复杂度:
O(nlogn)
1.2.1 树的概念简介
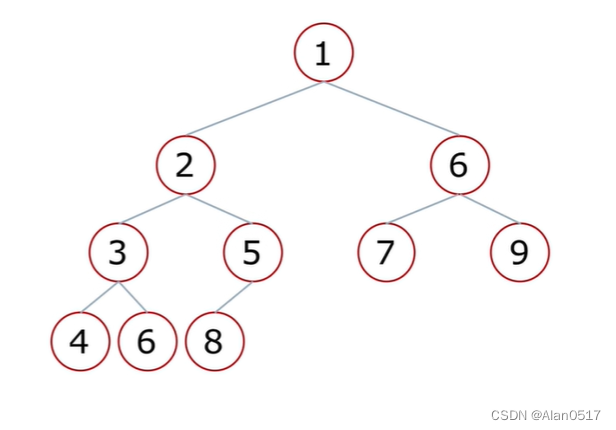
- 树是一种数据结构 比如:目录结构
- 树是一种可以递归定义的数据结构
- 树是由n个节点组成的集合:
- 如果n=0,那么这就是一颗空树;
- 如果n>0,那存在一个节点作为树的根节点,其他节点可以分为m个集合,每个集合本身又是一棵树;
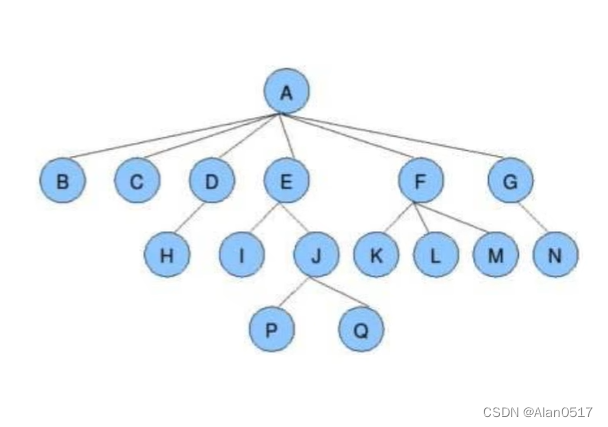
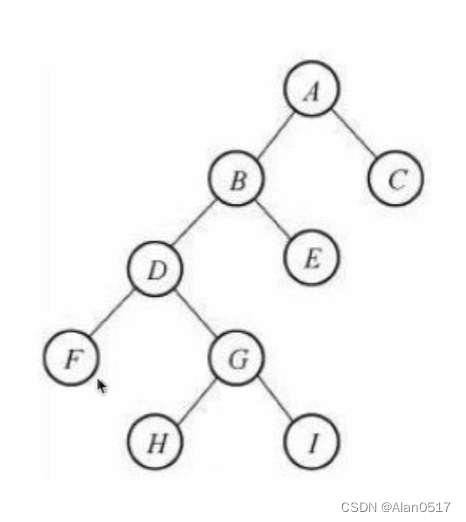
如果上图倒过来看,它就是一棵树;
- 树的一些概念:
- 根节点,叶子节点
- A就是它的根节点,不能分叉的节点是叶子节点,比如BHPQN
- 树的深度(高度)
- 如上图所示,一共4层,那么树的深度是4
- 树的度
- 分叉最多的数量,比如A,它下面有6个叉,也是这棵树最多的分叉,那么树的度就是6
- 孩子节点/父节点
- 节点之间的关系:比如E是A的孩子节点,而E是J的父节点
- 子树
- 如果把ESJP 拆出来,就是一颗子树,比如你从树上掰下来一个分支,那就是子树
- 根节点,叶子节点
1.2.2 二叉树
- 度 不超过 2的树
- 每个节点最多有2个孩子节点
- 两个孩子节点被区分为左孩子节点和右孩子节点
1.2.3 完全二叉树
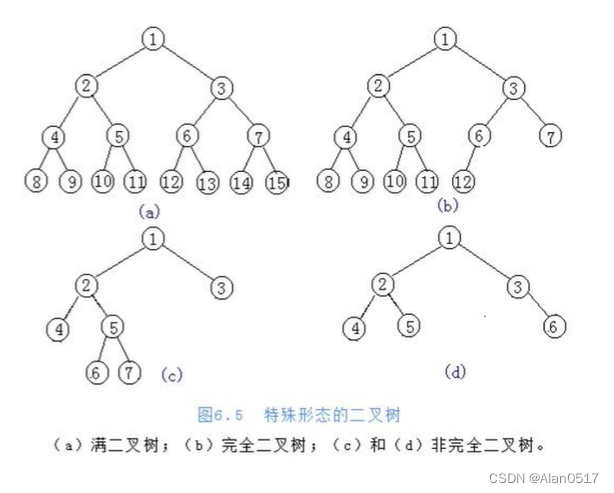
- 满二叉树:一个二叉树,如果每一层的节点数达到最大值,则这个二叉树就是满二叉树;
- 完全二叉树:叶节点只能出现再最下层和次下层,并且最下面一层的节点都集中在该层最左边的若干位置的二叉树;可以理解为 最后一层可以不满,但是必须从左依次排过来,也可以理解是从满二叉树最后一层的右边拿走几个数;
- 非完全二叉树: 基于完全二叉树,但是第二层又少了几个节点
1.2.4 二叉树的存储方式(表示方式)
- 链式存储方式
- 顺序存储方式
- 简单来说就是列表存储
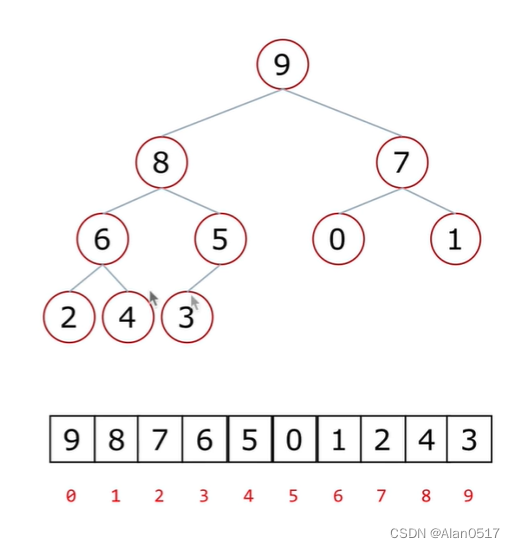
- 父节点和左孩子节点的编号下标有什么关系?
- 0-1 1-3 2-5 3-7 4-9
- 总结就是:
- 父找子: i -> 2i+1
- 子找父: i -> (i-1) /2 整除
- 父节点和右孩子节点的编号下标有什么关系?
- 0-2 1-4 2-6 3-8 4-10
- 总结就是:
- 父找子: i -> 2i+2
- 子找父: i -> (i-1) /2 整除
1.2.5 堆排序-简单介绍
- 什么是堆?
- 堆:一种特殊的完全二叉树结构
- 大根堆:一颗完全二叉树,满足任一节点都比其他孩子节点大;
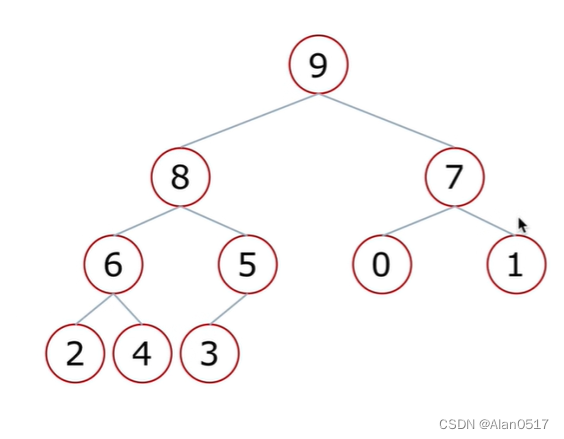
- 小根堆:一颗完全二叉树,满足任一节点都比其他孩子节点小;
1.2.6 堆排序-向下调整性质
- 假设根节点的左右子树都是堆,但根节点不满足堆的性质;
- 可以通过一次向下的调整来将淇变成一个堆;
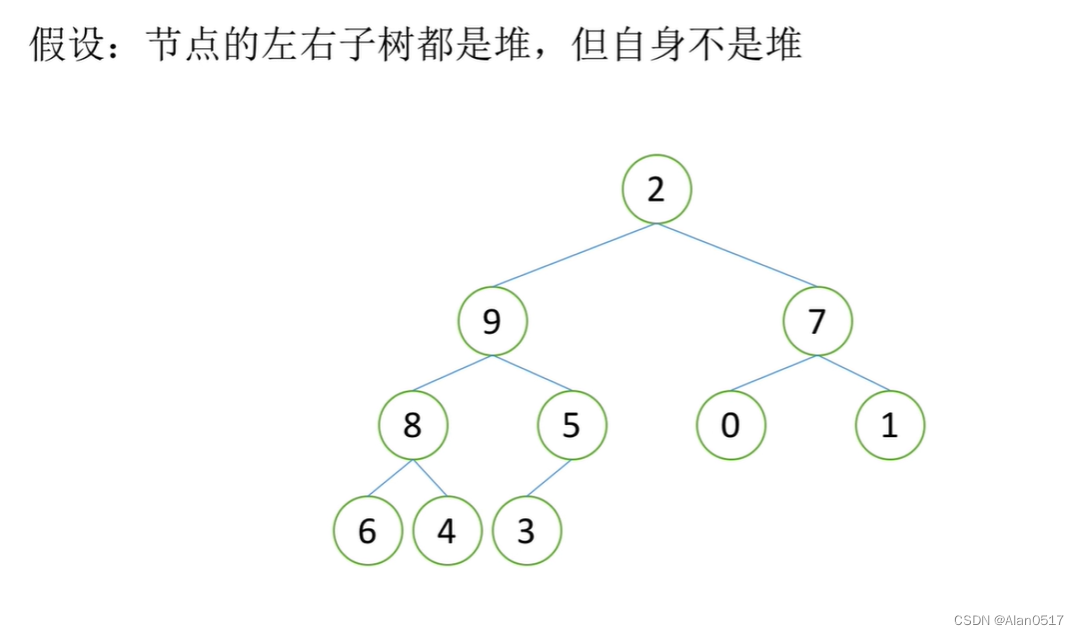
如上图所示,它既不是大根堆也不是小根堆;
向下调整 代码:
/**
* 堆向下调整排序
* <p>
* 父找子
* j=i*2+1 (i是父)
*
* @param arr 列表
* @param low 堆的根节点 下标位置
* @param high 堆的最后一个元素的下标位置
*/
public static void sift(int[] arr, int low, int high) {
//i 表示最开始指向根节点 指针,也就是父节点
int i = low;
//j最开始表示i左孩子的节点
int j = 2 * i + 1;
// tmp表示最开始的堆顶元素,需要暂存起来,用于后续比较
int tmp = arr[low];
//当j的下标大于堆的最后一个元素的下标时,表示此时的i没有孩子节点了,循环终止
while (j <= high) {
//如果右孩子存在且比左孩子大
if (j + 1 <= high & arr[j + 1] > arr[j]) {
//j的指针此时指向右孩子
j = j + 1;
}
//如果子孩子此时比tmp大
if (arr[j] > tmp) {
//则要换位置,将孩子与父亲交换位置
arr[i] = arr[j];
//同时指针向下移动一层
i = j;
j = 2 * i + 1;
} else {
//如果tmp更大,表示子节点小于tmp,tmp可以当爸爸,所以将tmp放在i的位置即可
arr[i] = tmp;
break;
}
}
//如果没有子节点了,则直接将tmp放在叶子节点上即可
arr[i] = tmp;
}
1.2.7 堆排序-构建堆
如果当前不是堆,那么需要先构建堆,再向下调整排序,然后取堆顶元素;
如下图所示,构建堆,从列表最后一个叶子节点开始,自下而上寻找,子找父,也就是
i=(j-1)/2 整除
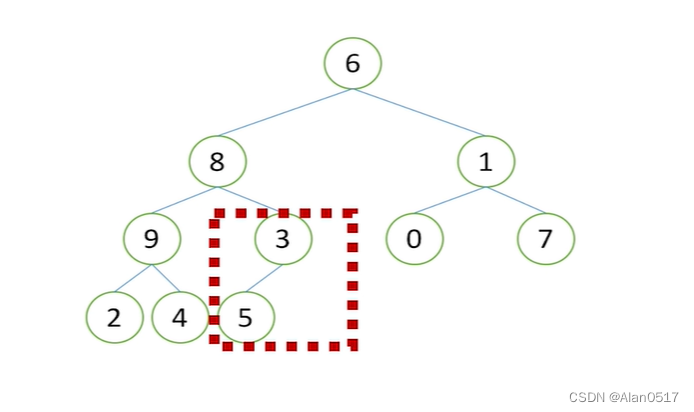
代码如下:
/**
* 建堆
*
* @param arr 列表
*/
public static void buildHeap(int[] arr) {
int length = arr.length;
//由于建堆是子找父,所以是 i=(j-1)/2,而子节点最后的位置是n-1,且倒叙
for (int i = (length - 2) / 2; i > -1; i--) {
sift(arr, i, length - 1);
}
}
1.2.8 堆排序过程
- 建立堆
- 得到堆顶元素,为最大元素
- 去掉堆顶,将堆最后一个元素放到堆顶,此时可通过一次调用重新使堆有序
- 堆顶元素为第二大元素
- 重复第二步,直到堆变空;
如图所示:
- 假设现在是一个堆(大根堆)
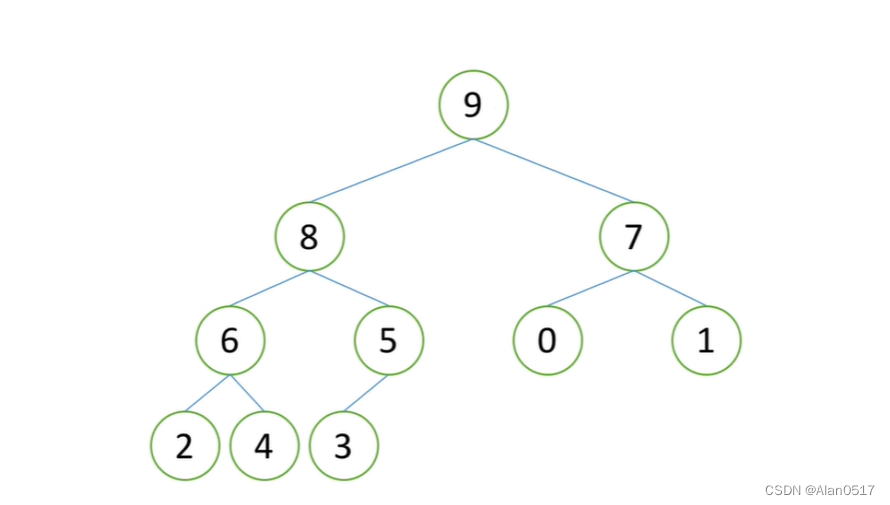
1, 堆顶一定是最大元素,此时把9拿走,堆顶就空了,这个时候我们把最后一个元素3放上去
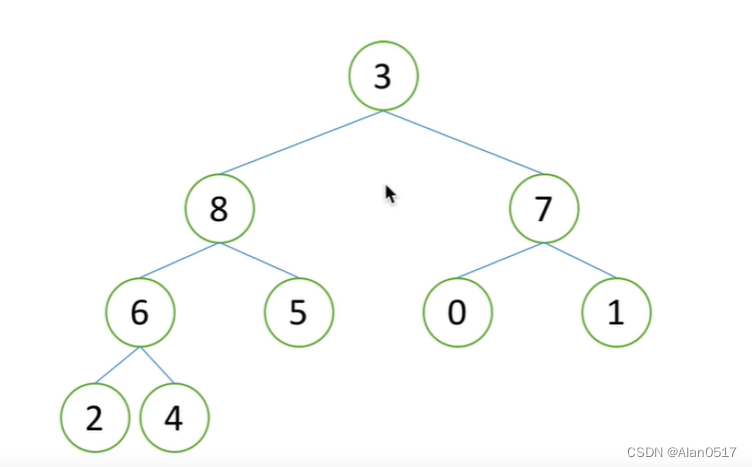
当3放上去之后,就满足了堆向下调整的性质,调整完之后,第二大的元素就出来了,也就是8;
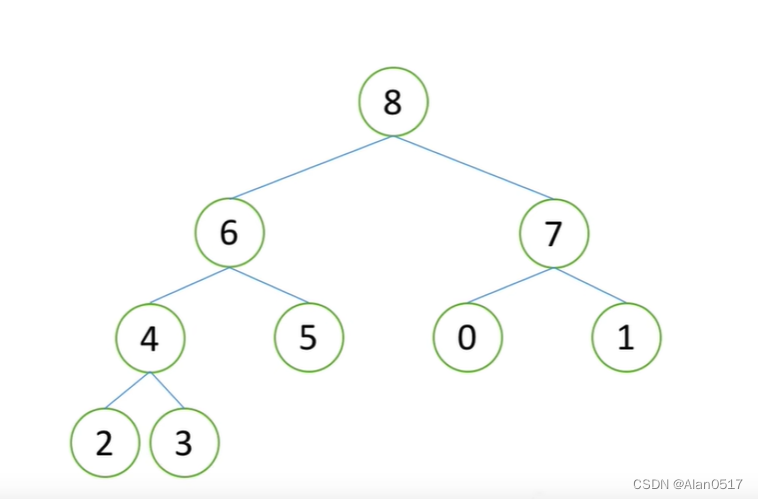
依次类推,通过堆顶挨个出数,一个有序列表就出来了;
所以堆排序的顺序是:构建堆->挨个出数
完整代码如下:
import java.util.Arrays;
/**
* 堆排序
*
* @author wql
* @date 2022/12/10 17:15
*/
public class HeapSort {
public static void main(String[] args) {
int[] arr = {5, 7, 4, 6, 3, 1, 2, 9, 8};
System.out.println("arr = " + Arrays.toString(arr));
handHeapSort(arr);
System.out.println("arr = " + Arrays.toString(arr));
}
public static void handHeapSort(int[] arr) {
//建堆
buildHeap(arr);
//挨个出数
for (int i = arr.length - 1; i > 0; i--) {
//i 指向当前堆的最后一个元素,将堆顶的元素与最后一个元素做交换,继续排序
int tmp = arr[0];
arr[0] = arr[i];
arr[i] = tmp;
sift(arr, 0, i - 1);
}
}
/**
* 建堆
*
* @param arr 列表
*/
public static void buildHeap(int[] arr) {
int length = arr.length;
//由于建堆是子找父,所以是 i=(j-1)/2,而子节点最后的位置是n-1,且倒叙
for (int i = (length - 2) / 2; i > -1; i--) {
sift(arr, i, length - 1);
}
}
/**
* 堆向下调整排序
* <p>
* 父找子
* j=i*2+1 (i是父)
*
* @param arr 列表
* @param low 堆的根节点 下标位置
* @param high 堆的最后一个元素的下标位置
*/
public static void sift(int[] arr, int low, int high) {
//i 表示最开始指向根节点 指针,也就是父节点
int i = low;
//j最开始表示i左孩子的节点
int j = 2 * i + 1;
// tmp表示最开始的堆顶元素,需要暂存起来,用于后续比较
int tmp = arr[low];
//当j的下标大于堆的最后一个元素的下标时,表示此时的i没有孩子节点了,循环终止
while (j <= high) {
//如果右孩子存在且比左孩子大
if (j + 1 <= high & arr[j + 1] > arr[j]) {
//j的指针此时指向右孩子
j = j + 1;
}
//如果子孩子此时比tmp大
if (arr[j] > tmp) {
//则要换位置,将孩子与父亲交换位置
arr[i] = arr[j];
//同时指针向下移动一层
i = j;
j = 2 * i + 1;
} else {
//如果tmp更大,表示子节点小于tmp,tmp可以当爸爸,所以将tmp放在i的位置即可
arr[i] = tmp;
break;
}
}
//如果没有子节点了,则直接将tmp放在叶子节点上即可
arr[i] = tmp;
}
}
1.2.9 堆排序时间复杂度分析
- 堆排序里面核心是 sift函数, 如下图所示,它的时间复杂度是logn,因为它是父找子,是个折半的过程;

再看完整的 堆排序,所以堆排序的时间复杂度是 O(nlogn)

1.2.10 堆排序-topk问题
假设现在有n个数,设计算法得到前k大的数(k<n)
场景:假设现在微博热搜取前100,n的基数是一亿;
解决思路:
- 排序后切片,那么如果选择排序算法的话,分析一波
- 快速排序/堆排序 O(nlogn)
- 排序LowB三人组 O(kn)
- 分析发现 LowB三人组的时间复杂度的更低;
- 最优解,使用堆排序思路: O(nlogk)
- 解决思路:
- 取列表前k个元素建立一个小根堆。堆顶就是目前第k大的数。
- 依次向后遍历原列表,对于列表中的元素,如果小于堆顶,则忽略该元素;如果大于堆顶,则将堆顶更换为该元素,并且对堆进行一次调整;
- 遍历列表所有元素后,倒序弹出堆顶;
代码如下:
小根堆,向下排序
/**
* 堆向下调整排序(小根堆)
* <p>
* 父找子
* j=i*2+1 (i是父)
* <p>
* 小根堆
*
* @param arr 列表
* @param low 堆的根节点 下标位置
* @param high 堆的最后一个元素的下标位置
*/
public static void siftSmall(int[] arr, int low, int high) {
//i 表示最开始指向根节点 指针,也就是父节点
int i = low;
//j最开始表示i左孩子的节点
int j = 2 * i + 1;
// tmp表示最开始的堆顶元素,需要暂存起来,用于后续比较
int tmp = arr[low];
//当j的下标大于堆的最后一个元素的下标时,表示此时的i没有孩子节点了,循环终止
while (j <= high) {
//如果右孩子存在且比左孩子小
if (j + 1 <= high & arr[j + 1] < arr[j]) {
//j的指针此时指向右孩子
j = j + 1;
}
//如果子孩子此时比tmp小
if (arr[j] < tmp) {
//则要换位置,将孩子与父亲交换位置
arr[i] = arr[j];
//同时指针向下移动一层
i = j;
j = 2 * i + 1;
} else {
//如果tmp更大,表示子节点小于tmp,tmp可以当爸爸,所以将tmp放在i的位置即可
arr[i] = tmp;
break;
}
}
//如果没有子节点了,则直接将tmp放在叶子节点上即可
arr[i] = tmp;
}
topk代码:
public static int[] topK(int[] arr, int k) {
//1.取前k个数作为小根堆
int[] heap = Arrays.copyOfRange(arr, 0, k);
//2.将取出来的k个数的数组建堆
for (int i = (k - 2) / 2; i > -1; i--) {
siftSmall(heap, i, k - 1);
}
//3.查看从k开始到数组n-1的位置的元素与k数组堆顶的关系
for (int i = k; i < arr.length - 1; i++) {
//如果这个数大于heap堆顶的数
if (arr[i] > heap[0]) {
//将值替换堆顶的数
heap[0] = arr[i];
//向下排序
siftSmall(heap, 0, k - 1);
}
}
//4.挨个出数: 到这一步,现在heap里面的数已经是前k大的数了
for (int i = k - 1; i > 0; i--) {
int tmp = heap[0];
heap[0] = heap[i];
heap[i] = tmp;
siftSmall(heap, 0, i - 1);
}
return heap;
}
测试:
public static void main(String[] args) {
int[] arr = new int[]{1, 9, 2, 4, 5, 8, 3};
System.out.println("ints = " + Arrays.toString(arr));
int[] ints = topK(arr, 3);
System.out.println("ints = " + Arrays.toString(ints));
}
1.3 归并排序(Merge Sort)
- 时间复杂度:
O(nlogn)
1.3.1 什么叫归并?
- 假设现在的列表分两段有序,如何将其合成为一个有序列表?
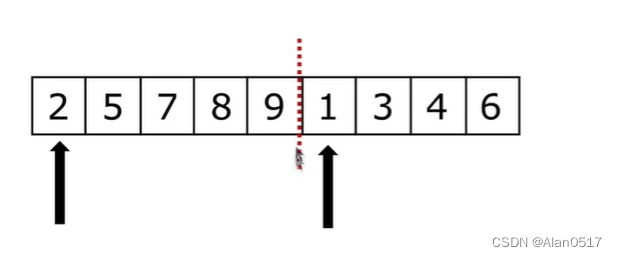
如上所示,合成的这种操作称为归并;
原理图如下所示:
- 虚线将两个列表分开,两个箭头分别指向的是列表的第一个
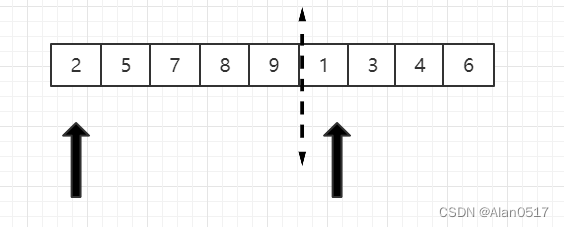
- 将两边的第一个元素相比较,1更小,则将1拿出来,1对应的原来的指针向右移动一位
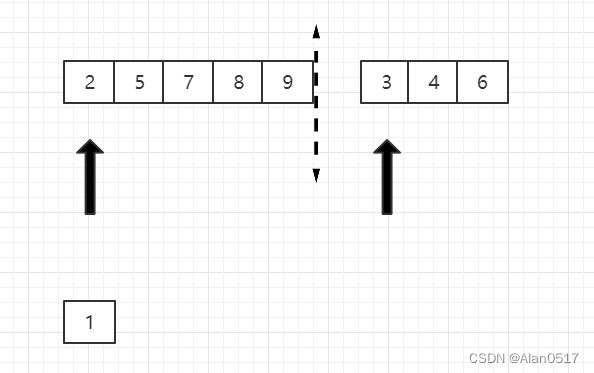
- 然后将2和3比,2小,2出来,指向2的指针向右移动一位
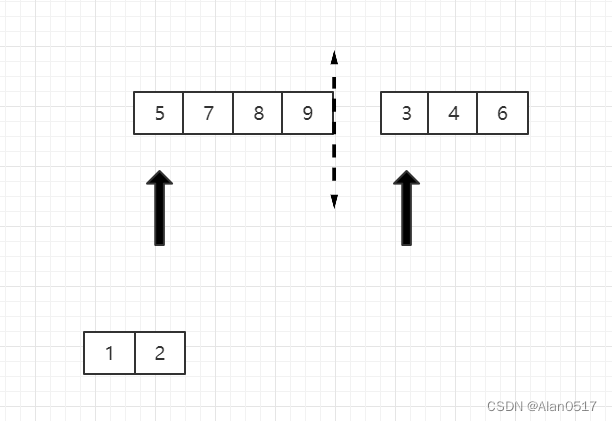
- 然后将5和3比,3小,3出来,指向3的指针向右移动一位
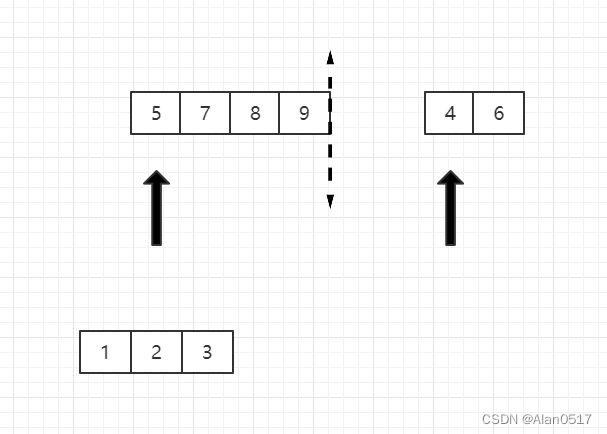
- 然后将5和4比,4小,4出来,指向4的指针向右移动一位
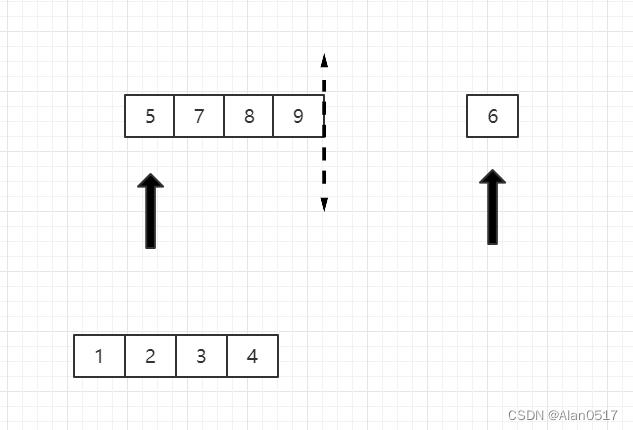
- 然后将5和6比,5小,5出来,指向5的指针向右移动一位
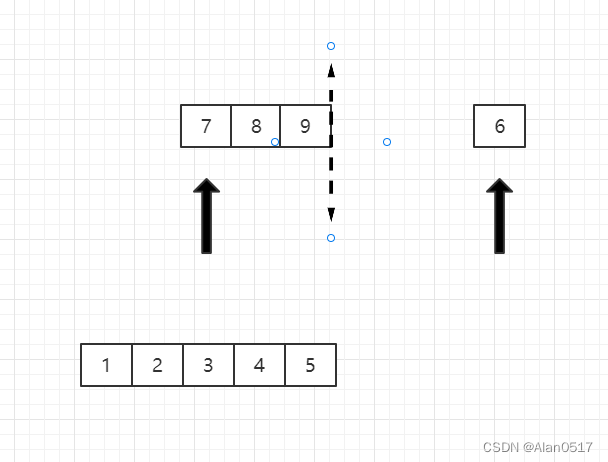
- 然后将7和6比,6小,6出来,此时发现右边那列已经没有数了,则后面只需要将左边的依次放入即可
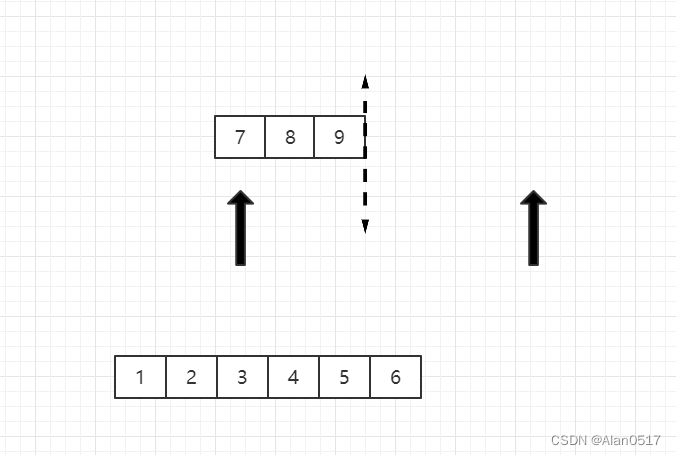
- 然后将7和6比,6小,6出来,此时发现右边那列已经没有数了,则后面只需要将左边的依次放入即可;
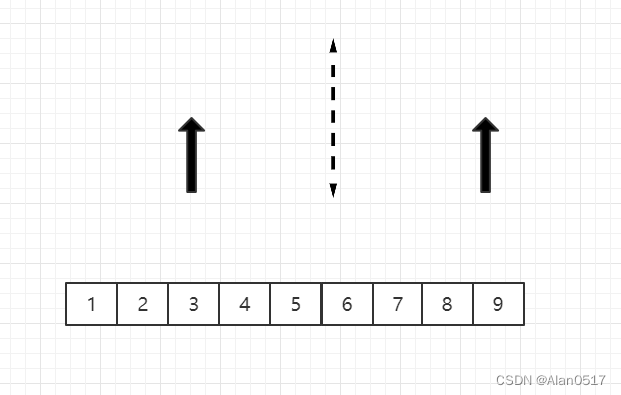
1.3.2 归并代码
public class MergeSort {
public static void main(String[] args) {
Integer[] arr = {4, 7, 8, 9, 1, 2, 3, 5};
System.out.println("arr = " + Arrays.toString(arr));
merge(arr, 0, 3, arr.length - 1);
System.out.println("arr = " + Arrays.toString(arr));
}
/**
* 归并
*
* @param arr 合列表
* @param low 合列表最左边第一个下标位置
* @param mid 合列表虚线位置(左边列表最后一个位置)
* @param high 合列表最右边的位置
*/
public static void merge(Integer[] arr, int low, int mid, int high) {
//左边列表指针位置
int i = low;
//右边列表指针位置
int j = mid + 1;
//临时列表
List<Integer> temp = new ArrayList<>();
//只有当两边列表都有数时
while (i <= mid && j <= high) {
//当左边列表第一个元素小于右边列表第一个元素
if (arr[i] < arr[j]) {
//将更小的那个放入临时列表中
temp.add(arr[i]);
//同时指针向右移动一位
i += 1;
} else {
temp.add(arr[j]);
//同时指针向右移动一位
j += 1;
}
}
//当上面第一个while执行完之后,两个列表肯定有一个没数了
//如果左边没有数,这个while是不会执行的,下面两个while只会执行一个
while (i <= mid) {
//将更小的那个放入临时列表中
temp.add(arr[i]);
//同时指针向右移动一位
i += 1;
}
while (j <= mid) {
//将更小的那个放入临时列表中
temp.add(arr[j]);
//同时指针向右移动一位
j += 1;
}
//重新将值赋回列表
for (int i1 = low; i1 < temp.size(); i1++) {
arr[i1] = temp.get(i1);
}
}
}
1.3.3 归并排序思想
- 分解:将列表越分越小,直至分成一个元素;
- 终止条件:一个元素是有序的;
- 合并:将两个有序列表归并,列表越来越大;
如下图所示:先分解后合并
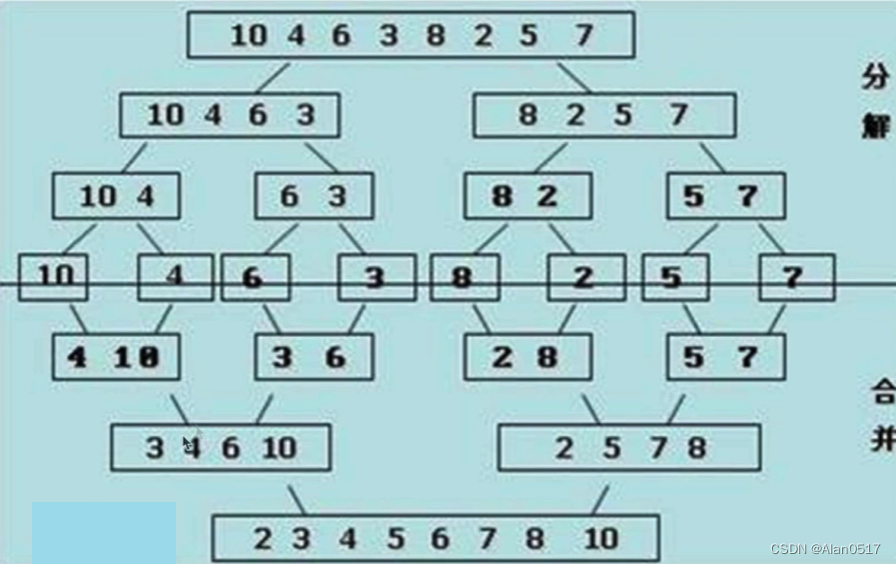
1.3.4 归并排序代码
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
/**
* 归并排序
*
* @author wql
* @date 2022/12/10 23:57
*/
public class MergeSort {
public static void main(String[] args) {
Integer[] arr = {4, 7, 8, 9, 1, 2, 3, 5};
System.out.println("arr = " + Arrays.toString(arr));
mergeSort(arr, 0, arr.length - 1);
System.out.println("arr = " + Arrays.toString(arr));
}
/**
* 归并
*
* @param arr 合列表
* @param low 合列表最左边第一个下标位置
* @param mid 合列表虚线位置(左边列表最后一个位置)
* @param high 合列表最右边的位置
*/
public static void merge(Integer[] arr, int low, int mid, int high) {
//左边列表指针位置
int i = low;
//右边列表指针位置
int j = mid + 1;
//临时列表
List<Integer> temp = new ArrayList<>();
//只有当两边列表都有数时
while (i <= mid && j <= high) {
//当左边列表第一个元素小于右边列表第一个元素
if (arr[i] < arr[j]) {
//将更小的那个放入临时列表中
temp.add(arr[i]);
//同时指针向右移动一位
i += 1;
} else {
temp.add(arr[j]);
//同时指针向右移动一位
j += 1;
}
}
//当上面第一个while执行完之后,两个列表肯定有一个没数了
//如果左边没有数,这个while是不会执行的,下面两个while只会执行一个
while (i <= mid) {
//将更小的那个放入临时列表中
temp.add(arr[i]);
//同时指针向右移动一位
i += 1;
}
while (j <= mid) {
//将更小的那个放入临时列表中
temp.add(arr[j]);
//同时指针向右移动一位
j += 1;
}
//重新将值赋回列表
for (int i1 = low; i1 < temp.size(); i1++) {
arr[i1] = temp.get(i1);
}
}
/**
* 归并排序
*
* @param arr 列表
* @param low 列表最左边第一个下标位置
* @param high 列表最右边的位置
*/
public static void mergeSort(Integer[] arr, int low, int high) {
//如果low小于high,说明至少有两个元素,递归
if (low < high) {
int mid = (low + high) / 2;
//左边列表排序
mergeSort(arr, low, mid);
//右边列表排序
mergeSort(arr, mid + 1, high);
//归并
merge(arr, low, mid, high);
}
}
}
综上:归并是O(n),递归是logn,所以时间复杂度一共是log(nlogn),空间复杂度O(n)
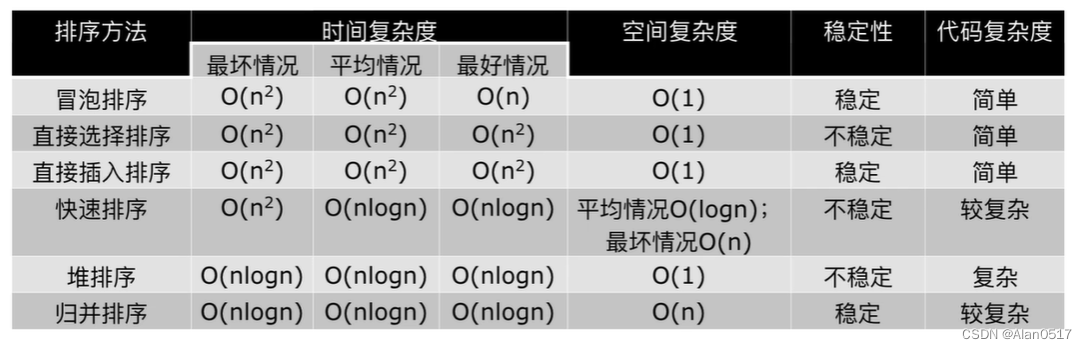
2. NB三人组小总结
- 三种排序算法的时间复杂度都是O(nlogn)
- 一般情况下,就运行时间而言(快速排序最快)
- 快速排序 < 归并排序 < 堆排序
- 三种排序算法的缺点:
- 快速排序: 极端情况下排序效率低;
- 倒序的情况时间复杂度达到O(n^2),但是可以随机化解决这个问题
- 归并排序:需要额外的内存开销;
- 堆排序:在快的排序算法中相对较慢 ;
- 快速排序: 极端情况下排序效率低;
备注说明:
- 如果使用到递归,其实会使用系统栈的空间,函数会一层一层走,每走一层消费O(1)空间;
- 稳定性:当两个值相等时,保证他们的相对位置不变;
- 比如 {name:“a”, age:10} {name:“b”, age:12} {name:“a”, age:14} 三个排序,排完之后是这样 {name:“a”, age:10} {name:“a”, age:14} {name:“b”, age:12} ,b变了,但是前面2个a的相对位置不变,这种就是稳定性
- 上面的排序都是交换排序,
只要是挨着交换的,都是稳定的,因为只要他们一样,就不交换,如果是飞来飞去换的,跳着换的,那就是不稳定的;