完全背包--动态规划

news2024/9/26 5:20:40

一)模板题:完全背包

【模板】完全背包_牛客题霸_牛客网 (nowcoder.com)

第一问:

一)定义一个状态表示:

dp[i][j]表示从前i个物品中选，总体积不超过j，所有选法中，最大的价值

二)根据状态标识推到状态转移方程:根据最后一个位置的状态来划分问题

之前做01背包问题的时候我们i位置的值是可以选也是可以不选的，但是在多重背包里面，最有一个位置的值可以不选，可以选择1个，可以选择2个，还可以选择多个，所以说此时可以进行讨论的情况就变得非常多，只要背包能放得下，那么我就可以无限选

1)如果我进行挑选i位置的礼物1个，那么我们只需要去0到i-1区间内去寻找j-v[i]的最大价值即可，if(j-v[i]>=0) dp[i][j]=dp[i-1][j-v[i]]+w[i](你所进行挑选的礼物不能超过j)

2)如果我们挑选i位置的礼物2个，那么我们只需要去找0-i-1区间去寻找j-2v[i]的礼物的最大价值即可，if(j-2*v[i]>=0) dp[i][j]=dp[i-1][j-2v[i]]+2*w[i]；

3)如果挑选i位置的礼物3个，dp[i][j]=dp[i-1][j-3v[i]+2*w[i]；

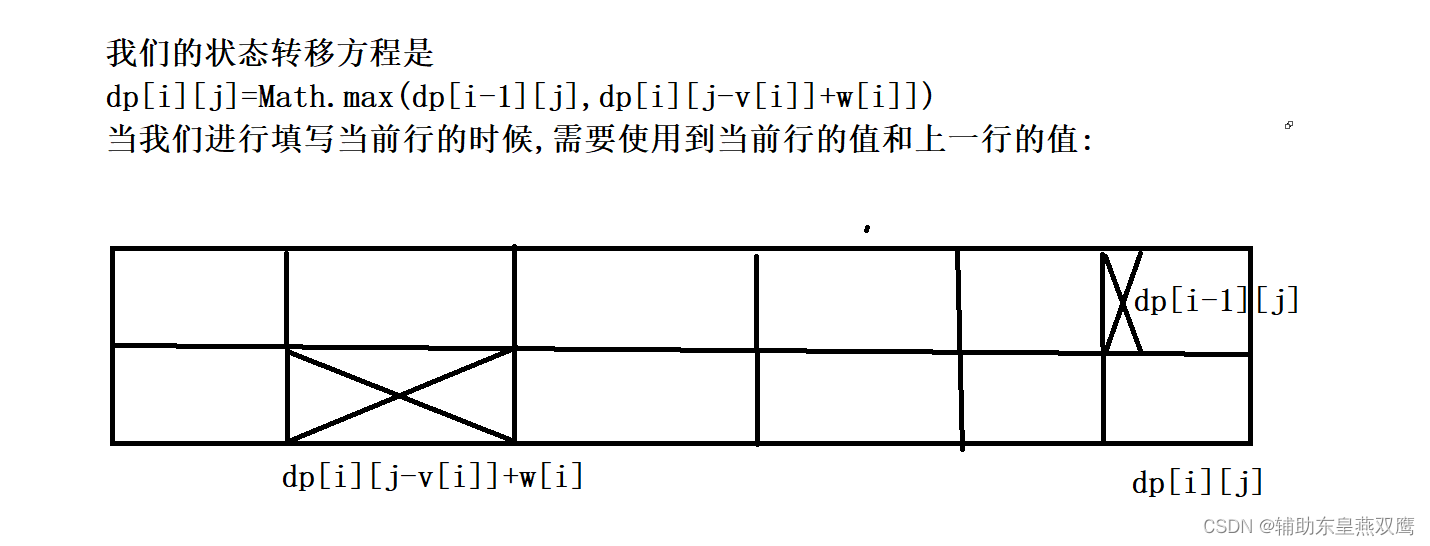
所以最终的状态转移方程就是dp[i][j]=Math.max(dp[i-1][j]，dp[i-1][j-k*v[i]]+k*w[i])

上面的状态转移方程的终极状态就是j-kv[i]和j-xv[i]要无限接近等于0，所以k=x

三)初始化:

我们这个题是新增加了一行，新增加了一列

dp[0][0]=0

dp[0][i]=0(什么都不选，体积为0，价值为0)

dp[i][0]=0

其实这个初始化的时候是不需要考虑第一列的时候，j此时等于0，那么j-v[i]>=0，那么v[i]也只能等于0，那么此时dp[i][j-v[i]]=dp[i][0]+w[i]，此时只会使用到上一行的值，此时和j一点关系都没有，所以第一行不用初始化

四)填表顺序:

这个题就和01背包问题的填表顺序不一样了，01背包问题是使用的是全部是上一行的状态，而完全背包问题使用的是上一行的状态和右边的状态，所以最终的填表顺序就是从上向下每一行只能从左向右，所以返回值就是dp[n][V]

第二问:

这一问和上一问不同的是总体积一定要装满，也就是说最终的总体机之和一定要等于V

一)定义一个状态标识:

dp[i][j]表示从前i个物品中进行选择，总体积恰好等于j，所有选择方法中，礼物的最大价值

二)根据状态表示推到状态转移方程

1)如果不选择i位置的商品，那么我就去前i-1中选择物品的体积等于j的所有的商品组合中的最大值，dp[i][j]=dp[i-1][j]，但是有可能会出现无法在前i-1个商品中选择的商品组合中恰好商品的总体积之和等于j的情况，所以我们约定dp[i][j]=-1表示无法在前i-1个商品中选择的商品组合中恰好等于j的情况

2)如果选择i位置的商品，当前商品我可以选择1个，也可以选择2个，只要当前背包装得下，况且说背的总体积等于j即可

dp[i][j]=Math.max(dp[i-1][j]，dp[i-1][j-v[i]]+w[i])

j-v[i]>=0&&dp[i-1][j-v[i]]!=-1(无法在i-1个商品中选择商品体积要等于j-v[i]的值的组合

三)初始化

dp[0][0]=0

dp[0][i]=-1(无法在前0个商品中选择礼物的总体积是i的情况)

dp[i][0]=0

四)填表顺序+返回值:从上到下，每一行必须从左向右
import java.util.Scanner;

// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
    public static void main(String[] args) {
       Scanner scanner=new Scanner(System.in);
       int n=scanner.nextInt();
       int V=scanner.nextInt();
       int[] v=new int[n+1];
       int[] w=new int[n+1];
       int[][] dp1=new int[n+1][V+1];
       for(int i=1;i<=n;i++){
         v[i]=scanner.nextInt();
         w[i]=scanner.nextInt();
       }
    for(int i=1;i<=n;i++){
    for(int j=1;j<=V;j++){
            dp1[i][j]=dp1[i-1][j];
if(j-v[i]>=0) dp1[i][j]=Math.max(dp1[i][j],dp1[i][j-v[i]]+w[i]);
         }
       }
    System.out.println(dp1[n][V]);
    int[][] dp2=new int[n+1][V+1];
    dp2[0][0]=0;
    for(int i=1;i<=V;i++){
        dp2[0][i]=-1;
      }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=V;j++){
    if(j-v[i]>=0&&dp2[i][j-v[i]]!=-1) 
            dp2[i][j]=dp2[i][j-v[i]]+w[i];
    else dp2[i][j]=-1;//如果无法选择出那么dp[i][j]=-1
    dp2[i][j]=Math.max(dp2[i][j],dp2[i-1][j]);
        }
      }
       System.out.println(dp2[n][V]==-1?0:dp2[n][V]);
    }
}

利用滚动数组来做空间上的优化:

所以说现在能不能使用一行来完成滚动数组的优化？

当然可以但是填表顺序一定要从左向右进行填表

import java.util.Scanner;

// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
    public static void main(String[] args) {
       Scanner scanner=new Scanner(System.in);
       int n=scanner.nextInt();
       int V=scanner.nextInt();
       int[] v=new int[n+1];
       int[] w=new int[n+1];
       int[] dp1=new int[V+1];
       for(int i=1;i<=n;i++){
         v[i]=scanner.nextInt();
         w[i]=scanner.nextInt();
       }
    for(int i=1;i<=n;i++){
    for(int j=1;j<=V;j++){
if(j-v[i]>=0) dp1[j]=Math.max(dp1[j],dp1[j-v[i]]+w[i]);
         }
       }
    System.out.println(dp1[V]);
    int[] dp2=new int[V+1];
    dp2[0]=0;
    for(int i=1;i<=V;i++){
        dp2[i]=-1;
      }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=V;j++){
    int temp=dp2[j];
    if(j-v[i]>=0&&dp2[j-v[i]]!=-1) 
            dp2[j]=dp2[j-v[i]]+w[i];
    else dp2[j]=-1;//如果无法选择出那么dp[i][j]=-1
    dp2[j]=Math.max(temp,dp2[j]);
        }
      }
       System.out.println(dp2[V]==-1?0:dp2[V]);
    }
}